Was ist latin hypercube sampling?

Beim lateinischen Hypercube-Sampling handelt es sich um eine Methode, mit der Zufallszahlen abgetastet werden können, bei denen die Stichproben gleichmäßig über einen Stichprobenraum verteilt sind.

Es wird häufig zur Generierung von Stichproben verwendet, die als kontrollierte Zufallsstichproben bezeichnet werden, und wird häufig in der Monte-Carlo-Analyse eingesetzt, da es die Anzahl der für die Erzielung genauer Ergebnisse erforderlichen Simulationen erheblich reduzieren kann.

Beispielhafte Einführung

Um die Idee des lateinischen Hypercube-Samplings zu verstehen, betrachten Sie das folgende einfache Beispiel:

Angenommen, wir möchten eine Stichprobe von 2 Werten aus einem normalverteilten Datensatz mit einem Mittelwert von 0 und einer Standardabweichung von 1 erhalten.

Wenn wir zum Erhalten dieser Stichprobe einen echten Zufallszahlengenerator verwenden, ist es möglich, dass beide Werte größer als 0 oder beide Werte kleiner als 0 sind.

Wenn wir jedoch das lateinische Hypercube-Sampling verwenden würden, um diese Stichprobe zu erhalten, wäre garantiert, dass ein Wert größer als 0 und ein anderer kleiner als 0 wäre, da wir den Stichprobenraum gezielt in einen Bereich mit Werten größer als 0 unterteilen könnten und eine Region mit Werten kleiner als 0, dann wählen Sie eine Zufallsstichprobe aus jeder Region aus.

Eindimensionales lateinisches Hypercube-Sampling

Die Idee hinter der eindimensionalen lateinischen Hypercube-Stichprobe ist einfach: Teilen Sie eine gegebene CDF in n verschiedene Regionen auf und wählen Sie in jeder Region zufällig einen Wert aus, um eine Stichprobe der Größe n zu erhalten.

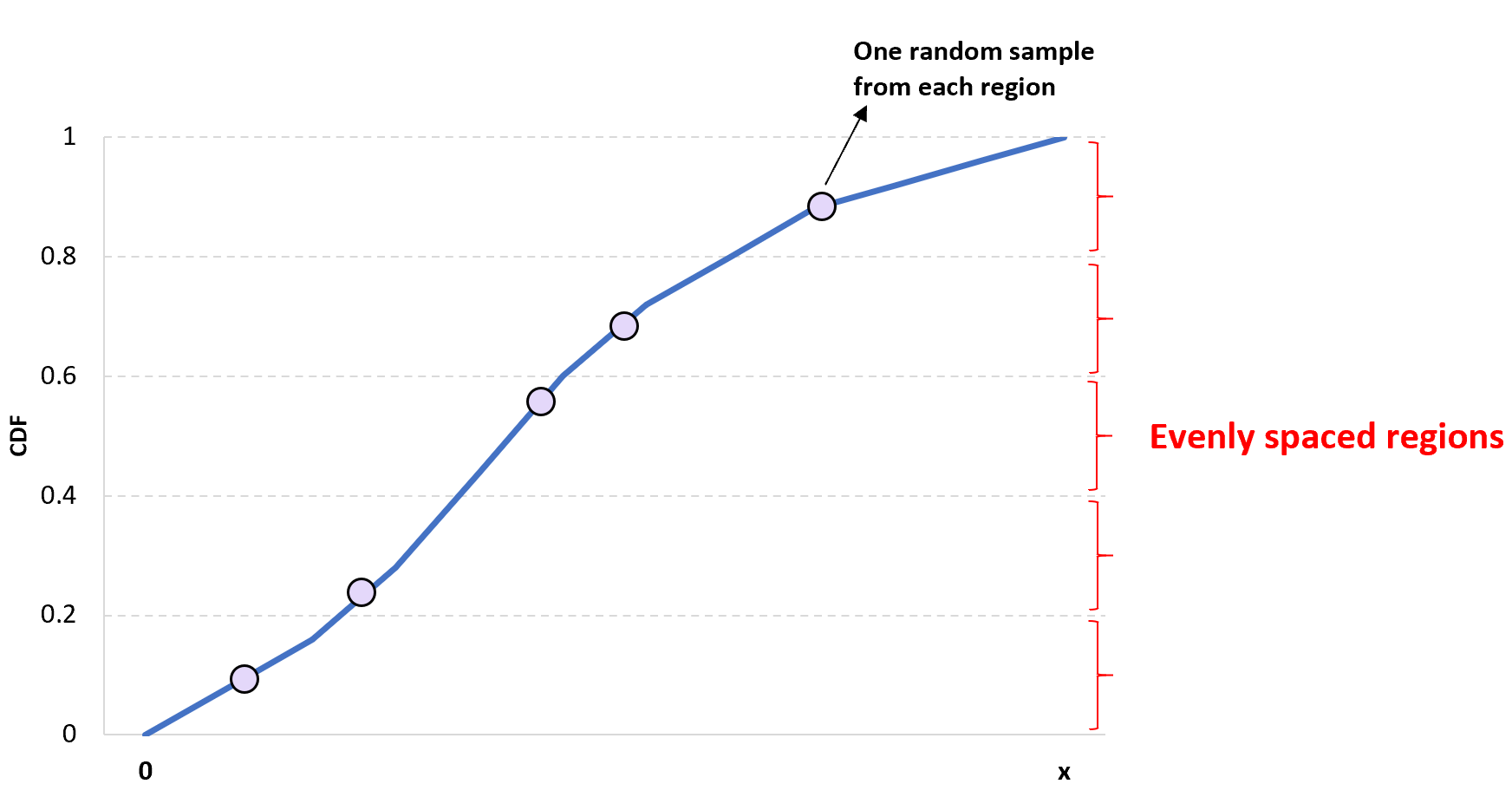
Der Vorteil dieses Ansatzes besteht darin, dass sichergestellt wird, dass mindestens ein Wert aus jeder Region in die Stichprobe einbezogen wird.

Abtastung zweidimensionaler lateinischer Hyperwürfel

Wir können die Idee der eindimensionalen lateinischen Hyperwürfel-Abtastung leicht auch auf zwei Dimensionen erweitern.

Für zwei Variablen, x und y, können wir den Stichprobenraum jeder Variablen in n gleichmäßig verteilte Bereiche unterteilen und aus jedem Stichprobenraum eine Zufallsstichprobe auswählen, um Zufallswerte in zwei Dimensionen zu erhalten.

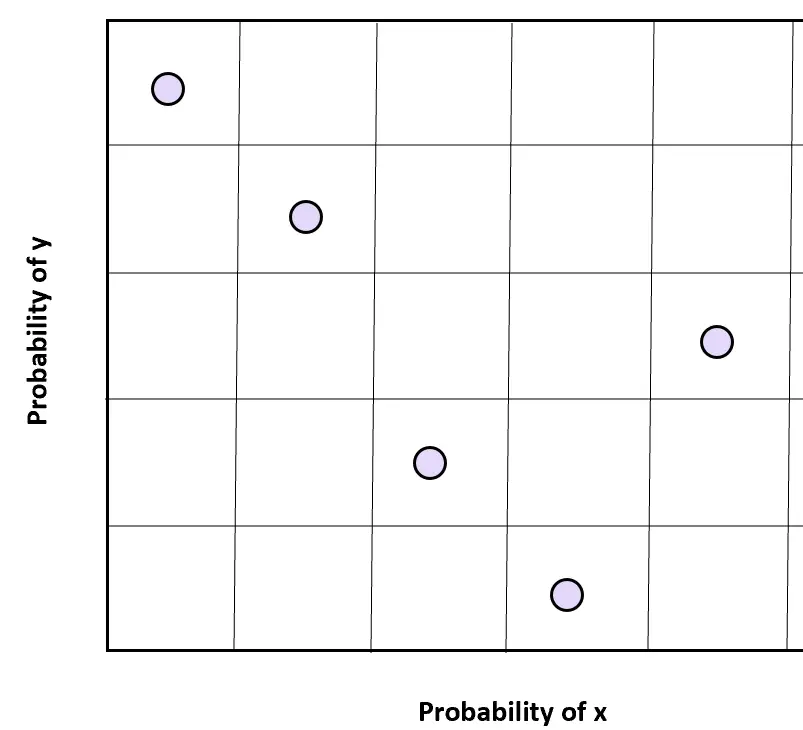
Es ist wichtig zu beachten, dass die beiden Variablen unabhängig sein müssen, damit diese Stichprobentechnik die gewünschten Ergebnisse erzielt.

N-dimensionales lateinisches Hypercube-Sampling

Um eine lateinische Hypercube-Probenahme in größeren Dimensionen durchzuführen, können wir einfach die Idee der zweidimensionalen lateinischen Hypercube-Probenahme auf noch mehr Dimensionen erweitern.

Jede Variable wird einfach in gleichmäßig verteilte Regionen unterteilt und dann werden aus jeder Region Zufallsstichproben ausgewählt, um eine kontrollierte Zufallsstichprobe zu erhalten.

Verwandte Themen: Was sind hochdimensionale Daten?

Warum Latin Hypercube-Sampling verwenden?

Der Hauptvorteil der lateinischen Hypercube-Stichprobe besteht darin, dass sie Stichproben erzeugt, die die tatsächliche zugrunde liegende Verteilung widerspiegeln und tendenziell viel kleinere Stichprobengrößen erfordern als einfache Zufallsstichproben .

Diese Stichprobenmethode kann besonders nützlich sein, wenn Sie mit Daten mit einer großen Anzahl von Dimensionen arbeiten und Zufallsstichproben benötigen, die sicher die tatsächliche zugrunde liegende Verteilung der Daten widerspiegeln.