Was ist ein lebensmitteltest? (erklärung & beispiel)

Ein Chow-Test ist ein vom Ökonomen Gregory Chow entwickelter statistischer Test, mit dem getestet wird, ob die Koeffizienten zweier verschiedener Regressionsmodelle für verschiedene Datensätze gleich sind.

Der Chow-Test wird typischerweise im Bereich der Ökonometrie mit Zeitreihendaten verwendet, um festzustellen, ob zu einem bestimmten Zeitpunkt ein Strukturbruch in den Daten vorliegt.

Betrachten Sie beispielsweise das folgende Streudiagramm:

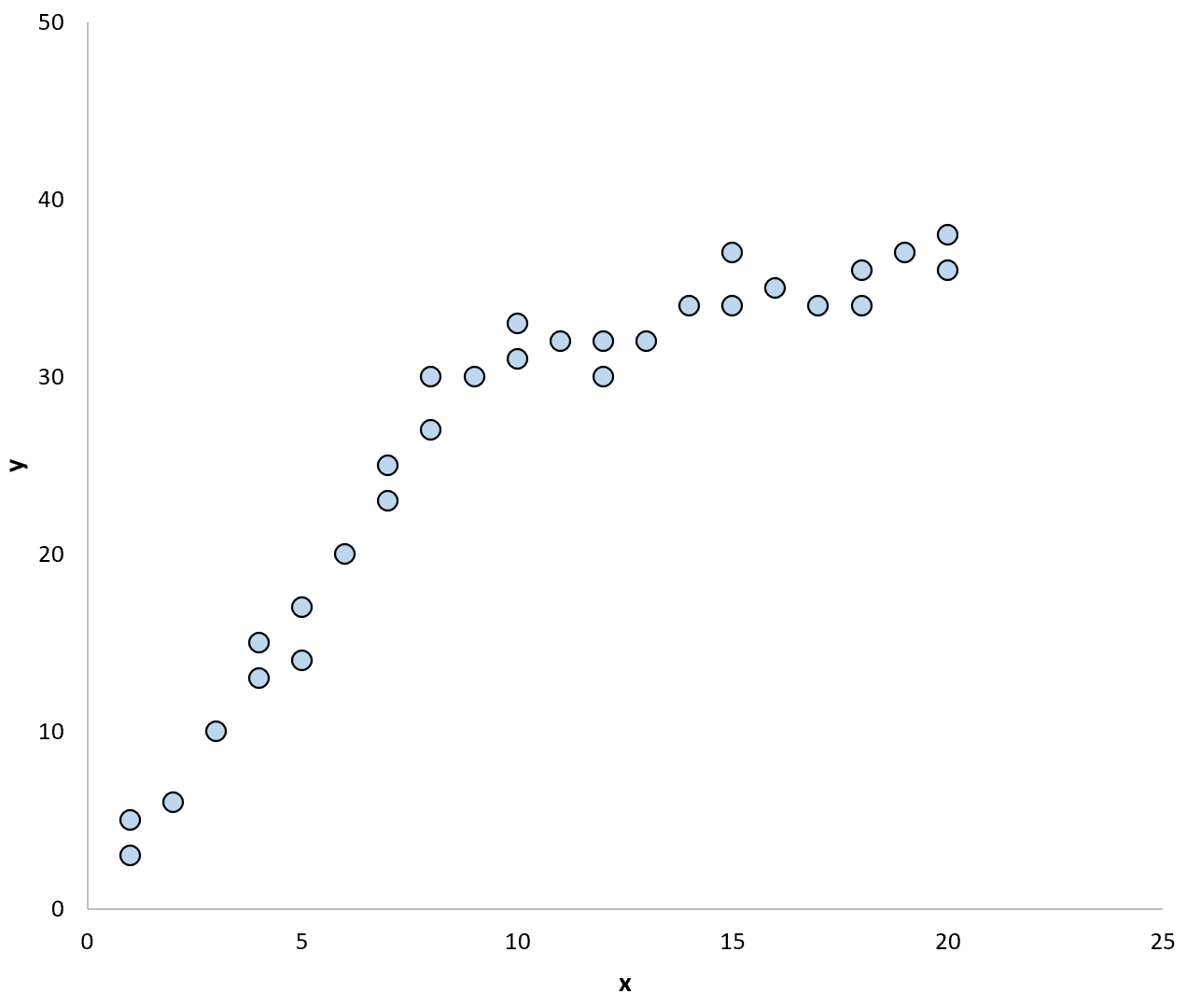
Wenn wir eine Regressionslinie verwenden würden, um das Modell in den Daten zusammenzufassen, könnte das so aussehen:

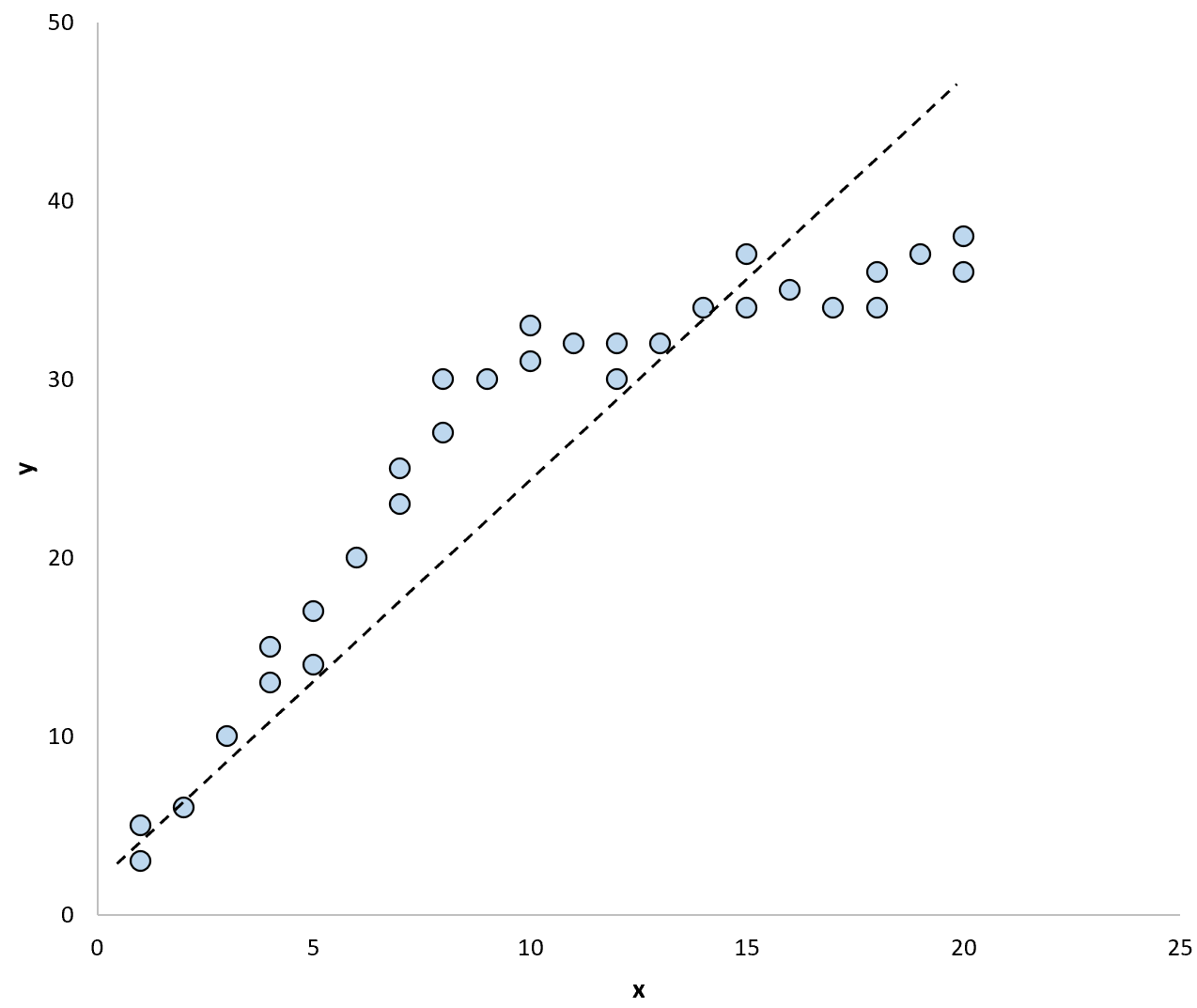
Und wenn wir zwei separate Regressionslinien verwenden würden, um das Modell in den Daten zusammenzufassen, könnte es so aussehen:

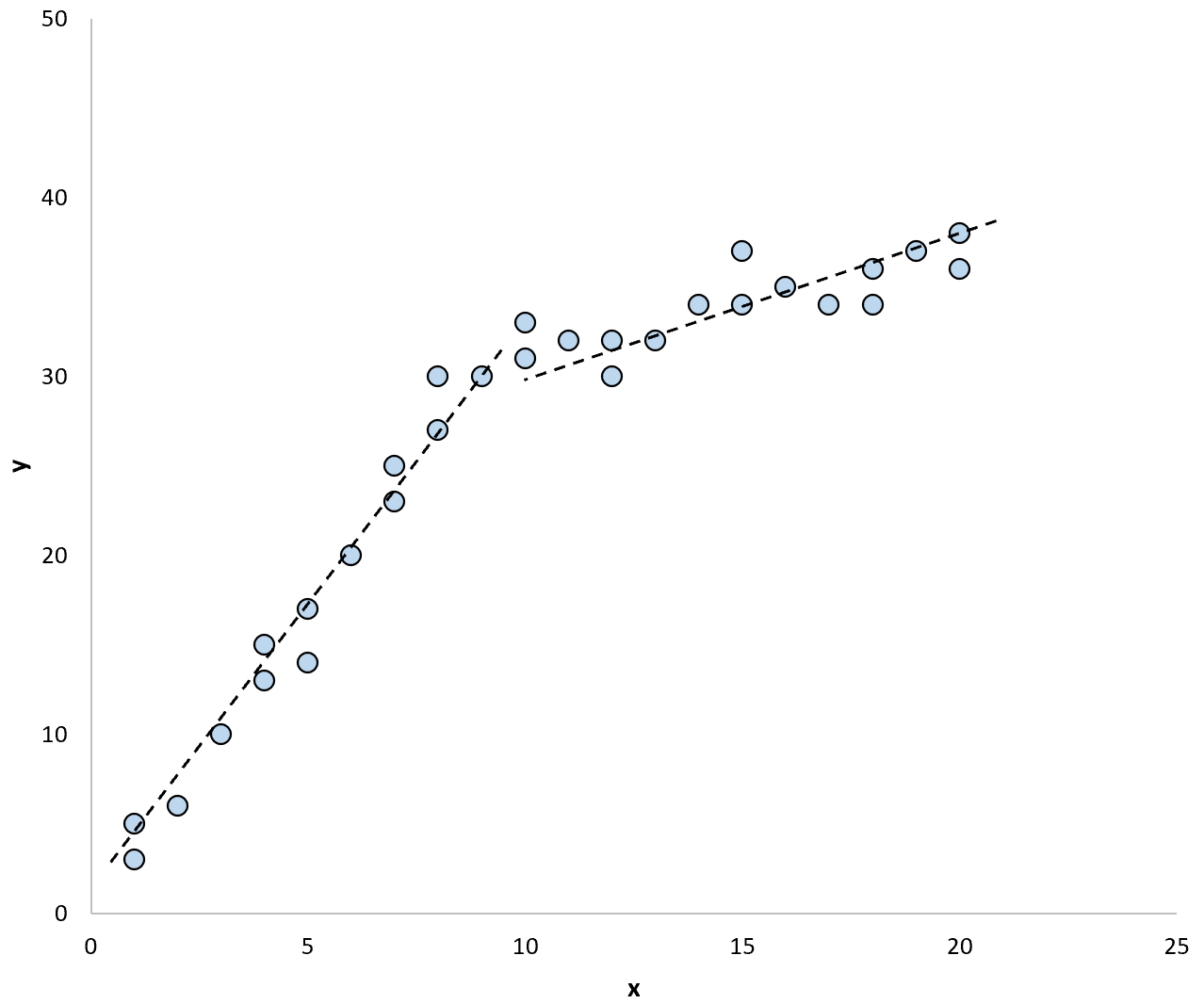
Mit dem Chow-Test können wir testen, ob die Regressionskoeffizienten jeder Regressionslinie gleich sind oder nicht.

Wenn der Test ergibt, dass die Koeffizienten zwischen den Regressionsgeraden nicht gleich sind, bedeutet dies, dass es signifikante Hinweise auf einen Strukturbruch in den Daten gibt. Mit anderen Worten: Der Datentrend ist vor und nach diesem strukturellen Bruchpunkt sehr unterschiedlich.

Wann ist der Chow-Test anzuwenden?

Die folgenden Beispiele veranschaulichen Situationen, in denen Sie möglicherweise einen Chow-Test durchführen möchten:

1. Bestimmen Sie, ob sich die Aktienkurse vor und nach einer Wahl unterschiedlich schnell bewegen.

2. Bestimmen Sie, ob sich die Immobilienpreise vor und nach einer Zinsänderung ändern.

3. Bestimmen Sie, ob der durchschnittliche Gewinn öffentlicher Unternehmen vor und nach der Verabschiedung eines neuen Steuergesetzes unterschiedlich ist.

In jeder Situation könnten wir einen Chow-Test verwenden, um zu bestimmen, ob es zu einem bestimmten Zeitpunkt einen strukturellen Bruchpunkt in den Daten gibt.

Schritte zur Durchführung eines Chow-Tests

Mit den folgenden Schritten können wir einen Chow-Test durchführen.

Schritt 1: Definieren Sie die Null- und Alternativhypothese.

Angenommen, wir passen das folgende Regressionsmodell an unseren gesamten Datensatz an:

• y _t = a + bx _1t + cx _t2 + ε

Nehmen wir als Nächstes an, wir unterteilen unsere Daten basierend auf einem strukturellen Haltepunkt in zwei Gruppen und passen die folgenden Regressionsmodelle an jede Gruppe an:

• y _t = a ₁ + b ₁ x _1t + c ₁ x _t2 + ε
• y _t = a ₂ + b ₂ x _1t + c ₂ x _t2 + ε

Für den Chow-Test würden wir die folgenden Null- und Alternativhypothesen verwenden:

• Null (H ₀ ): a ₁ = a ₂ , b ₁ = b ₂ und c ₁ = c ₂
• Alternative (H _A ): Mindestens einer der Vergleiche in Null ist nicht gleich.

Wenn wir die Nullhypothese ablehnen, haben wir genügend Beweise dafür, dass es einen strukturellen Bruchpunkt in den Daten gibt und dass zwei Regressionslinien besser zu den Daten passen können als eine.

Wenn wir die Nullhypothese nicht ablehnen, haben wir nicht genügend Beweise dafür, dass es einen strukturellen Bruchpunkt in den Daten gibt. In diesem Fall sagen wir, dass die Regressionslinien zu einer einzigen Regressionslinie zusammengefasst werden können, die das Muster der Daten gut genug darstellt.

Schritt 2: Berechnen Sie die Teststatistik.

Wenn wir die folgenden Begriffe definieren:

• S _T : Die Summe der Quadrate der Residuen der Gesamtdaten
• S ₁ , S ₂ : die Summe der Quadrate der Residuen jeder Gruppe
• N ₁ , N ₂ : Die Anzahl der Beobachtungen in jeder Gruppe
• k: Die Anzahl der Parameter

Wir können dann sagen, dass die Chow-Teststatistik ist:

Chow-Teststatistik = [(S _T – (S ₁ +S ₂ ))/k] / [(S ₁ +S ₂ )/ (N ₁ +N ₂ -2k)]

Diese Teststatistik folgt der F-Verteilung mit k und N ₁ + N ₂ -2k Freiheitsgraden.

Schritt 3: Lehnen Sie die Nullhypothese ab oder lehnen Sie sie nicht ab.

Wenn der mit dieser Teststatistik verbundene p-Wert unter einem bestimmten Signifikanzniveau liegt, können wir die Nullhypothese ablehnen und daraus schließen, dass es einen strukturellen Bruchpunkt in den Daten gibt.

Glücklicherweise ist die meiste Statistiksoftware in der Lage, einen Chow-Test durchzuführen, sodass Sie den Test wahrscheinlich nie manuell durchführen müssen.

Beispiel für die Durchführung eines Chow-Tests

In diesem Tutorial finden Sie ein schrittweises Beispiel für die Durchführung eines Chow-Tests für einen bestimmten Datensatz in R.

Notizen zum Chow-Test

Hier sind einige Hinweise, die Sie beim Chow-Test beachten sollten:

1. Der Test geht davon aus, dass die Residuen der Regressionsmodelle unabhängig und identisch von einer Normalverteilung mit unbekannter Varianz verteilt sind.

2. Der Chow-Test sollte nur verwendet werden, wenn der Strukturbruch, den Sie testen möchten, zu einem bekannten Zeitpunkt auftritt. Mit anderen Worten: Der Test sollte nicht wiederholt verwendet werden, um festzustellen, ob ein bestimmter Moment als Strukturbruch angesehen werden kann.