So führen sie den levene-test in spss durch

Der Levene-Test wird verwendet, um zu bestimmen, ob zwei oder mehr Gruppen gleiche Varianzen aufweisen.

Es wird häufig verwendet, da viele statistische Tests auf der Annahme beruhen, dass Gruppen gleiche Varianzen aufweisen.

In diesem Tutorial wird erklärt, wie Sie den Levene-Test in SPSS durchführen.

Beispiel: Levene-Test in SPSS

Forscher wollen wissen, ob drei verschiedene Düngemittel zu unterschiedlichem Pflanzenwachstum führen.

Sie wählen nach dem Zufallsprinzip 30 verschiedene Pflanzen aus und teilen sie in drei Gruppen zu je zehn Pflanzen auf, wobei sie jeder Gruppe einen anderen Dünger hinzufügen. Nach einem Monat messen sie die Höhe jeder Pflanze.

Der folgende Screenshot zeigt die Wachstumsmenge (in Zoll) für jede einzelne Pflanze sowie den Dünger (1, 2 oder 3), der auf die Pflanze aufgetragen wurde:

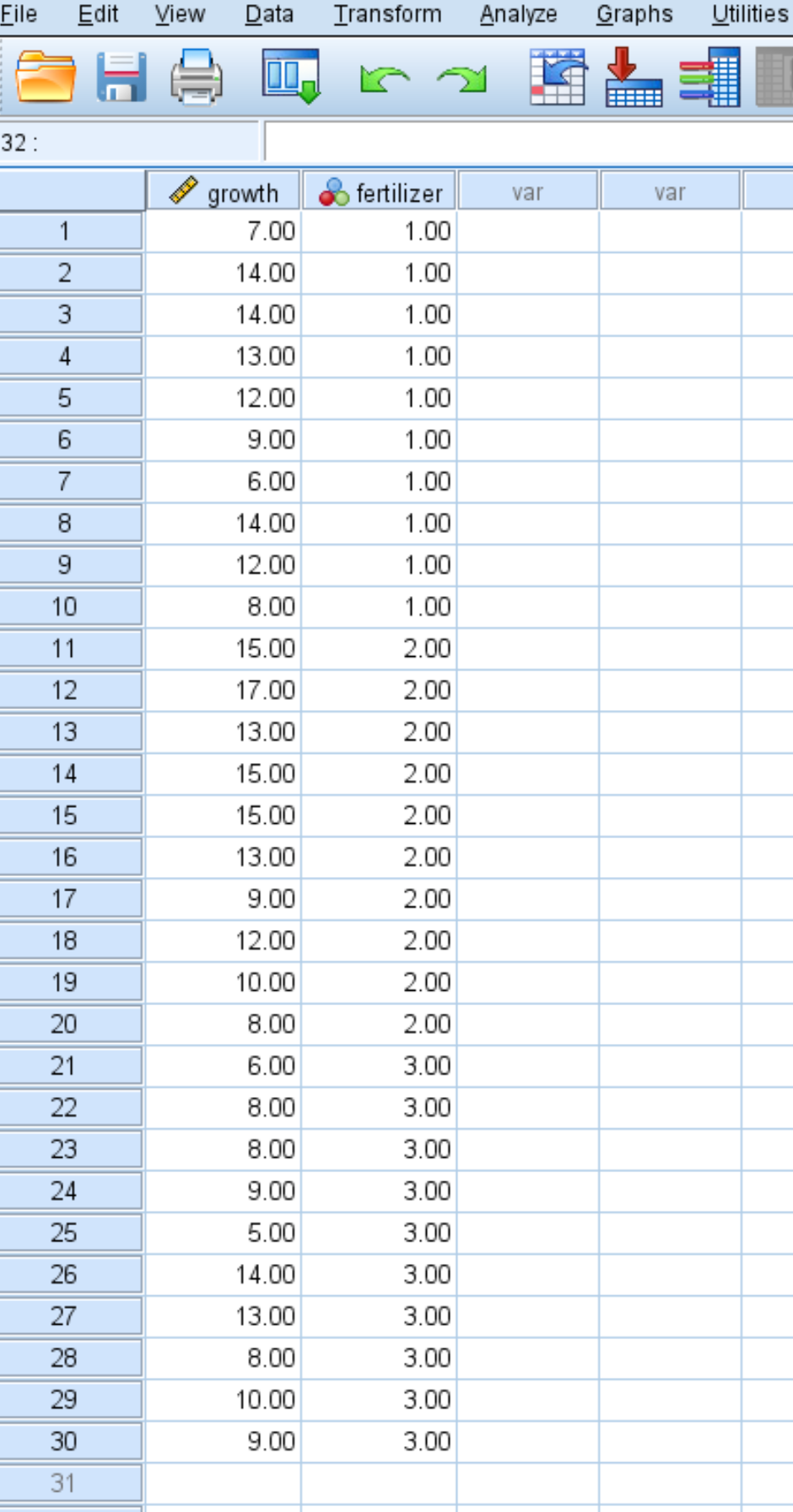
Führen Sie die folgenden Schritte aus, um den Levene-Test in SPSS durchzuführen und festzustellen, ob die drei Gruppen gleiche Varianzen aufweisen oder nicht.

Schritt 1: Wählen Sie die Option „Erkunden“.

Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Beschreibende Statistik“ und dann auf „Erkunden“ :

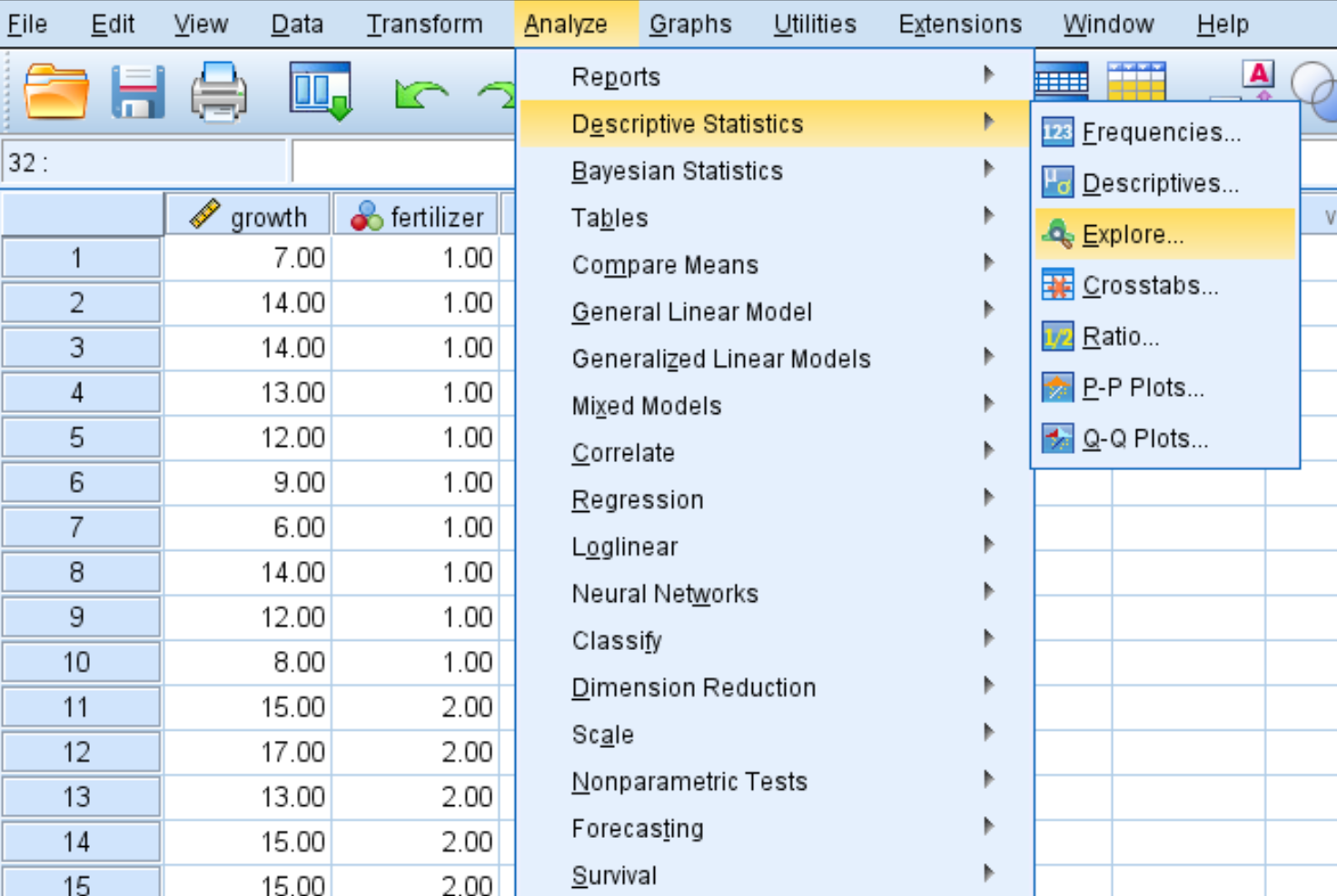
Schritt 2: Geben Sie die erforderlichen Werte ein, um den Test durchzuführen.

Ziehen Sie „Wachstum“ in das Feld unter „Abhängige Liste“ und ziehen Sie „Düngen“ .   in das Feld unter „Liste der Faktoren“ ein.

Klicken Sie dann auf Diagramme und stellen Sie sicher, dass die Leistungsschätzung ausgewählt ist. Klicken Sie dann auf Weiter . Klicken Sie dann auf OK .

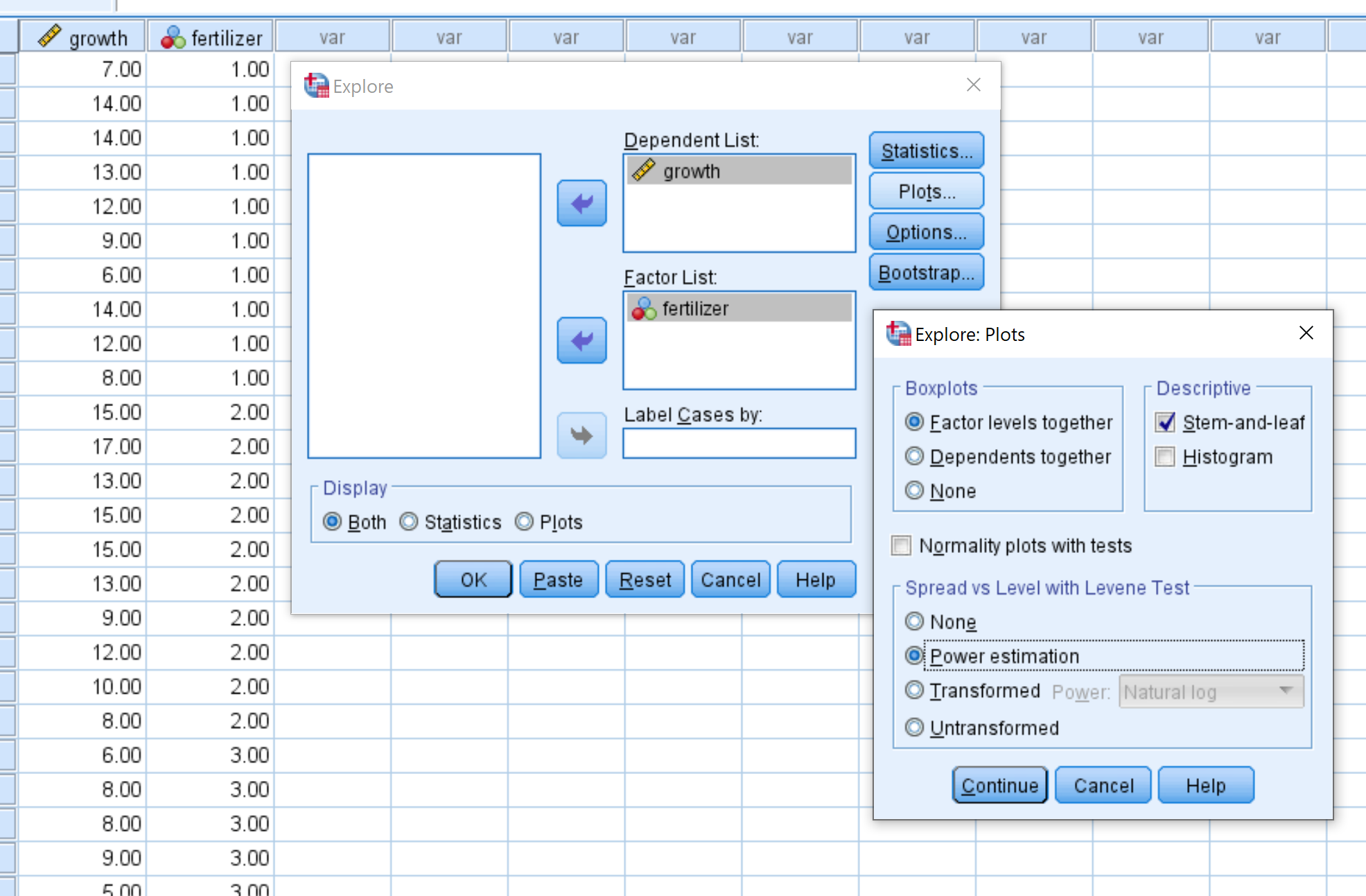
Schritt 3: Interpretieren Sie die Ergebnisse.

Sobald Sie auf OK klicken, werden die Levene-Testergebnisse angezeigt:

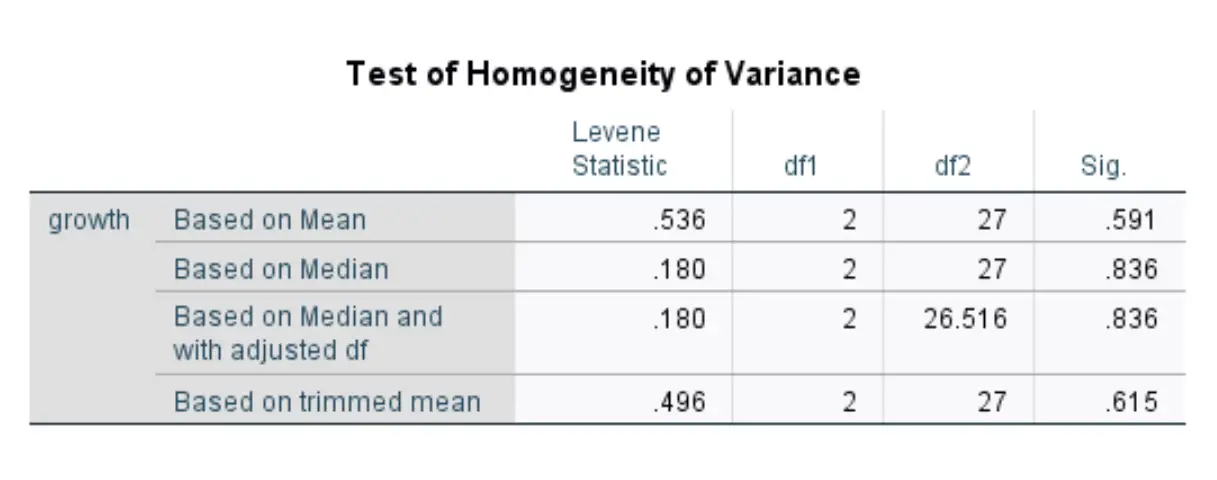
In dieser Tabelle werden Teststatistiken für vier verschiedene Versionen des Levene-Tests angezeigt. Die Zahlen, die uns interessieren, befinden sich in der ersten Zeile, in der die Ergebnisse des Levene-Tests basierend auf dem Mittelwert angezeigt werden.

Die Teststatistik beträgt 0,536 und der entsprechende p-Wert beträgt 0,591* .

Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Das bedeutet, dass uns keine ausreichenden Beweise dafür vorliegen, dass die Varianz im Pflanzenwachstum zwischen den drei Düngemitteln signifikant unterschiedlich ist.

Mit anderen Worten: Die drei Gruppen weisen gleiche Varianzen auf. Wenn wir einen statistischen Test (wie eine einfaktorielle ANOVA ) durchführen würden, der davon ausgeht, dass jede Gruppe die gleiche Varianz hat, dann wäre diese Annahme erfüllt.

* Dieser p-Wert entspricht einer F-Statistik von 0,536 mit Zähler df = 2 und Nenner df = 27. Dieser p-Wert kann auch mit dem F-Verteilungsrechner berechnet werden.