Lineare diskriminanzanalyse in r (schritt für schritt)
Die lineare Diskriminanzanalyse ist eine Methode, die Sie verwenden können, wenn Sie über eine Reihe von Prädiktorvariablen verfügen und eine Antwortvariable in zwei oder mehr Klassen klassifizieren möchten.
Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung einer linearen Diskriminanzanalyse in R.
Schritt 1: Laden Sie die erforderlichen Bibliotheken
Zuerst laden wir die notwendigen Bibliotheken für dieses Beispiel:
library (MASS)
library (ggplot2)
Schritt 2: Daten laden
Für dieses Beispiel verwenden wir den in R integrierten Iris- Datensatz. Der folgende Code zeigt, wie dieser Datensatz geladen und angezeigt wird:
#attach iris dataset to make it easy to work with attach(iris) #view structure of dataset str(iris) 'data.frame': 150 obs. of 5 variables: $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ... $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ... $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ... $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ... $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...
Wir können sehen, dass der Datensatz insgesamt 5 Variablen und 150 Beobachtungen enthält.
Für dieses Beispiel erstellen wir ein lineares Diskriminanzanalysemodell, um zu klassifizieren, zu welcher Art eine bestimmte Blume gehört.
Wir werden die folgenden Prädiktorvariablen im Modell verwenden:
- Kelchblattlänge
- Kelchblattbreite
- Blütenblattlänge
- Blütenblattbreite
Und wir werden sie verwenden, um die Antwortvariable „Species“ vorherzusagen, die die folgenden drei möglichen Klassen unterstützt:
- setosa
- versicolor
- Virginia
Schritt 3: Skalieren Sie die Daten
Eine der wichtigsten Annahmen der linearen Diskriminanzanalyse ist, dass jede der Prädiktorvariablen die gleiche Varianz aufweist. Eine einfache Möglichkeit, sicherzustellen, dass diese Annahme erfüllt ist, besteht darin, jede Variable so zu skalieren, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 aufweist.
Mit der Funktion „scale()“ können wir dies in R schnell erledigen:
#scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])
Wir können die Funktion apply() verwenden, um zu überprüfen, ob jede Prädiktorvariable jetzt einen Mittelwert von 0 und eine Standardabweichung von 1 hat:
#find mean of each predictor variable apply(iris[1:4], 2, mean) Sepal.Length Sepal.Width Petal.Length Petal.Width -4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 #find standard deviation of each predictor variable apply(iris[1:4], 2, sd) Sepal.Length Sepal.Width Petal.Length Petal.Width 1 1 1 1
Schritt 4: Erstellen Sie Trainings- und Testbeispiele
Als Nächstes teilen wir den Datensatz in einen Trainingssatz zum Trainieren des Modells und einen Testsatz zum Testen des Modells auf:
#make this example reproducible set.seed(1) #Use 70% of dataset as training set and remaining 30% as testing set sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3)) train <- iris[sample, ] test <- iris[!sample, ]
Schritt 5: Passen Sie das LDA-Modell an
Als nächstes verwenden wir die Funktion lda() aus dem MASS- Paket, um das LDA-Modell an unsere Daten anzupassen:
#fit LDA model model <- lda(Species~., data=train) #view model output model Call: lda(Species ~ ., data = train) Prior probabilities of groups: setosa versicolor virginica 0.3207547 0.3207547 0.3584906 Group means: Sepal.Length Sepal.Width Petal.Length Petal.Width setosa -1.0397484 0.8131654 -1.2891006 -1.2570316 versicolor 0.1820921 -0.6038909 0.3403524 0.2208153 virginica 0.9582674 -0.1919146 1.0389776 1.1229172 Coefficients of linear discriminants: LD1 LD2 Sepal.Length 0.7922820 0.5294210 Sepal.Width 0.5710586 0.7130743 Petal.Length -4.0762061 -2.7305131 Petal.Width -2.0602181 2.6326229 Proportion of traces: LD1 LD2 0.9921 0.0079
So interpretieren Sie die Modellergebnisse:
Gruppen-A-priori-Wahrscheinlichkeiten: Diese repräsentieren die Anteile jeder Art im Trainingssatz. Beispielsweise betrafen 35,8 % aller Beobachtungen im Trainingssatz die Art virginica .
Gruppendurchschnitte: Diese zeigen die Durchschnittswerte jeder Prädiktorvariablen für jede Art an.
Lineare Diskriminanzkoeffizienten: Diese zeigen die lineare Kombination von Prädiktorvariablen an, die zum Trainieren der Entscheidungsregel des LDA-Modells verwendet werden. Zum Beispiel:
- LD1: 0,792 * Kelchblattlänge + 0,571 * Kelchblattbreite – 4,076 * Blütenblattlänge – 2,06 * Blütenblattbreite
- LD2: 0,529 * Kelchblattlänge + 0,713 * Kelchblattbreite – 2,731 * Blütenblattlänge + 2,63 * Blütenblattbreite
Trace Proportion: Diese zeigen den Prozentsatz der Trennung an, der von jeder linearen Diskriminanzfunktion erreicht wird.
Schritt 6: Verwenden Sie das Modell, um Vorhersagen zu treffen
Sobald wir das Modell mithilfe unserer Trainingsdaten angepasst haben, können wir damit Vorhersagen zu unseren Testdaten treffen:
#use LDA model to make predictions on test data predicted <- predict (model, test) names(predicted) [1] "class" "posterior" "x"
Dies gibt eine Liste mit drei Variablen zurück:
- Klasse: die vorhergesagte Klasse
- Posterior: Die Posterior-Wahrscheinlichkeit , dass eine Beobachtung zu jeder Klasse gehört
- x: Lineare Diskriminanten
Wir können jedes dieser Ergebnisse für die ersten sechs Beobachtungen in unserem Testdatensatz schnell visualisieren:
#view predicted class for first six observations in test set head(predicted$class) [1] setosa setosa setosa setosa setosa setosa Levels: setosa versicolor virginica #view posterior probabilities for first six observations in test set head(predicted$posterior) setosa versicolor virginica 4 1 2.425563e-17 1.341984e-35 6 1 1.400976e-21 4.482684e-40 7 1 3.345770e-19 1.511748e-37 15 1 6.389105e-31 7.361660e-53 17 1 1.193282e-25 2.238696e-45 18 1 6.445594e-22 4.894053e-41 #view linear discriminants for first six observations in test set head(predicted$x) LD1 LD2 4 7.150360 -0.7177382 6 7.961538 1.4839408 7 7.504033 0.2731178 15 10.170378 1.9859027 17 8.885168 2.1026494 18 8.113443 0.7563902
Mit dem folgenden Code können wir sehen, für wie viel Prozent der Beobachtungen das LDA-Modell die Art korrekt vorhergesagt hat:
#find accuracy of model
mean(predicted$class==test$Species)
[1] 1
Es stellt sich heraus, dass das Modell die Art für 100 % der Beobachtungen in unserem Testdatensatz korrekt vorhergesagt hat.
In der realen Welt sagt ein LDA-Modell die Ergebnisse jeder Klasse selten richtig voraus, aber dieser Iris-Datensatz ist einfach so aufgebaut, dass Algorithmen für maschinelles Lernen tendenziell sehr gut funktionieren.
Schritt 7: Visualisieren Sie die Ergebnisse
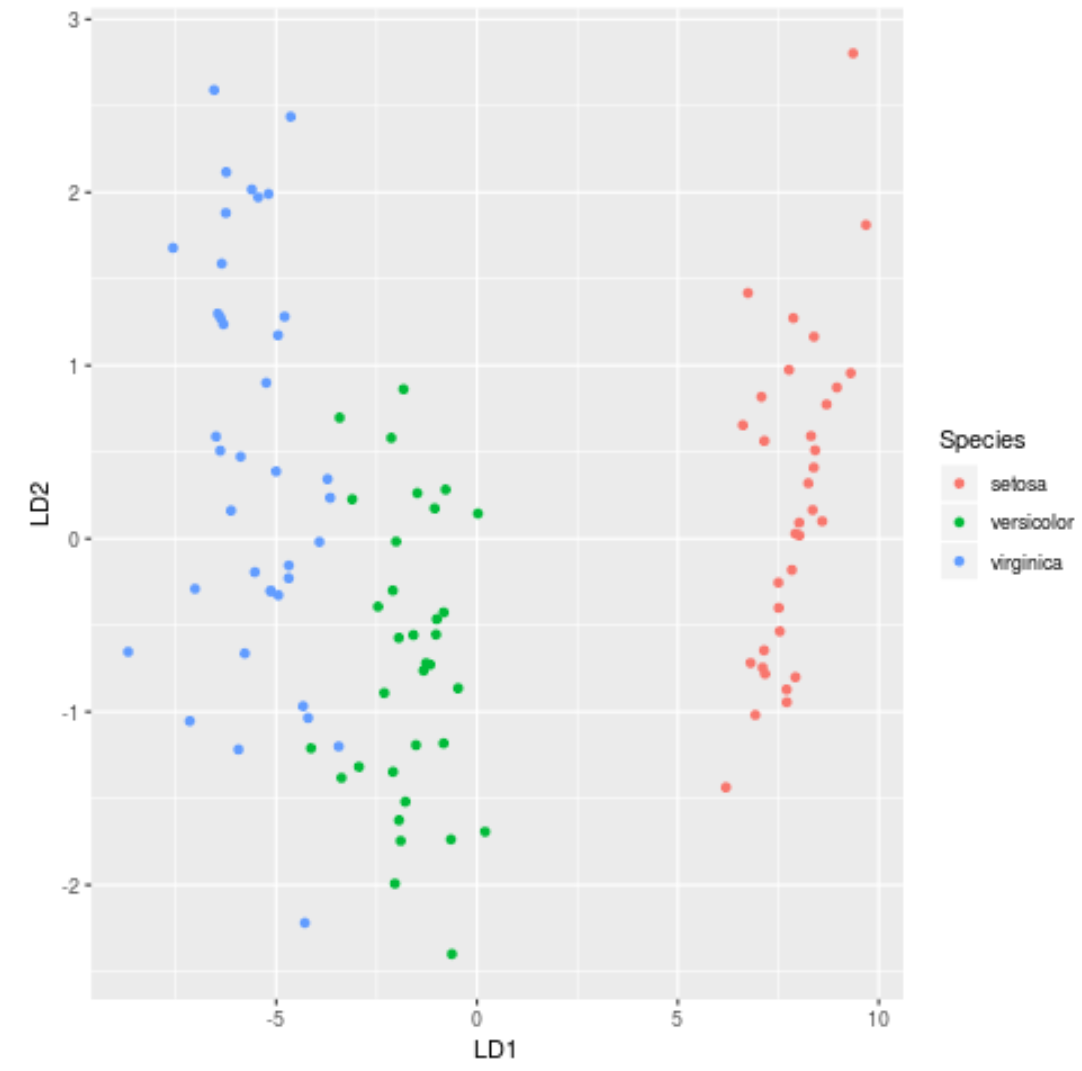
Schließlich können wir ein LDA-Diagramm erstellen, um die linearen Diskriminanten des Modells zu visualisieren und zu visualisieren, wie gut es die drei verschiedenen Arten in unserem Datensatz trennt:
#define data to plot lda_plot <- cbind(train, predict(model)$x) #createplot ggplot(lda_plot, aes (LD1, LD2)) + geom_point( aes (color=Species))
Den vollständigen R-Code, der in diesem Tutorial verwendet wird, finden Sie hier .