Einführung in die einfache lineare regression

Die einfache lineare Regression ist eine statistische Methode, mit der Sie die Beziehung zwischen zwei Variablen x und y verstehen können.

Eine Variable x wird als Prädiktorvariable bezeichnet.

Die andere Variable, y , wird als Antwortvariable bezeichnet.

Angenommen, wir haben den folgenden Datensatz mit dem Gewicht und der Größe von sieben Personen:

Das Gewicht sei die Prädiktorvariable und die Körpergröße die Antwortvariable.

Wenn wir diese beiden Variablen mithilfe eines Streudiagramms grafisch darstellen, mit Gewicht auf der x-Achse und Höhe auf der y-Achse, würde es wie folgt aussehen:

Angenommen, wir möchten den Zusammenhang zwischen Gewicht und Größe verstehen. Aus dem Streudiagramm können wir deutlich erkennen, dass mit zunehmendem Gewicht tendenziell auch die Körpergröße zunimmt. Um diese Beziehung zwischen Gewicht und Körpergröße jedoch tatsächlich zu quantifizieren , müssen wir eine lineare Regression verwenden.

Mithilfe der linearen Regression können wir die Linie finden, die am besten zu unseren Daten „passt“. Diese Linie ist als Regressionslinie der kleinsten Quadrate bekannt und kann verwendet werden, um uns zu helfen, die Beziehungen zwischen Gewicht und Größe zu verstehen.

Normalerweise verwenden Sie Software wie Microsoft Excel, SPSS oder einen Grafikrechner, um die Gleichung für diese Linie zu finden.

Die Formel für die beste Anpassungsgerade lautet:

ŷ = b ₀ + b ₁ x

Dabei ist ŷ der vorhergesagte Wert der Antwortvariablen, b ₀ der Achsenabschnitt, b ₁ der Regressionskoeffizient und x der Wert der Prädiktorvariablen.

Verwandte Themen: 4 Beispiele für die Verwendung der linearen Regression im wirklichen Leben

Finden Sie die „am besten geeignete Linie“

Für dieses Beispiel können wir unsere Daten einfach in den statistischen linearen Regressionsrechner eingeben und auf Berechnen klicken:

Der Rechner findet automatisch die Regressionsgerade der kleinsten Quadrate :

ŷ = 32,7830 + 0,2001x

Wenn wir aus unserem vorherigen Streudiagramm herauszoomen und diese Linie zum Diagramm hinzufügen, würde es so aussehen:

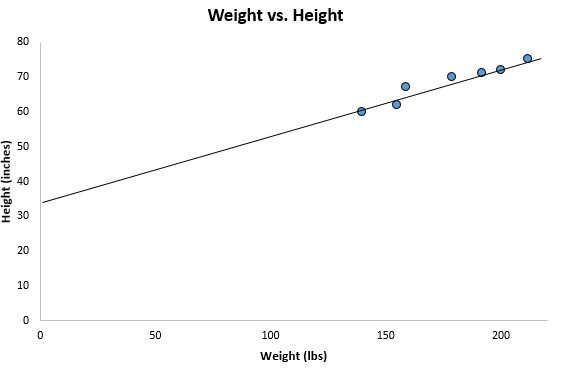
Beachten Sie, dass unsere Datenpunkte eng um diese Linie verstreut sind. Tatsächlich ist diese Regressionslinie der kleinsten Quadrate unter allen möglichen Linien, die wir zeichnen könnten, die Linie, die am besten zu unseren Daten passt.

So interpretieren Sie eine Regressionslinie der kleinsten Quadrate

So interpretieren Sie diese Regressionslinie der kleinsten Quadrate: ŷ = 32,7830 + 0,2001x

_b0 = 32,7830 . Das bedeutet, dass die vorhergesagte Körpergröße 32,7830 Zoll beträgt, wenn das Gewicht der Prädiktorvariablen null Pfund beträgt. Manchmal kann es nützlich sein, den Wert von b ₀ zu kennen, aber in diesem speziellen Beispiel macht es keinen Sinn, b ₀ zu interpretieren, da eine Person nicht null Pfund wiegen kann.

_b1 = 0,2001 . Dies bedeutet, dass ein Anstieg von x um eine Einheit mit einem Anstieg von y um 0,2001 Einheiten verbunden ist. In diesem Fall ist eine Gewichtszunahme von einem Pfund mit einer Zunahme der Körpergröße um 0,2001 Zoll verbunden.

So verwenden Sie die Regressionslinie der kleinsten Quadrate

Mit dieser Regressionslinie der kleinsten Quadrate können wir Fragen beantworten wie:

Wie groß sollte jemand sein, der 170 Pfund wiegt?

Um diese Frage zu beantworten, können wir einfach 170 in unsere Regressionsgerade für x einfügen und nach y auflösen:

ŷ = 32,7830 + 0,2001(170) = 66,8 Zoll

Wie groß sollten wir bei jemandem mit einem Gewicht von 150 Pfund rechnen?

Um diese Frage zu beantworten, können wir 150 in unsere Regressionsgerade für x einfügen und nach y auflösen:

ŷ = 32,7830 + 0,2001(150) = 62,798 Zoll

Achtung: Wenn Sie zur Beantwortung solcher Fragen eine Regressionsgleichung verwenden, achten Sie darauf, nur Werte für die Prädiktorvariable zu verwenden, die innerhalb des Bereichs der Prädiktorvariablen im Datensatz liegen. Ursprung, den wir zum Generieren der Regressionslinie der kleinsten Quadrate verwendet haben. Beispielsweise lagen die Gewichte in unserem Datensatz zwischen 140 und 212 Pfund. Daher ist es sinnvoll, Fragen zur erwarteten Körpergröße zu beantworten, wenn das Gewicht zwischen 140 und 212 Pfund liegt.

Das Bestimmtheitsmaß

Eine Möglichkeit zu messen, wie gut die Regressionslinie der kleinsten Quadrate zu den Daten „passt“, ist die Verwendung des Bestimmtheitsmaßes , das mit R ² bezeichnet wird.

Das Bestimmtheitsmaß ist der Anteil der Varianz der Antwortvariablen, der durch die Prädiktorvariable erklärt werden kann.

Das Bestimmtheitsmaß kann zwischen 0 und 1 variieren. Ein Wert von 0 gibt an, dass die Antwortvariable überhaupt nicht durch die Prädiktorvariable erklärt werden kann. Ein Wert von 1 gibt an, dass die Antwortvariable perfekt und fehlerfrei durch die Prädiktorvariable erklärt werden kann.

Ein R ² zwischen 0 und 1 gibt an, inwieweit die Antwortvariable durch die Prädiktorvariable erklärt werden kann. Beispielsweise bedeutet ein R ² von 0,2, dass 20 % der Varianz der Antwortvariablen durch die Prädiktorvariable erklärt werden können; Ein R ² von 0,77 bedeutet, dass 77 % der Varianz der Antwortvariablen durch die Prädiktorvariable erklärt werden können.

Beachten Sie, dass wir in unserem vorherigen Ergebnis ein R ² von 0,9311 erhalten haben, was darauf hinweist, dass 93,11 % der Höhenvariabilität durch die Gewichtungsprädiktorvariable erklärt werden können:

Dies zeigt uns, dass das Gewicht ein sehr guter Indikator für die Körpergröße ist.

Annahmen zur linearen Regression

Damit die Ergebnisse eines linearen Regressionsmodells gültig und zuverlässig sind, müssen wir überprüfen, ob die folgenden vier Annahmen erfüllt sind:

1. Lineare Beziehung: Es besteht eine lineare Beziehung zwischen der unabhängigen Variablen x und der abhängigen Variablen y.

2. Unabhängigkeit: Die Residuen sind unabhängig. Insbesondere besteht keine Korrelation zwischen aufeinanderfolgenden Residuen in Zeitreihendaten.

3. Homoskedastizität: Die Residuen haben auf jeder Ebene von x eine konstante Varianz.

4. Normalität: Die Modellresiduen sind normalverteilt.

Wenn eine oder mehrere dieser Annahmen nicht erfüllt sind, können die Ergebnisse unserer linearen Regression unzuverlässig oder sogar irreführend sein.

In diesem Artikel finden Sie eine Erläuterung der einzelnen Annahmen, wie Sie feststellen können, ob die Annahme erfüllt ist, und was zu tun ist, wenn die Annahme nicht erfüllt ist.