So führen sie eine lineare regression in google sheets durch
Die lineare Regression ist eine Methode, mit der die Beziehung zwischen einer oder mehreren erklärenden Variablen und einer Antwortvariablen quantifiziert werden kann.
Wir verwenden die einfache lineare Regression, wenn es nur eine erklärende Variable gibt, und die multiple lineare Regression, wenn es zwei oder mehr erklärende Variablen gibt.
Beide Arten von Regressionen können mit der Google Sheets-Funktion LINEST() durchgeführt werden, die die folgende Syntax verwendet:
LINEST (bekannte_Daten_y, bekannte_Daten_x, berechne_b, ausführlich)
Gold:
- known_data_y: Array von Antwortwerten
- known_data_x: Tabelle mit erklärenden Werten
- berechne_b: gibt an, ob der Achsenabschnitt berechnet werden soll oder nicht. Dies ist standardmäßig WAHR und wir belassen dies auch für die lineare Regression.
- ausführlich: Gibt an, ob zusätzliche Regressionsstatistiken bereitgestellt werden sollen, die über die Steigung und den Achsenabschnitt hinausgehen. Dies ist standardmäßig FALSE, aber wir werden in unseren Beispielen angeben, dass es TRUE ist.
Die folgenden Beispiele zeigen, wie Sie diese Funktion in der Praxis nutzen können.
Einfache lineare Regression in Google Sheets
Angenommen, wir möchten den Zusammenhang zwischen Lernstunden und Prüfungsergebnissen verstehen. Prüfungsvorbereitung und die bei der Prüfung erzielte Note.
Um diesen Zusammenhang zu untersuchen, können wir eine einfache lineare Regression durchführen, indem wir die untersuchten Stunden als erklärende Variable und die Prüfungsergebnisse als Antwortvariable verwenden.
Der folgende Screenshot zeigt, wie eine einfache lineare Regression anhand eines Datensatzes von 20 Schülern mit der folgenden Formel in Zelle D2 durchgeführt wird:
= LINIE ( B2:B21 , A2:A21 , TRUE , TRUE )
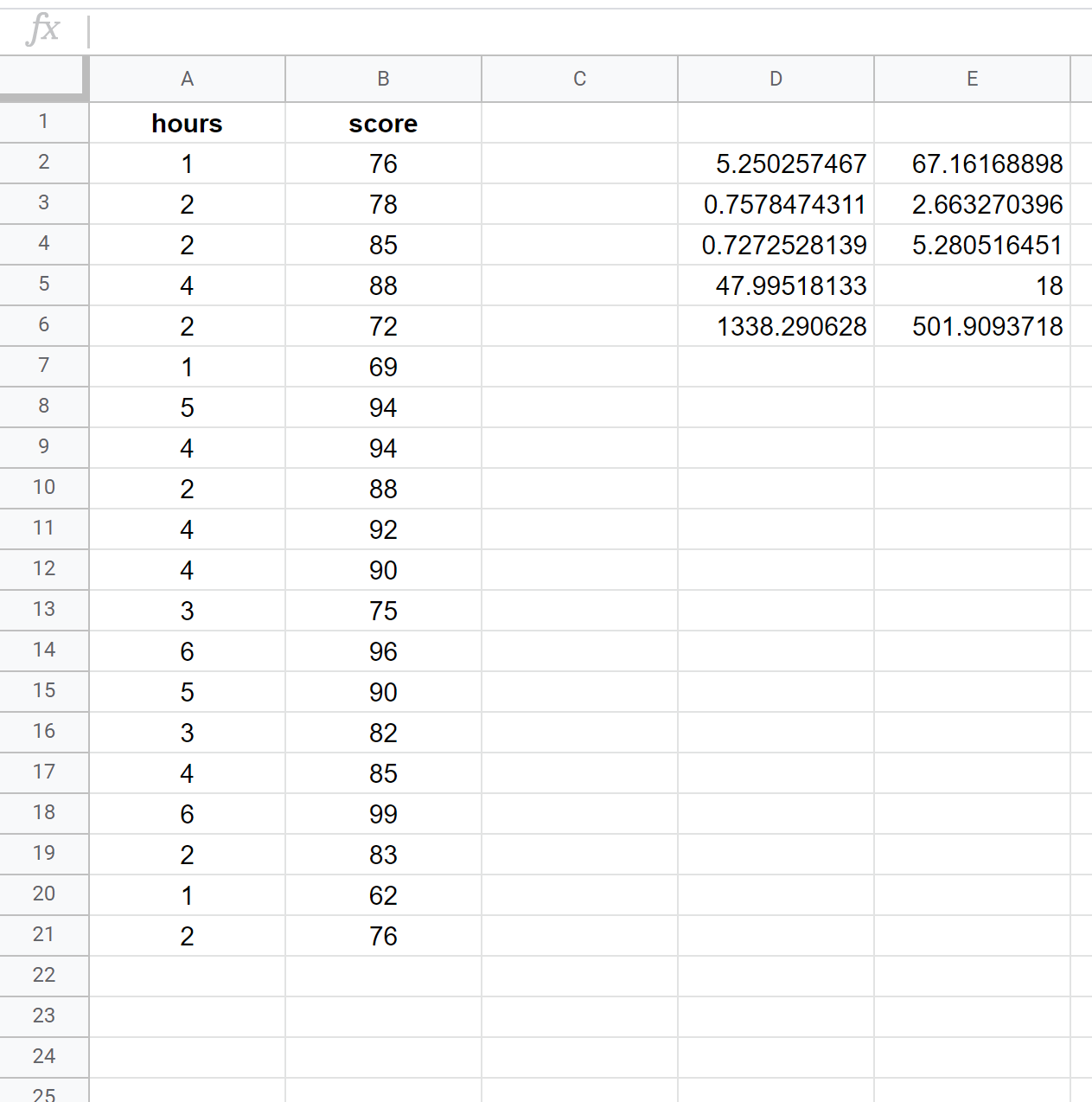
Der folgende Screenshot enthält Anmerkungen zur Ausgabe:
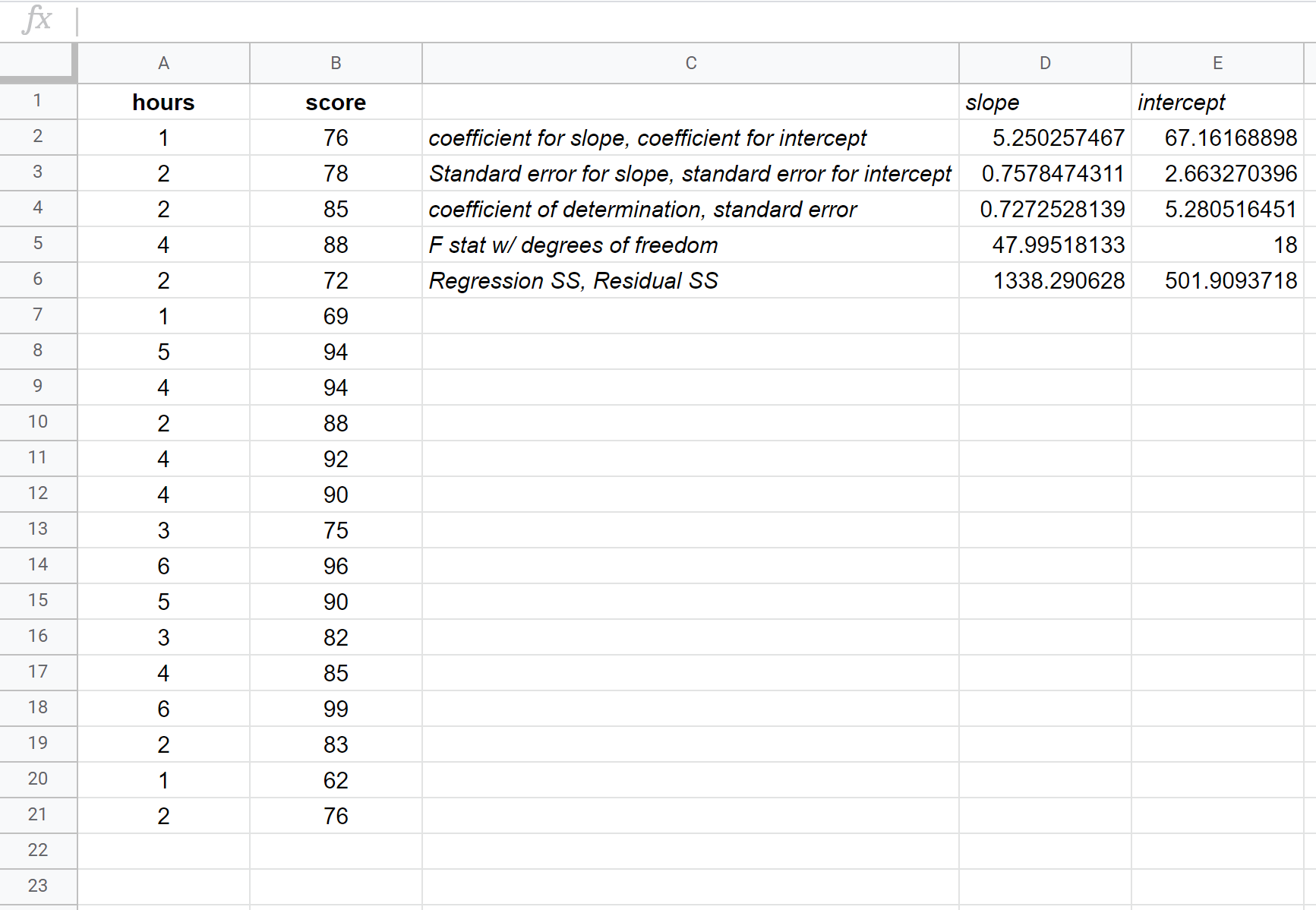
So interpretieren Sie die relevantesten Zahlen im Ergebnis:
R-Quadrat: 0,72725 . Dies wird als Bestimmtheitsmaß bezeichnet. Es ist der Anteil der Varianz der Antwortvariablen, der durch die erklärende Variable erklärt werden kann. In diesem Beispiel können etwa 72,73 % der Abweichungen bei den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden.
Standardfehler: 5,2805 . Dies ist der durchschnittliche Abstand zwischen den beobachteten Werten und der Regressionsgeraden. In diesem Beispiel weichen die beobachteten Werte im Durchschnitt um 5,2805 Einheiten von der Regressionsgeraden ab.
Koeffizienten: Die Koeffizienten liefern uns die Zahlen, die wir zum Schreiben der geschätzten Regressionsgleichung benötigen. In diesem Beispiel lautet die geschätzte Regressionsgleichung:
Prüfungsergebnis = 67,16 + 5,2503*(Stunden)
Wir interpretieren den Stundenkoeffizienten so, dass sich die Prüfungspunktzahl für jede weitere gelernte Stunde im Durchschnitt um 5,2503 erhöhen sollte. Wir interpretieren den Koeffizienten des Achsenabschnitts so, dass die erwartete Prüfungspunktzahl für einen Studenten, der null Stunden studiert, 67,16 beträgt.
Mit dieser geschätzten Regressionsgleichung können wir die erwartete Prüfungspunktzahl eines Studenten basierend auf der Anzahl der Lernstunden berechnen. Beispielsweise sollte ein Student, der drei Stunden lang lernt, eine Prüfungspunktzahl von 82,91 erreichen:
Prüfungsergebnis = 67,16 + 5,2503*(3) = 82,91
Multiple lineare Regression in Google Sheets
Angenommen, wir möchten wissen, ob die Anzahl der Lernstunden und die Anzahl der abgelegten Vorbereitungsprüfungen die Note beeinflussen, die ein Student bei einer bestimmten Hochschulaufnahmeprüfung erhält.
Um diesen Zusammenhang zu untersuchen, können wir eine multiple lineare Regression durchführen, indem wir die untersuchten Stunden und vorbereitenden Prüfungen als erklärende Variablen und die Prüfungsergebnisse als Antwortvariable verwenden.
Der folgende Screenshot zeigt, wie man eine multiple lineare Regression anhand eines Datensatzes von 20 Schülern mit der folgenden Formel in Zelle E2 durchführt:
= RECHTS ( C2:C21 , A2:B21 , WAHR , WAHR )
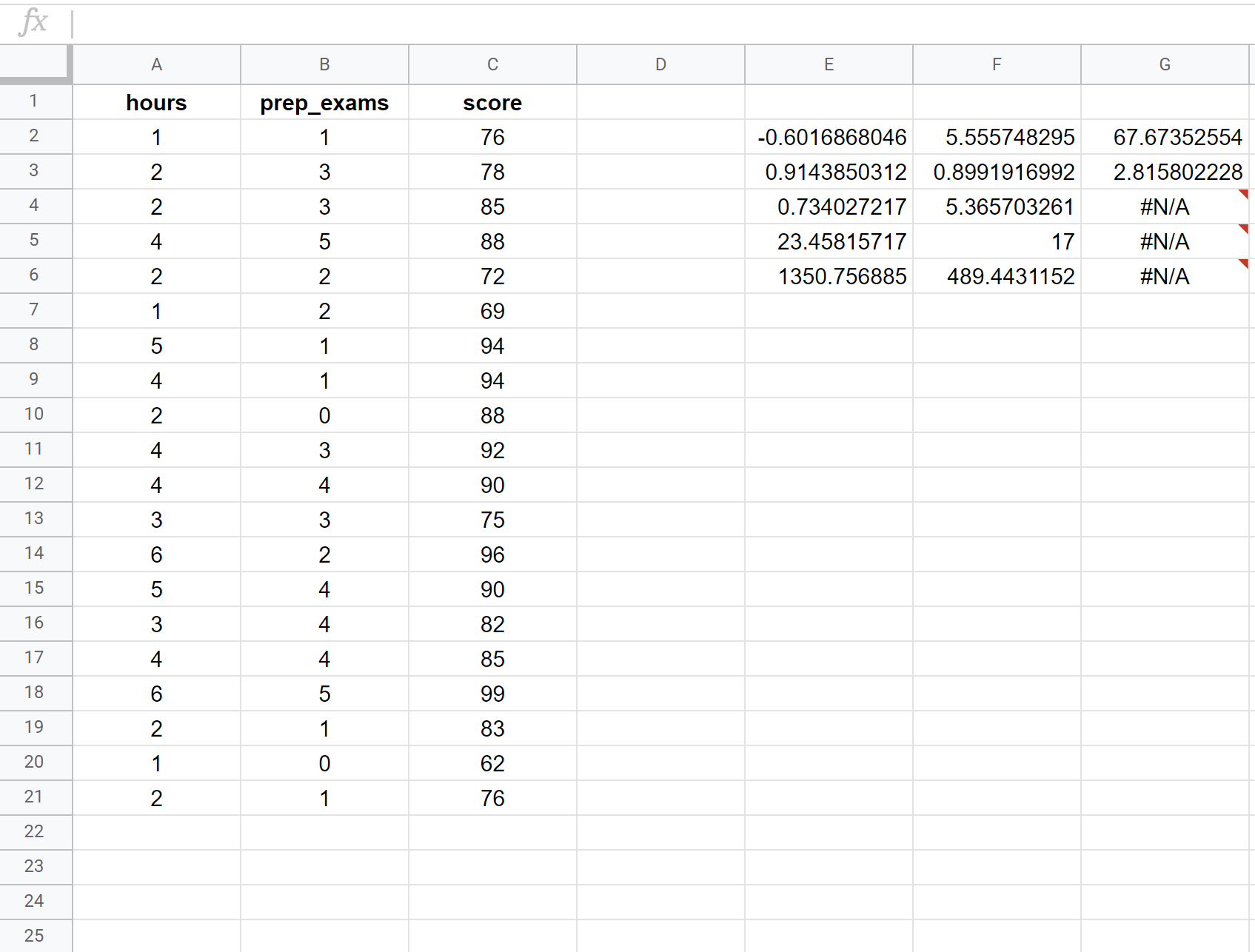
So interpretieren Sie die relevantesten Zahlen im Ergebnis:
R-Quadrat: 0,734 . Dies wird als Bestimmtheitsmaß bezeichnet. Es ist der Anteil der Varianz der Antwortvariablen, der durch die erklärenden Variablen erklärt werden kann. In diesem Beispiel lassen sich 73,4 % der Abweichungen bei den Prüfungsergebnissen durch die Anzahl der gelernten Stunden und die Anzahl der abgelegten Vorbereitungsprüfungen erklären.
Standardfehler: 5,3657 . Dies ist der durchschnittliche Abstand zwischen den beobachteten Werten und der Regressionsgeraden. In diesem Beispiel weichen die beobachteten Werte im Durchschnitt um 5,3657 Einheiten von der Regressionsgeraden ab.
Geschätzte Regressionsgleichung: Wir können die Koeffizienten aus der Modellausgabe verwenden, um die folgende geschätzte Regressionsgleichung zu erstellen:
Prüfungsergebnis = 67,67 + 5,56*(Stunden) – 0,60*(Vorbereitungsprüfungen)
Wir können diese geschätzte Regressionsgleichung verwenden, um die erwartete Prüfungspunktzahl für einen Studenten zu berechnen, basierend auf der Anzahl der Lernstunden und der Anzahl der von ihm abgelegten Übungsprüfungen. Ein Student, der beispielsweise drei Stunden lernt und eine Vorbereitungsprüfung ablegt, sollte eine Note von 83,75 erhalten:
Prüfungsergebnis = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Zusätzliche Ressourcen
In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in Google Sheets ausführen:
So führen Sie eine Polynomregression in Google Sheets durch
So erstellen Sie ein Restdiagramm in Google Sheets