Die vier annahmen der linearen regression

Die lineare Regression ist eine nützliche statistische Methode, mit der wir die Beziehung zwischen zwei Variablen x und y verstehen können. Bevor wir jedoch eine lineare Regression durchführen, müssen wir zunächst sicherstellen, dass vier Annahmen erfüllt sind:

1. Lineare Beziehung: Es besteht eine lineare Beziehung zwischen der unabhängigen Variablen x und der abhängigen Variablen y.

2. Unabhängigkeit: Die Residuen sind unabhängig. Insbesondere besteht keine Korrelation zwischen aufeinanderfolgenden Residuen in Zeitreihendaten.

3. Homoskedastizität: Die Residuen haben auf jeder Ebene von x eine konstante Varianz.

4. Normalität: Die Modellresiduen sind normalverteilt.

Wenn eine oder mehrere dieser Annahmen nicht erfüllt sind, können die Ergebnisse unserer linearen Regression unzuverlässig oder sogar irreführend sein.

In diesem Artikel geben wir eine Erklärung für jede Annahme, wie Sie feststellen können, ob die Annahme erfüllt ist, und was zu tun ist, wenn die Annahme nicht erfüllt ist.

Hypothese 1: Lineare Beziehung

Erläuterung

Die erste Annahme der linearen Regression ist, dass zwischen der unabhängigen Variablen x und der unabhängigen Variablen y eine lineare Beziehung besteht.

So ermitteln Sie, ob diese Annahme erfüllt ist

Der einfachste Weg, um festzustellen, ob diese Annahme erfüllt ist, besteht darin, ein Streudiagramm von x über y zu erstellen. Dadurch können Sie visuell erkennen, ob zwischen den beiden Variablen ein linearer Zusammenhang besteht. Wenn es den Anschein hat, dass die Punkte im Diagramm entlang einer geraden Linie liegen könnten, dann besteht eine Art lineare Beziehung zwischen den beiden Variablen und diese Annahme ist erfüllt.

Beispielsweise scheinen die Punkte in der folgenden Grafik auf einer geraden Linie zu liegen, was darauf hindeutet, dass zwischen x und y eine lineare Beziehung besteht:

In der folgenden Grafik scheint es jedoch keine lineare Beziehung zwischen x und y zu geben:

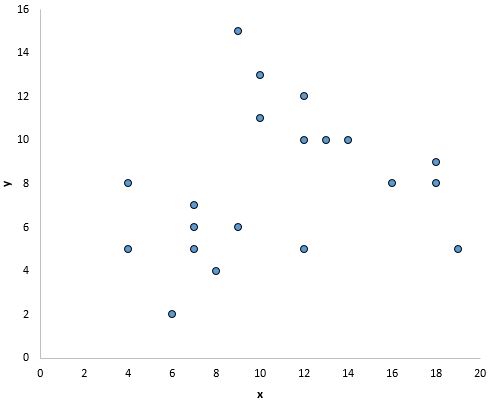
Und in dieser Grafik scheint es eine klare Beziehung zwischen x und y zu geben, aber keine lineare Beziehung :

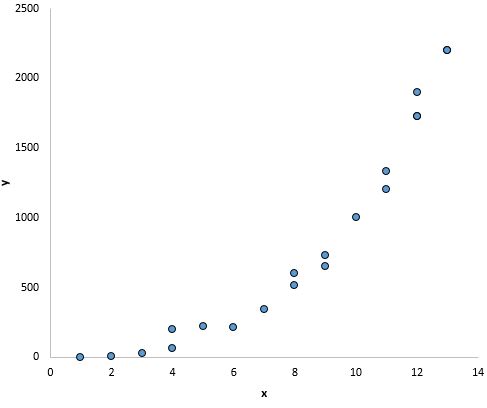
Was tun, wenn diese Annahme nicht respektiert wird?

Wenn Sie ein Streudiagramm der Werte für x und y erstellen und feststellen, dass zwischen den beiden Variablen keine lineare Beziehung besteht, haben Sie mehrere Möglichkeiten:

1. Wenden Sie eine nichtlineare Transformation auf die unabhängige und/oder abhängige Variable an. Gängige Beispiele sind die Berechnung des Logarithmus, der Quadratwurzel oder des Kehrwerts der unabhängigen und/oder abhängigen Variablen.

2. Fügen Sie dem Modell eine weitere unabhängige Variable hinzu. Wenn beispielsweise das Diagramm von x vs. y eine parabolische Form hat, kann es sinnvoll sein, X ² als zusätzliche unabhängige Variable in das Modell aufzunehmen.

Hypothese 2: Unabhängigkeit

Erläuterung

Die nächste Annahme der linearen Regression ist, dass die Residuen unabhängig sind. Dies ist besonders relevant, wenn mit Zeitreihendaten gearbeitet wird. Im Idealfall möchten wir nicht, dass es einen Trend zwischen aufeinanderfolgenden Residuen gibt. Beispielsweise sollten die Rückstände im Laufe der Zeit nicht kontinuierlich zunehmen.

So ermitteln Sie, ob diese Annahme erfüllt ist

Der einfachste Weg, um zu testen, ob diese Annahme zutrifft, besteht darin, sich ein Zeitreihendiagramm der Residuen anzusehen, bei dem es sich um ein Diagramm der Residuen gegenüber der Zeit handelt. Im Idealfall sollten die meisten Restautokorrelationen innerhalb der 95 %-Konfidenzbänder um Null liegen, die ungefähr +/- 2 auf der Quadratwurzel von n liegen, wobei n die Stichprobengröße ist. Sie können auch formal testen, ob diese Annahme erfüllt ist, indem Sie den Durbin-Watson-Test verwenden.

Was tun, wenn diese Annahme nicht respektiert wird?

Je nachdem, wie diese Annahme verletzt wird, haben Sie mehrere Möglichkeiten:

• Für eine positive serielle Korrelation sollten Sie erwägen, dem Modell Verzögerungen der abhängigen und/oder unabhängigen Variablen hinzuzufügen.
• Stellen Sie bei negativer serieller Korrelation sicher, dass keine Ihrer Variablen übermäßig verzögert ist.
• Für die saisonale Korrelation sollten Sie erwägen, dem Modell saisonale Dummies hinzuzufügen.

Hypothese 3: Homoskedastizität

Erläuterung

Die nächste Annahme der linearen Regression ist, dass die Residuen auf jeder Ebene von x eine konstante Varianz aufweisen. Dies nennt man Homoskedastizität . Wenn dies nicht der Fall ist, leiden die Residuen unter Heteroskedastizität .

Wenn in einer Regressionsanalyse Heteroskedastizität vorliegt, werden die Ergebnisse der Analyse schwer zu glauben. Insbesondere erhöht Heteroskedastizität die Varianz der Regressionskoeffizientenschätzungen, das Regressionsmodell berücksichtigt dies jedoch nicht. Dies macht es viel wahrscheinlicher, dass ein Regressionsmodell behauptet, ein Term im Modell sei statistisch signifikant, obwohl dies in Wirklichkeit nicht der Fall ist.

So ermitteln Sie, ob diese Annahme erfüllt ist

Der einfachste Weg, Heteroskedastizität zu erkennen, besteht darin, ein angepasstes Wert-/Residuendiagramm zu erstellen.

Sobald Sie eine Regressionslinie an einen Datensatz angepasst haben, können Sie ein Streudiagramm erstellen, das die angepassten Werte des Modells im Vergleich zu den Residuen dieser angepassten Werte zeigt. Das Streudiagramm unten zeigt ein typisches Diagramm des angepassten Werts gegenüber dem Residuum, in dem Heteroskedastizität vorhanden ist.

Beachten Sie, wie sich die Residuen mit zunehmenden angepassten Werten immer weiter ausbreiten. Diese „Kegelform“ ist ein klassisches Zeichen der Heteroskedastizität:

Was tun, wenn diese Annahme nicht respektiert wird?

Es gibt drei gängige Methoden zur Korrektur von Heteroskedastizität:

1. Transformieren Sie die abhängige Variable. Eine übliche Transformation besteht darin, einfach den Logarithmus der abhängigen Variablen zu verwenden. Wenn wir beispielsweise die Bevölkerungsgröße (unabhängige Variable) verwenden, um die Anzahl der Floristen in einer Stadt vorherzusagen (abhängige Variable), können wir stattdessen versuchen, die Bevölkerungsgröße zu verwenden, um den Logarithmus der Anzahl der Floristen in einer Stadt vorherzusagen. Die Verwendung des Protokolls der abhängigen Variablen anstelle der ursprünglichen abhängigen Variablen führt häufig dazu, dass die Heteroskedastizität verschwindet.

2. Definieren Sie die abhängige Variable neu. Eine übliche Methode zur Neudefinition der abhängigen Variablen besteht darin, eine Rate anstelle des Rohwerts zu verwenden. Anstatt beispielsweise die Bevölkerungsgröße zu verwenden, um die Anzahl der Floristen in einer Stadt vorherzusagen, können wir die Bevölkerungsgröße verwenden, um die Anzahl der Floristen pro Kopf vorherzusagen. In den meisten Fällen verringert sich dadurch die Variabilität, die natürlicherweise in größeren Populationen auftritt, da wir die Anzahl der Floristen pro Person messen und nicht die Anzahl der Floristen selbst.

3. Verwenden Sie eine gewichtete Regression. Eine andere Möglichkeit zur Korrektur der Heteroskedastizität ist die Verwendung einer gewichteten Regression. Diese Art der Regression weist jedem Datenpunkt basierend auf der Varianz seines angepassten Werts eine Gewichtung zu. Im Wesentlichen werden dadurch Datenpunkte mit höheren Varianzen niedrig gewichtet, wodurch ihre Restquadrate reduziert werden. Durch die Verwendung geeigneter Gewichte kann das Problem der Heteroskedastizität beseitigt werden.

Hypothese 4: Normalität

Erläuterung

Die nächste Annahme der linearen Regression ist, dass die Residuen normalverteilt sind.

So ermitteln Sie, ob diese Annahme erfüllt ist

Es gibt zwei gängige Methoden, um zu überprüfen, ob diese Annahme erfüllt ist:

1. Überprüfen Sie die Hypothese visuell mithilfe von QQ-Plots .

Ein QQ-Diagramm, kurz für Quantil-Quantil-Diagramm, ist eine Art Diagramm, mit dem wir bestimmen können, ob die Residuen eines Modells einer Normalverteilung folgen oder nicht. Wenn die Punkte auf dem Diagramm ungefähr eine gerade diagonale Linie bilden, ist die Normalitätsannahme erfüllt.

Das folgende QQ-Diagramm zeigt ein Beispiel für Residuen, die ungefähr einer Normalverteilung folgen:

Das folgende QQ-Diagramm zeigt jedoch ein Beispiel für einen Fall, in dem die Residuen deutlich von einer geraden diagonalen Linie abweichen, was darauf hindeutet, dass sie nicht der Normalverteilung folgen:

2. Sie können die Normalitätsannahme auch mithilfe formaler statistischer Tests wie Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre oder D’Agostino-Pearson überprüfen. Beachten Sie jedoch, dass diese Tests empfindlich auf große Stichprobengrößen reagieren – das heißt, sie kommen häufig zu dem Schluss, dass die Residuen nicht normal sind, wenn die Stichprobengröße groß ist. Aus diesem Grund ist es oft einfacher, einfach grafische Methoden wie einen QQ-Plot zu verwenden, um diese Hypothese zu überprüfen.

Was tun, wenn diese Annahme nicht respektiert wird?

Wenn die Normalitätsannahme nicht erfüllt ist, haben Sie mehrere Möglichkeiten:

• Überprüfen Sie zunächst, ob die Ausreißer keinen großen Einfluss auf die Verteilung haben. Wenn es Ausreißer gibt, stellen Sie sicher, dass es sich um echte Werte und nicht um Dateneingabefehler handelt.
• Anschließend können Sie eine nichtlineare Transformation auf die unabhängige und/oder abhängige Variable anwenden. Gängige Beispiele sind die Berechnung des Logarithmus, der Quadratwurzel oder des Kehrwerts der unabhängigen und/oder abhängigen Variablen.

Weiterführende Literatur:

Einführung in die einfache lineare Regression
Heteroskedastizität in der Regressionsanalyse verstehen
So erstellen und interpretieren Sie ein QQ-Diagramm in R