Links- oder rechtsschiefe verteilungen

Schiefe ist eine Möglichkeit, die Symmetrie einer Verteilung zu beschreiben.

Eine Verteilung ist schief , wenn sie auf der linken Seite der Verteilung einen „Schwanz“ hat:

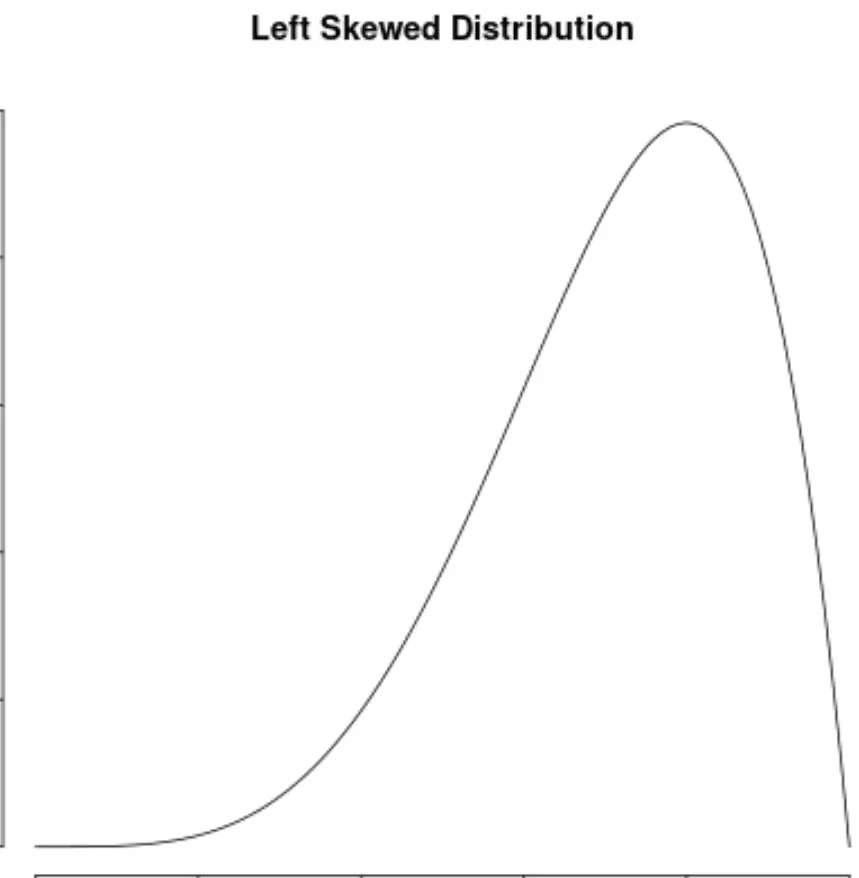
Eine Verteilung ist rechtsschief , wenn sie auf der rechten Seite der Verteilung einen „Schwanz“ hat:

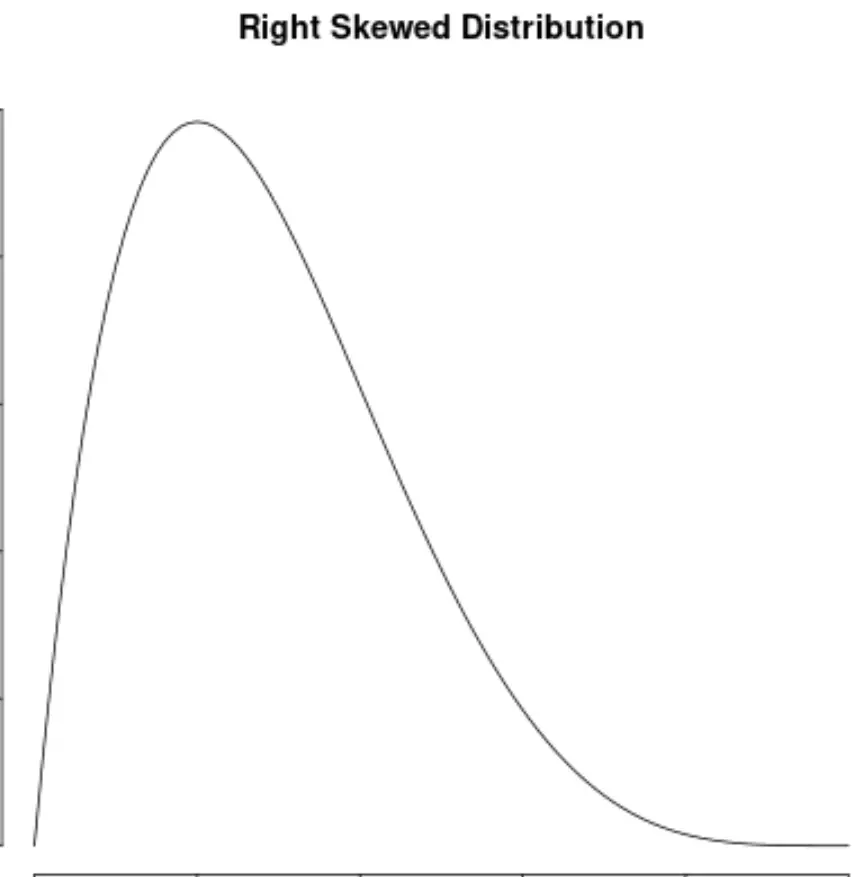
Und eine Verteilung hat keinen Bias, wenn sie auf beiden Seiten symmetrisch ist:

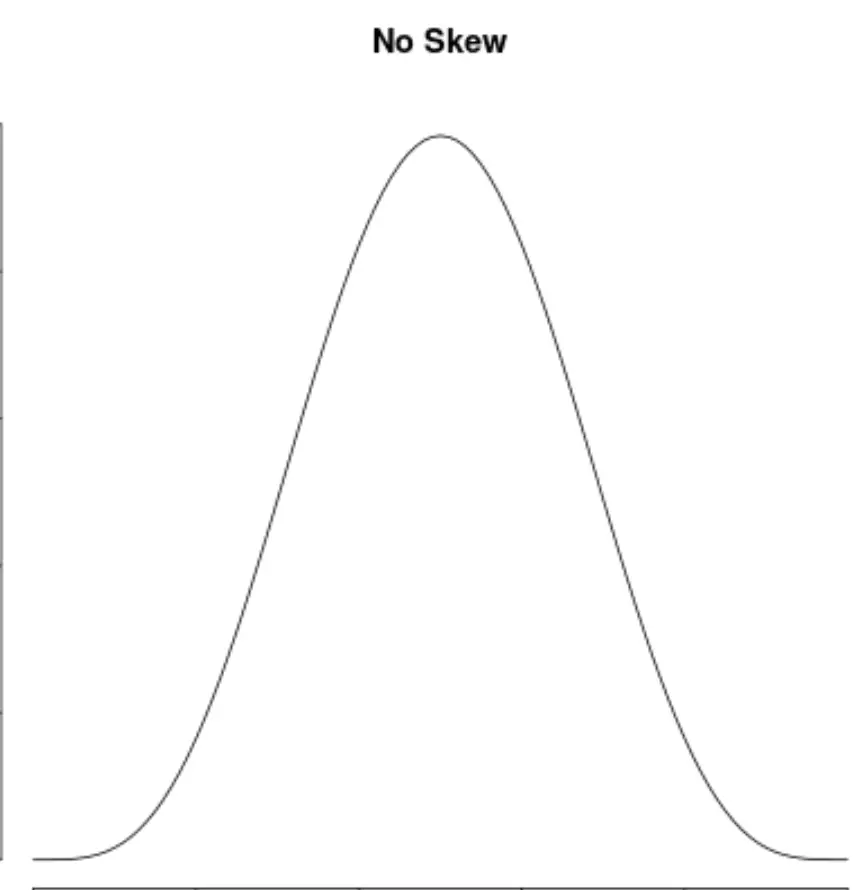
Beachten Sie, dass linksschiefe Verteilungen manchmal als „negativ schiefe“ Verteilungen und rechtsschiefe Verteilungen manchmal als „positiv schiefe“ Verteilungen bezeichnet werden.

Eigenschaften schiefer Verteilungen

Die folgenden Diagramme zeigen, wo Mittelwert, Median und Modus typischerweise in verschiedenen Verteilungen liegen.

Linksschiefe Verteilung: Mittelwert < Median < Modus

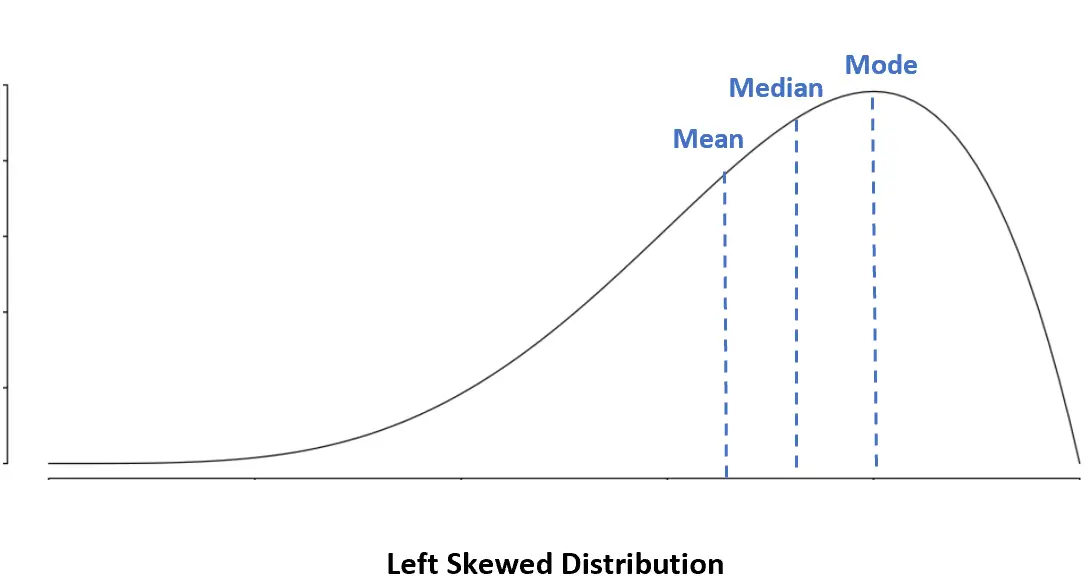
Bei einer linksschiefen Verteilung ist der Mittelwert kleiner als der Median.

Rechtsschiefe Verteilung: Modus < Median < Mittel

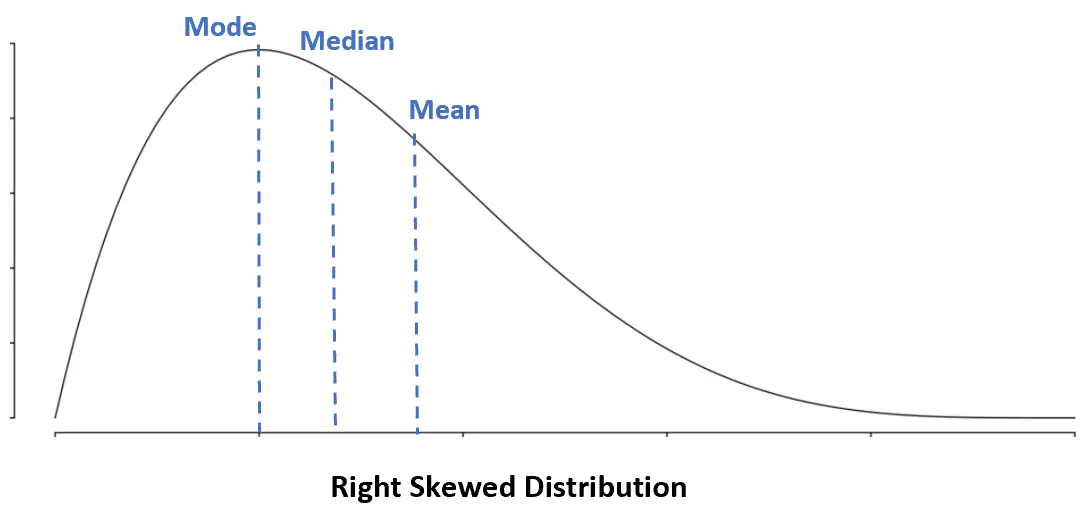
Bei einer rechtsschiefen Verteilung ist der Mittelwert größer als der Median.

Keine Verzerrung: Mittelwert = Median = Modus

Bei einer symmetrischen Verteilung sind Mittelwert, Median und Modus alle gleich.

Verwendung von Boxplots zur Visualisierung von Asymmetrie

Ein Boxplot ist eine Art Diagramm, das die fünfstellige Zusammenfassung eines Datensatzes anzeigt, der Folgendes umfasst:

• Der Mindestwert
• Das erste Quartil (das 25. Perzentil)
• Der Medianwert
• Das dritte Quartil (das 75. Perzentil)
• Der Maximalwert

Um ein Boxplot zu erstellen, zeichnen wir eine Box vom ersten bis zum dritten Quartil. Als nächstes zeichnen wir eine vertikale Linie am Mittelwert. Abschließend zeichnen wir „Whisker“ der Quartile bis zum Minimal- und Maximalwert.

Anhand der Position des Medianwerts im Boxplot können wir bestimmen, ob eine Verteilung linksschief, rechtsschief oder symmetrisch ist.

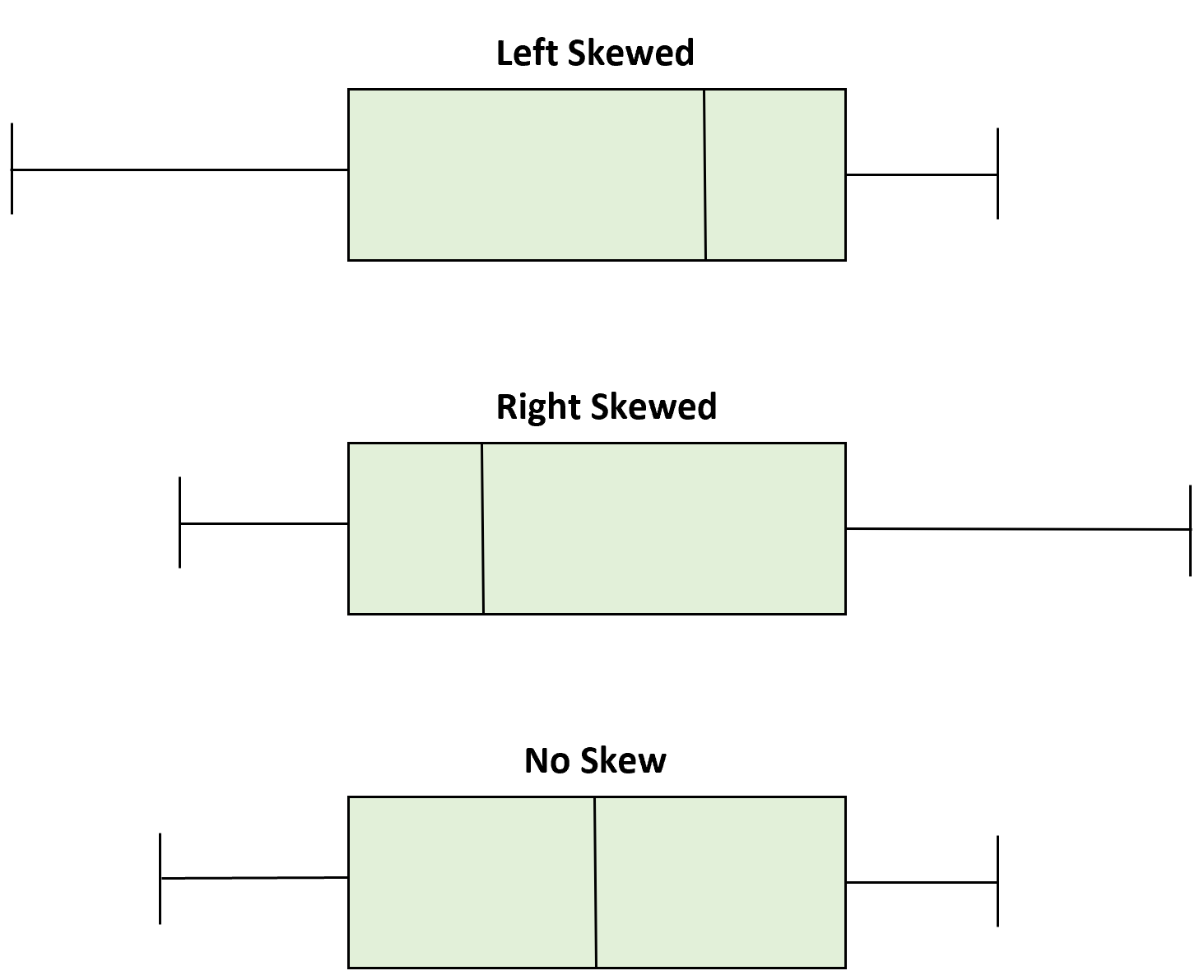
Wenn der Median näher am Boden der Box liegt und der Whisker am unteren Ende der Box kürzer ist, ist die Verteilung rechtsschief.

Wenn der Median näher am oberen Rand des Kastens liegt und der Whisker am oberen Ende des Kastens kürzer ist, bleibt die Verteilung schief.

Wenn der Median in der Mitte der Box liegt und die Whiskers auf jeder Seite ungefähr gleich sind, ist die Verteilung symmetrisch.

Beispiele für schiefe Verteilungen

Hier sind einige konkrete Beispiele für schiefe Verteilungen.

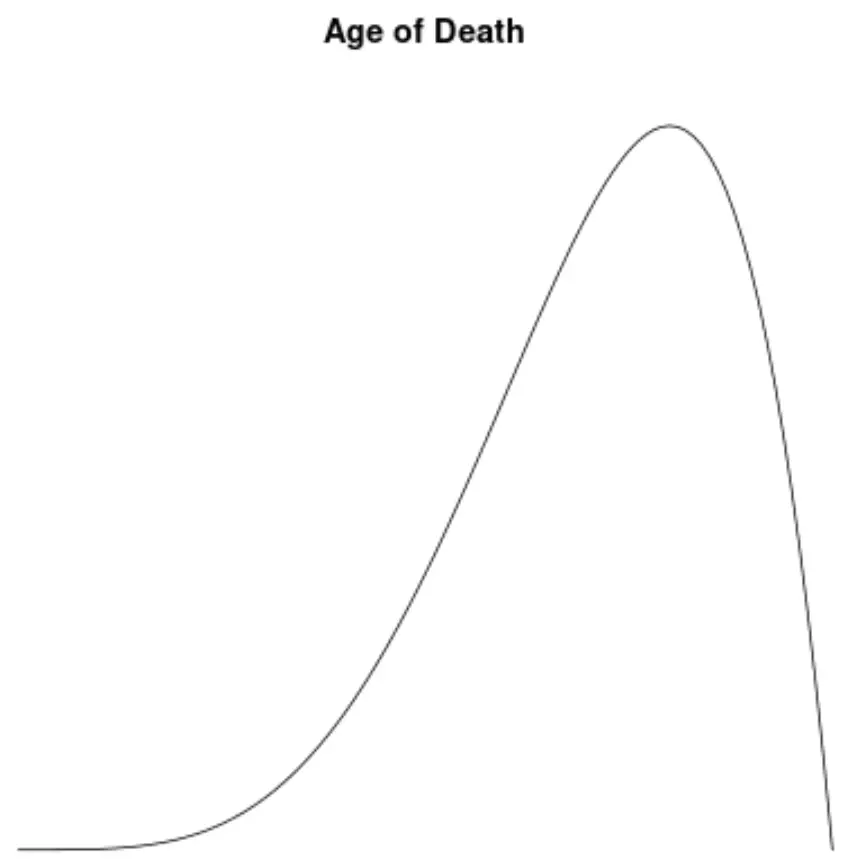
Linksschiefe Verteilung: die Verteilung des Sterbealters.

Die Altersverteilung der Todesfälle ist in den meisten Bevölkerungsgruppen linksschief. Die meisten Menschen leben zwischen 70 und 80 Jahren, und immer weniger leben darunter.

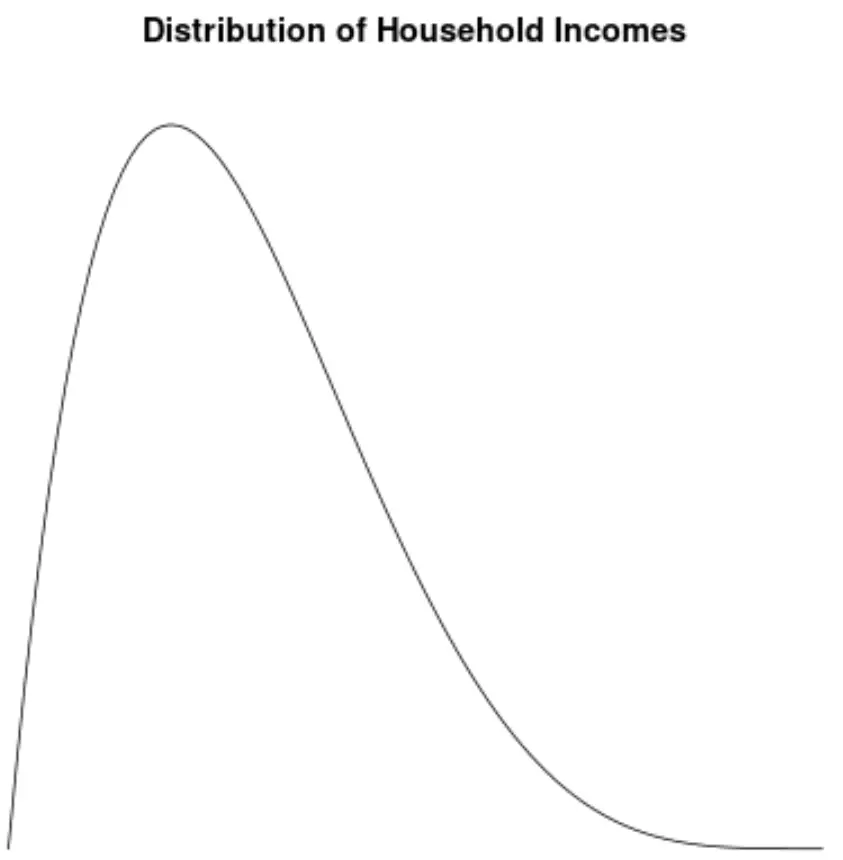
Rechtsschiefe Verteilung: die Verteilung des Haushaltseinkommens.

Die Verteilung des Haushaltseinkommens in den Vereinigten Staaten ist rechtsschief, wobei die meisten Haushalte zwischen 40.000 und 80.000 US-Dollar pro Jahr verdienen, aber eine lange rechte Ecke der Haushalte verdient viel mehr.

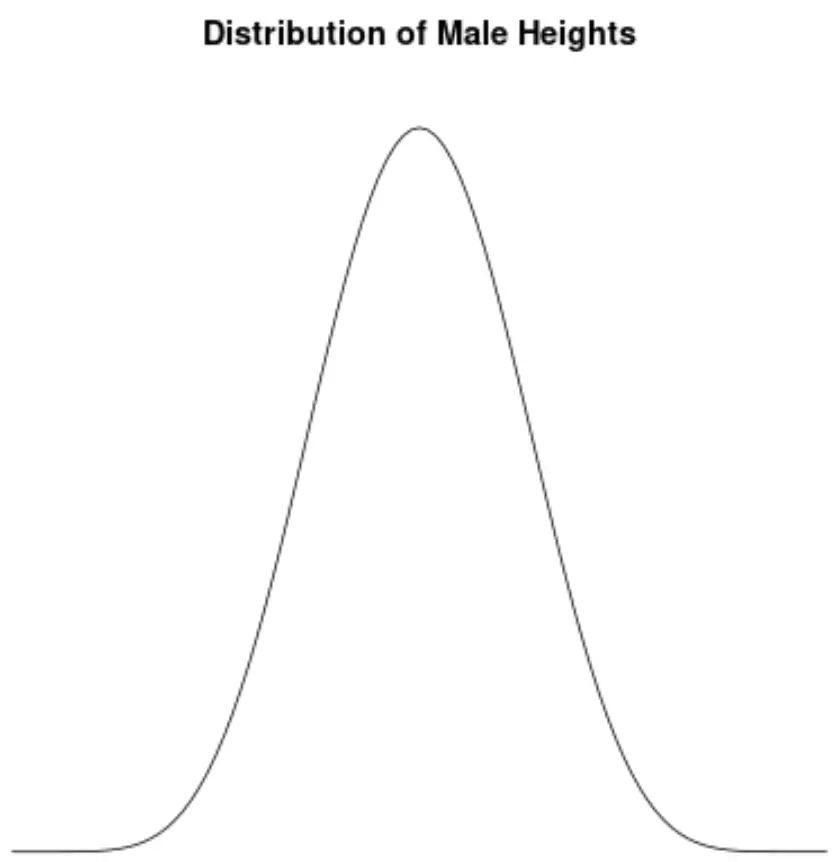
Kein Skew: die Verteilung männlicher Größen.

Es ist bekannt, dass die Größe der Männchen ungefähr normal ist und keine Asymmetrie aufweist. Beispielsweise beträgt die durchschnittliche Größe eines Mannes in den Vereinigten Staaten etwa 69,1 Zoll. Die Höhenverteilung ist ungefähr symmetrisch, wobei einige kürzer und andere höher sind.

Zusätzliche Ressourcen

5 Beispiele für positiv verzerrte Verteilungen
5 Beispiele für negativ verzerrte Verteilungen
So berechnen Sie die Schiefe in Excel
So identifizieren Sie Asymmetrie in Boxplots