So verwenden sie die funktion lm() in r, um lineare modelle anzupassen

Die Funktion lm() in R wird verwendet, um lineare Regressionsmodelle anzupassen.

Diese Funktion verwendet die folgende grundlegende Syntax:

lm(Formel, Daten, …)

Gold:

• Formel: Die lineare Modellformel (z. B. y ~ x1 + x2)
• Daten: Der Name des Datenblocks, der die Daten enthält

Das folgende Beispiel zeigt, wie Sie diese Funktion in R verwenden, um Folgendes zu tun:

• Passen Sie ein Regressionsmodell an
• Zusammenfassung der Anpassung des Regressionsmodells anzeigen
• Modelldiagnosediagramme anzeigen
• Stellen Sie das angepasste Regressionsmodell grafisch dar
• Treffen Sie Vorhersagen mithilfe des Regressionsmodells

Passen Sie das Regressionsmodell an

Der folgende Code zeigt, wie die Funktion lm() verwendet wird, um ein lineares Regressionsmodell in R anzupassen:

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

Zusammenfassung des Regressionsmodells anzeigen

Anschließend können wir die Funktion summary() verwenden, um die Zusammenfassung der Anpassung des Regressionsmodells anzuzeigen:

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

So interpretieren Sie die wichtigsten Werte im Modell:

• F-Statistik = 18,35, entsprechender p-Wert = 0,002675. Da dieser p-Wert kleiner als 0,05 ist, ist das Modell insgesamt statistisch signifikant.
• Vielfaches R im Quadrat = 0,6964. Dies zeigt uns, dass 69,64 % der Variation der Antwortvariablen y durch die Prädiktorvariable x erklärt werden können.
• Geschätzter Koeffizient von x : 1,2780. Dies sagt uns, dass jede weitere Erhöhung von x um eine Einheit mit einem durchschnittlichen Anstieg von 1,2780 in y verbunden ist.

Anschließend können wir die Koeffizientenschätzungen aus der Ausgabe verwenden, um die geschätzte Regressionsgleichung zu schreiben:

y = 11,1432 + 1,2780*(x)

Bonus : Eine vollständige Anleitung zur Interpretation der einzelnen Werte der Regressionsausgabe in R finden Sie hier .

Modelldiagnosediagramme anzeigen

Anschließend können wir die Funktion plot() verwenden, um die Diagnosediagramme des Regressionsmodells darzustellen:

 #create diagnostic plots
plot(model) 

Mithilfe dieser Diagramme können wir die Residuen des Regressionsmodells analysieren, um festzustellen, ob das Modell für die Daten geeignet ist.

In diesem Tutorial finden Sie eine vollständige Erklärung zur Interpretation der Diagnosediagramme eines Modells in R.

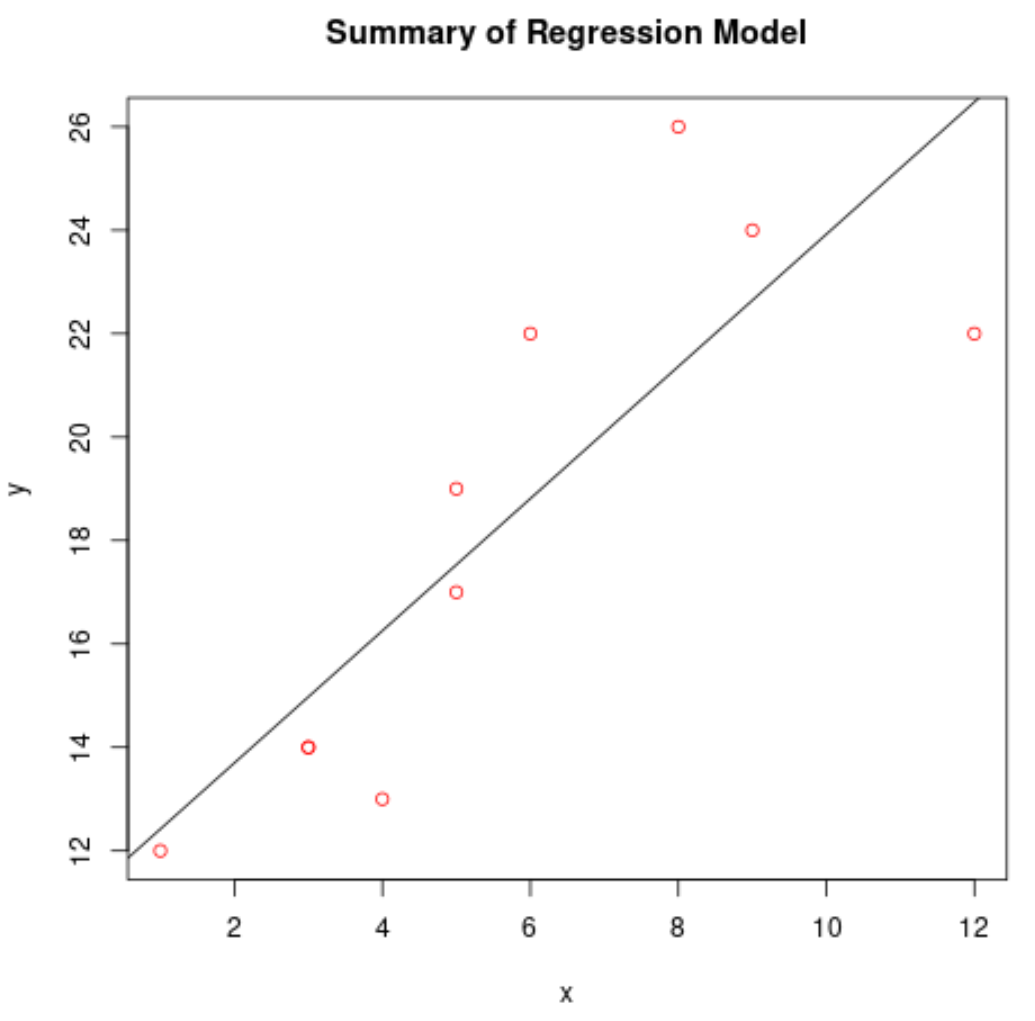
Stellen Sie das angepasste Regressionsmodell grafisch dar

Wir können die Funktion abline() verwenden, um das angepasste Regressionsmodell darzustellen:

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

Verwenden Sie das Regressionsmodell, um Vorhersagen zu treffen

Wir können die Funktion Predict() verwenden, um den Antwortwert für eine neue Beobachtung vorherzusagen:

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

Das Modell sagt voraus, dass diese neue Beobachtung einen Antwortwert von 17,5332 haben wird.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine schrittweise Regression in R durch