So führen sie einen log-rank-test in r durch

Ein Log-Rank-Test ist die gebräuchlichste Methode, um Überlebenskurven zwischen zwei Gruppen zu vergleichen.

Dieser Test basiert auf den folgenden Annahmen :

H ₀ : Es gibt keinen Unterschied im Überleben zwischen den beiden Gruppen.

H _A : Es gibt einen Unterschied im Überleben zwischen den beiden Gruppen.

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), können wir die Nullhypothese ablehnen und daraus schließen, dass genügend Beweise dafür vorliegen, dass zwischen den beiden Gruppen ein Unterschied im Überleben besteht.

Um einen Log-Rank-Test in R durchzuführen, können wir die Funktion survdiff() aus dem Survival- Paket verwenden, die die folgende Syntax verwendet:

survdiff(Surv(time, status) ~ Prädiktoren, Daten)

Diese Funktion gibt eine Chi-Quadrat-Teststatistik und einen entsprechenden p-Wert zurück.

Das folgende Beispiel zeigt, wie Sie diese Funktion verwenden, um einen Log-Rank-Test in R durchzuführen.

Beispiel: Log-Rank-Test in R

Für dieses Beispiel verwenden wir den Eierstockdatensatz aus dem Survival- Paket. Dieser Datensatz enthält die folgenden Informationen zu 26 Patienten:

• Überlebenszeit (in Monaten) nach der Diagnose Eierstockkrebs
• Ob die Überlebenszeit zensiert wurde oder nicht
• Art der erhaltenen Behandlung (rx = 1 oder rx = 2)

Der folgende Code zeigt, wie die ersten sechs Zeilen dieses Datensatzes angezeigt werden:

 library (survival)

#view first six rows of dataset
head(ovarian)

  futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5,431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2

Der folgende Code zeigt, wie ein Log-Rank-Test durchgeführt wird, um festzustellen, ob es einen Unterschied im Überleben zwischen Patienten gibt, die unterschiedliche Behandlungen erhalten haben:

 #perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)

Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)

      N Observed Expected (OE)^2/E (OE)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06

 Chisq= 1.1 on 1 degrees of freedom, p= 0.3 

Die Chi-Quadrat-Teststatistik beträgt 1,1 mit 1 Freiheitsgrad und der entsprechende p-Wert beträgt 0,3 . Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Mit anderen Worten: Wir haben keine ausreichenden Beweise dafür, dass es einen statistisch signifikanten Unterschied im Überleben zwischen den beiden Behandlungen gibt.

Wir können auch Überlebenskurven für jede Gruppe zeichnen, indem wir die folgende Syntax verwenden:

 #plot survival curves for each treatment group
plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian), 
     xlab = " Time ", 
     ylab = “ Overall survival probability ”)

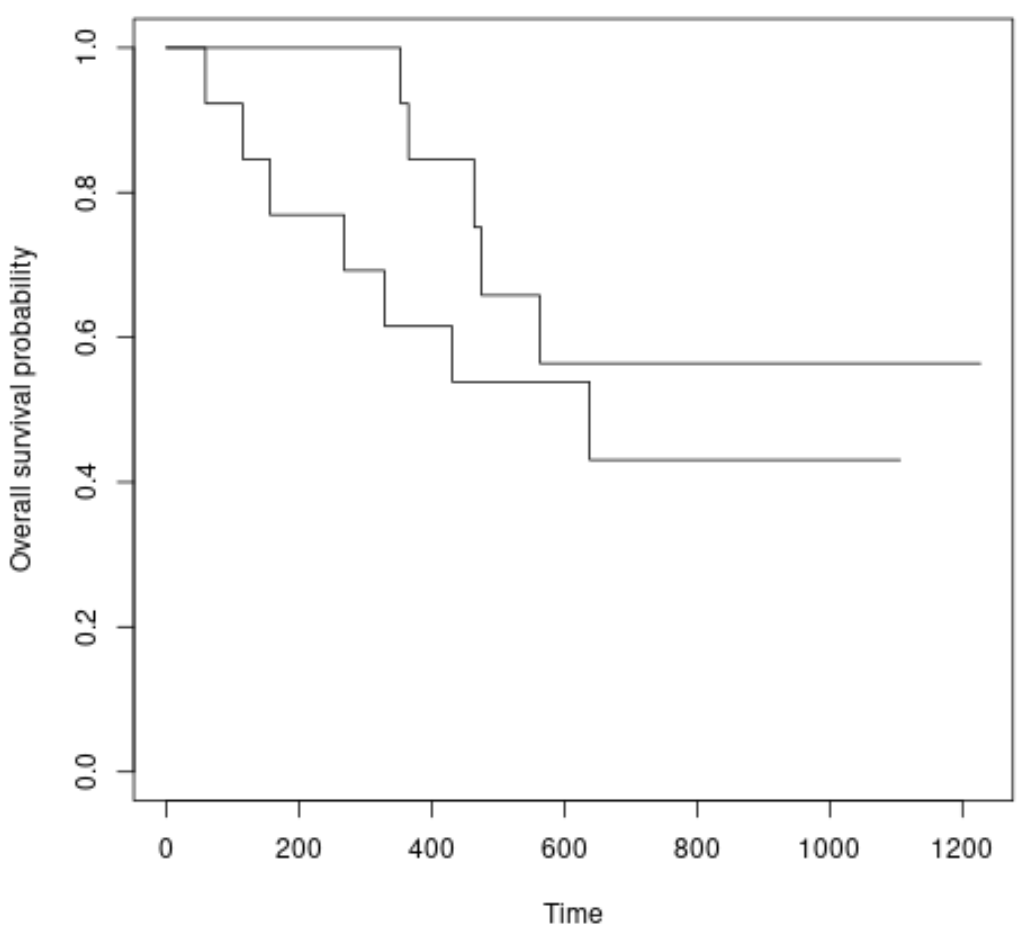
Wir können sehen, dass die Überlebenskurven leicht unterschiedlich sind, aber der Log-Rank-Test hat uns gezeigt, dass der Unterschied statistisch nicht signifikant ist.