Lognormalverteilung
In diesem Artikel wird erläutert, was die Lognormalverteilung in der Statistik ist. Sie erfahren also, welche Eigenschaften die Lognormalverteilung und der Graph dieser Art von Wahrscheinlichkeitsverteilung haben.
Was ist die Lognormalverteilung?
Die Lognormalverteilung oder Lognormalverteilung ist eine Wahrscheinlichkeitsverteilung, die eine Zufallsvariable definiert, deren Logarithmus einer Normalverteilung folgt.
Wenn also die Variable X eine Normalverteilung hat, dann hat die Exponentialfunktion e x eine Lognormalverteilung.
Beachten Sie, dass die Lognormalverteilung nur verwendet werden kann, wenn die Variablenwerte positiv sind, da der Logarithmus eine Funktion ist, die nur ein positives Argument akzeptiert.
Unter den verschiedenen Anwendungen der Lognormalverteilung in der Statistik unterscheiden wir die Verwendung dieser Verteilung zur Analyse von Finanzinvestitionen und zur Durchführung von Zuverlässigkeitsanalysen.
Die Lognormalverteilung wird auch als Tinaut-Verteilung bezeichnet, manchmal auch als Lognormalverteilung oder Log-Normalverteilung geschrieben.
Diagramm der Lognormalverteilung
Nachdem wir nun die Definition der Lognormalverteilung kennen, werden wir in diesem Abschnitt sehen, wie die grafische Darstellung der Lognormalverteilung abhängig von den Werten ihres arithmetischen Mittels und ihrer Standardabweichung variiert.
Der Graph der Dichtefunktion der Lognormalverteilung sieht wie folgt aus:
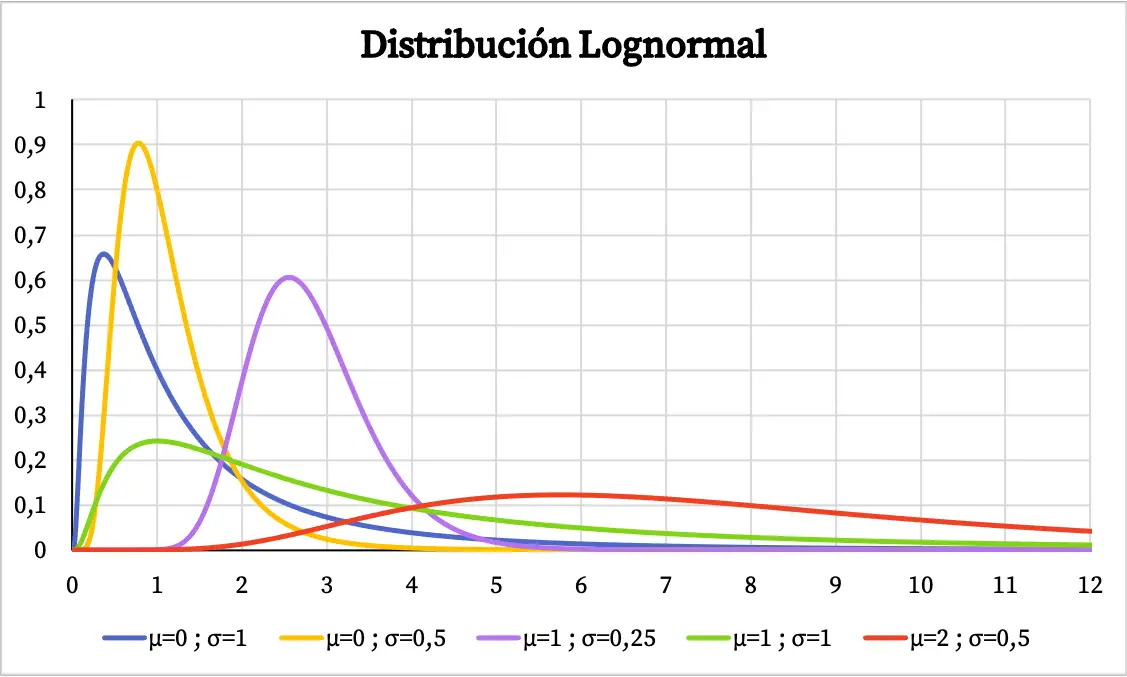
Andererseits sieht das kumulative Wahrscheinlichkeitsdiagramm der Lognormalverteilung wie folgt aus:
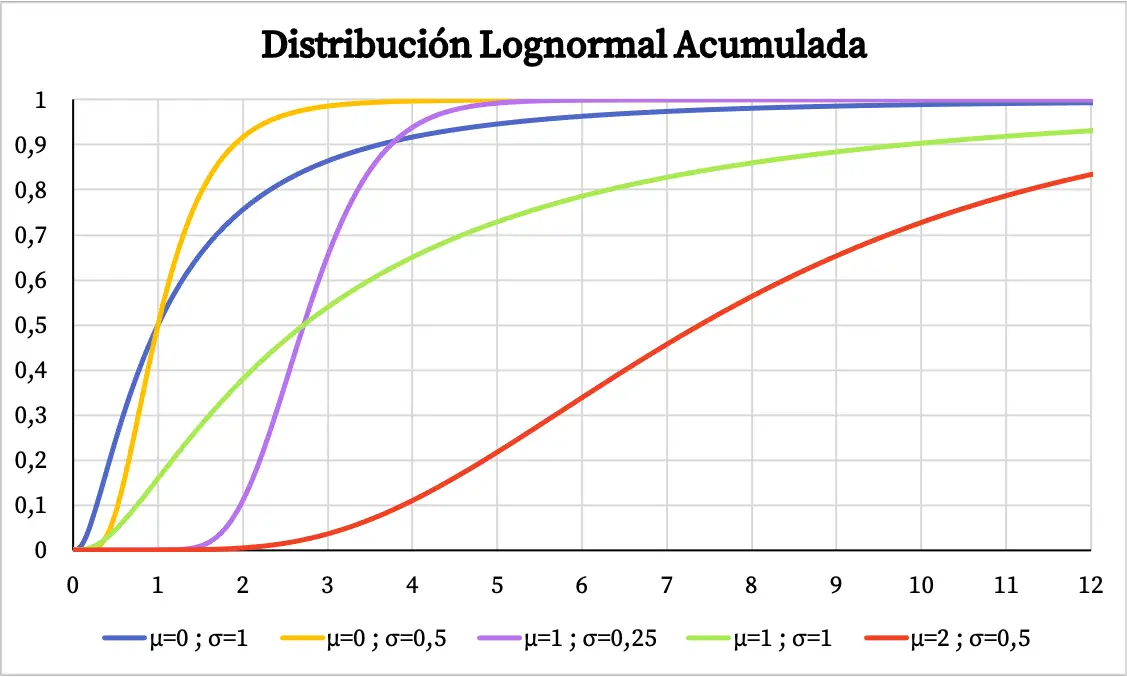
Merkmale der Lognormalverteilung
Die Lognormalverteilung weist die folgenden Merkmale auf:
- Die Lognormalverteilung wird durch den Wert zweier Parameter definiert, ihr arithmetisches Mittel μ und ihre Varianz σ 2 .
- Der Bereich der Lognormalverteilung besteht aus positiven reellen Zahlen, da der Logarithmus keine negativen oder Nullwerte akzeptiert.
- Der Erwartungswert einer logarithmischen Normalverteilung ist gleich der Zahl e, erhöht um die Summe aus Mittelwert plus Varianz dividiert durch zwei.
![\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-109a1024d530b2993db41f1d7a5a24c3_l3.png "Rendered by QuickLaTeX.com")
- Andererseits kann die Varianz einer Lognormalverteilung mit dem folgenden Ausdruck berechnet werden:
- Der Modus der Lognormalverteilung entspricht der Zahl e erhöht auf den Mittelwert der Verteilung.
- Der Schiefekoeffizient der Lognormalverteilung kann durch Anwendung der folgenden Formel bestimmt werden:
- Die Formel für die Dichtefunktion der Lognormalverteilung lautet:
![\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)](https://statorials.org/wp-content/ql-cache/quicklatex.com-25698732745689402d16ea353a072cc1_l3.png "Rendered by QuickLaTeX.com")
- Die Formel für die kumulative Wahrscheinlichkeitsfunktion der Lognormalverteilung lautet:
![\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)](https://statorials.org/wp-content/ql-cache/quicklatex.com-59c2474703bad4805a6a44bd05cf92bd_l3.png "Rendered by QuickLaTeX.com")
Gold
ist die kumulative Wahrscheinlichkeitsfunktion einer Standardnormalverteilung .
- Das arithmetische Mittel einer Lognormalverteilung ist größer als der Wert ihres Medians.
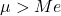
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen