Logarithmische regression

In diesem Artikel wird erklärt, was logarithmische Regression ist und wie sie durchgeführt wird. Darüber hinaus können Sie sich ein Beispiel einer logarithmischen Regression ansehen, um das Konzept vollständig zu verstehen.

Was ist eine logarithmische Regression?

Die logarithmische Regression ist ein Regressionsmodell, das einen Logarithmus in seine Gleichung einbezieht. Konkret wird bei einer logarithmischen Regression der Logarithmus der unabhängigen Variablen genommen. Die Gleichung für ein logarithmisches Regressionsmodell lautet also y=a+b·ln(x).

Die logarithmische Regression ist sehr nützlich für die Anpassung eines Regressionsmodells, wenn die Beispieldaten eine logarithmische Kurve bilden, sodass das Regressionsmodell besser an die Beispieldaten passt. Nachfolgend erfahren Sie, wann Sie eine logarithmische Regression durchführen sollten.

Somit ist die logarithmische Regression eine Art nichtlineare Regression, genau wie die exponentielle Regression und die polynomielle Regression.

Logarithmische Regressionsformel

Bei einem logarithmischen Regressionsmodell wird der Logarithmus der unabhängigen Variablen gebildet. Daher lautet die Formel für die Gleichung einer logarithmischen Regression y=a+b·ln(x).

Gold:

• 

  ist die abhängige Variable.

• 

  ist die unabhängige Variable.

• 

  sind die Regressionskoeffizienten.

Beachten Sie, dass y=a+b·ln(x) eigentlich die Gleichung einer Geraden ist, sich aber nicht auf die ursprünglichen Variablen x und y, sondern auf die Variablen ln(x) und y bezieht.

Wann sollte eine logarithmische Regression durchgeführt werden?

Wir müssen eine logarithmische Regression durchführen, wenn der Graph der Beispieldaten eine logarithmische Kurve ist, das heißt, wenn die Darstellung der Punkte dem Graphen einer logarithmischen Funktion ähnelt.

Schauen Sie sich das Streudiagramm unten an. Ein lineares Regressionsmodell wurde an einen Datensatz angepasst. Wie Sie sehen, stellt die Linie keine schlechte Annäherung an die Daten dar. Wenn Sie jedoch vorsichtig sind, steigen die Werte am Anfang des Diagramms schneller an als am Ende, sodass die Linie nicht vollständig mit den Beobachtungen übereinstimmt .

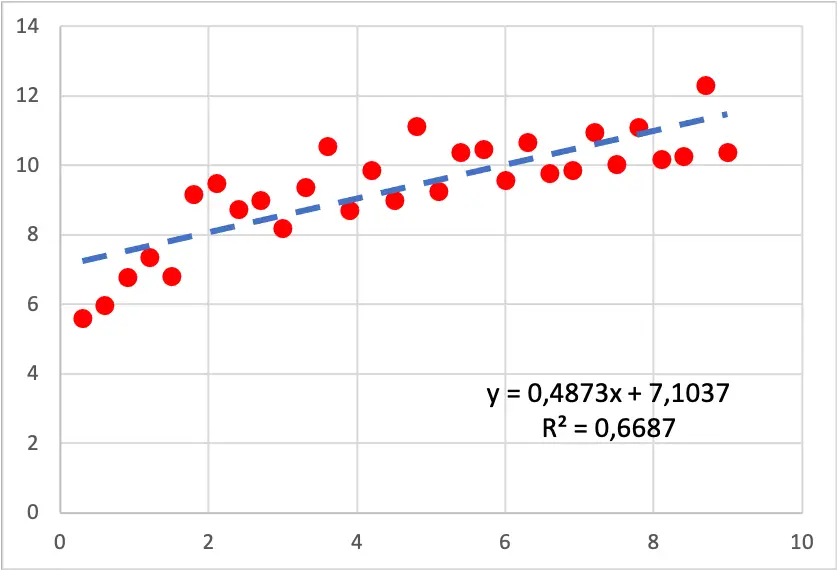
Es lohnt sich also, ein logarithmisches Regressionsmodell zu erstellen, da es so aussieht, als ob die Daten einer logarithmischen Kurve folgen. Das aus dem logarithmischen Regressionsmodell erhaltene Ergebnis lautet wie folgt:

Wie Sie in der vorherigen Grafik sehen können, passt das resultierende logarithmische Regressionsmodell besser zu den Beispieldaten. Tatsächlich stieg das Bestimmtheitsmaß von 66,87 % auf 80,05 %, sodass das Modell die Datenstichprobe nun besser erklären kann. Daher ist es in diesem Fall besser, die logistische Regression zu verwenden, um eine Gleichung zu finden, die den Datenwert annähert.

Andere Arten der nichtlinearen Regression

Die drei häufigsten Fälle nichtlinearer Regression sind:

• Logarithmische Regression : Der Logarithmus der unabhängigen Variablen wird genommen.
• Exponentielle Regression : Die unabhängige Variable ist der Exponent der Gleichung.
• Polynomielle Regression : Die Gleichung des Regressionsmodells liegt in Form eines Polynoms vor.