So verwenden sie die logest-funktion in excel (mit beispiel)

Sie können die LOGEST- Funktion in Excel verwenden, um die Formel für eine Exponentialkurve zu berechnen, die zu Ihren Daten passt.

Die Gleichung der Kurve wird die folgende Form annehmen:

y = b* ^mx

Diese Funktion verwendet die folgende grundlegende Syntax:

 = LOGEST ( known_y's, [known_x's], [const], [stats] )

Gold:

• bekannte_y’s : ein Array bekannter y-Werte
• known_x’s : ein Array bekannter x-Werte
• const : Optionales Argument. Wenn TRUE, wird Konstante b normal verarbeitet. Bei FALSE wird die Konstante b auf 1 gesetzt.
• Statistiken : Optionales Argument. Bei TRUE werden zusätzliche Regressionsstatistiken zurückgegeben. Bei FALSE werden keine zusätzlichen Regressionsstatistiken zurückgegeben.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie diese Funktion in der Praxis nutzen.

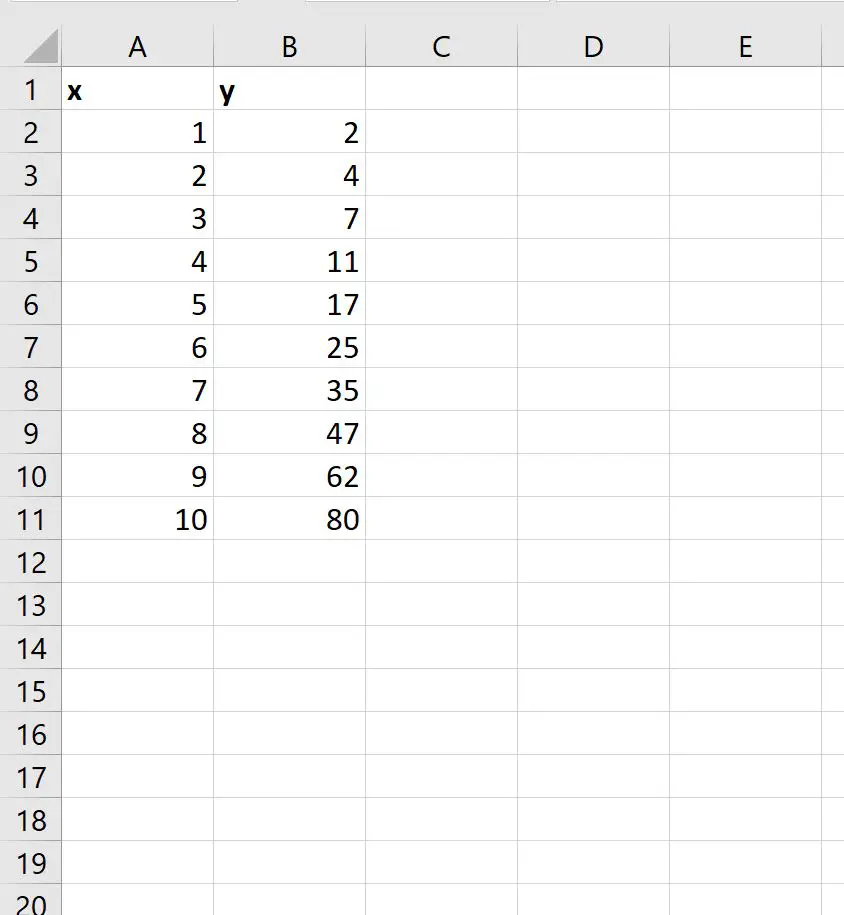
Schritt 1: Geben Sie die Daten ein

Geben wir zunächst den folgenden Datensatz in Excel ein:

Schritt 2: Visualisieren Sie die Daten

Als Nächstes erstellen wir ein schnelles Streudiagramm von x gegenüber y, um zu überprüfen, ob die Daten tatsächlich einer Exponentialkurve folgen:

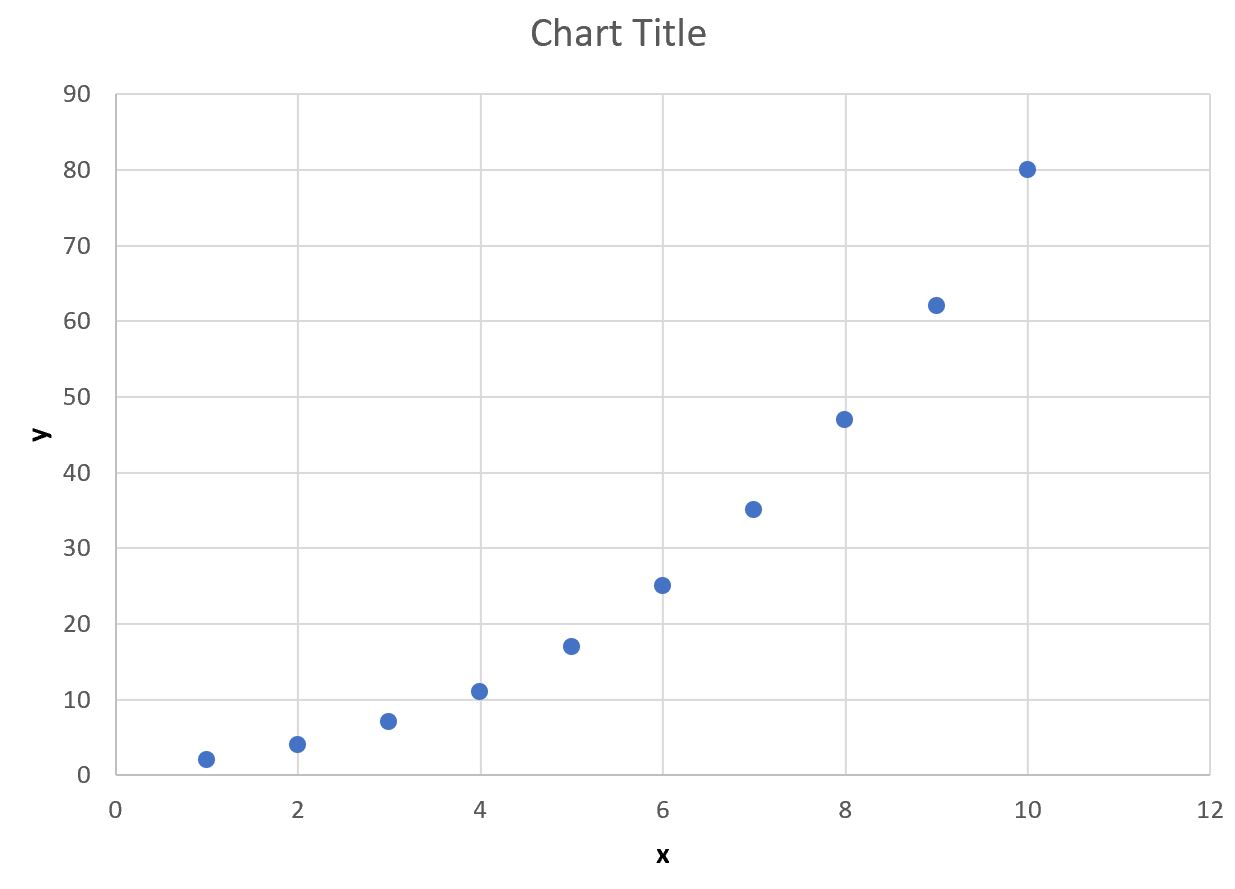
Wir können sehen, dass die Daten tatsächlich einer Exponentialkurve folgen.

Schritt 3: Verwenden Sie LOGEST, um die Formel für die Exponentialkurve zu finden

Dann können wir die folgende Formel in eine beliebige Zelle eingeben, um die Exponentialkurvenformel zu berechnen:

 =LOGEST( B2:B11 , A2:A11 )

Der folgende Screenshot zeigt, wie diese Formel in der Praxis angewendet wird:

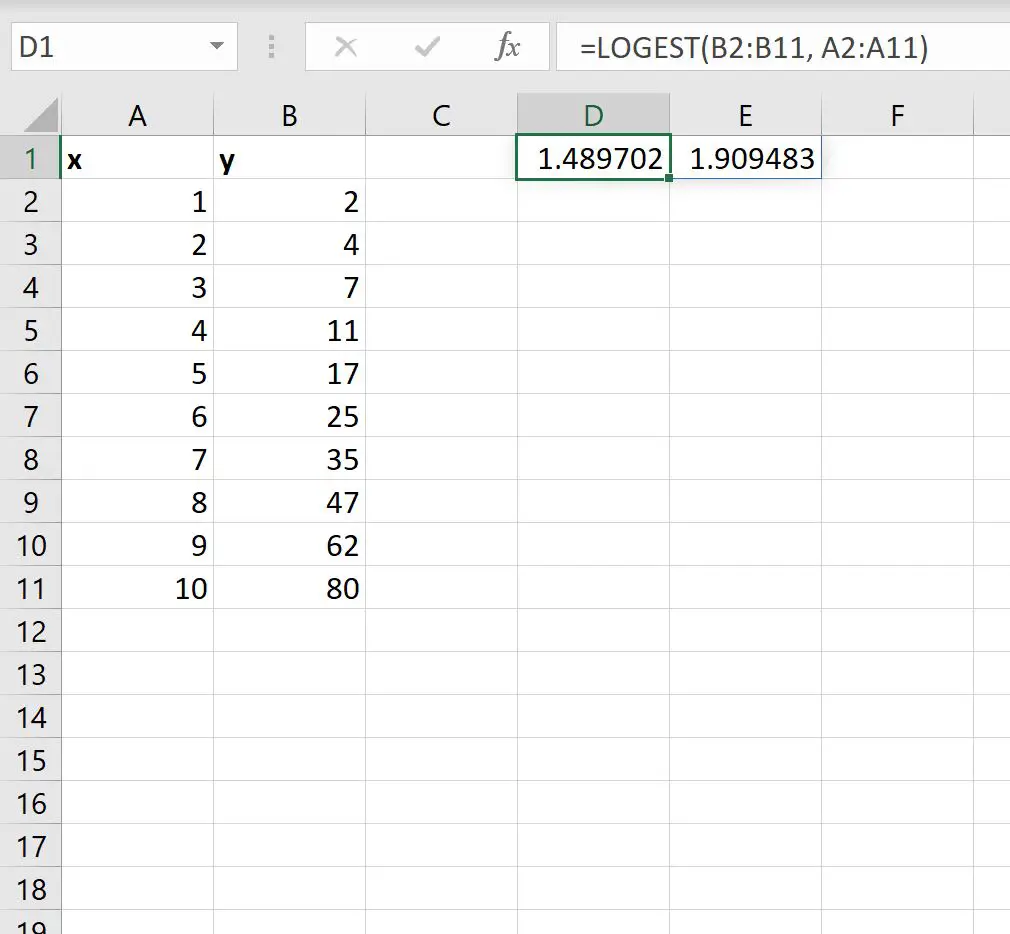
Der erste Wert der Ausgabe repräsentiert den Wert von m und der zweite Wert der Ausgabe repräsentiert den Wert von b in der Gleichung:

y = b* ^mx

Wir würden diese Exponentialkurvenformel also wie folgt schreiben:

y = 1,909483 * ^1,489702x

Wir könnten diese Formel dann verwenden, um die Werte von y basierend auf dem Wert von x vorherzusagen.

Wenn xa beispielsweise einen Wert von 8 hat, sagen wir voraus, dass y einen Wert von 46,31 hat:

y = 1,909483 * 1,489702 · ⁸ = 46,31

Schritt 4 (optional): Sehen Sie sich zusätzliche Regressionsstatistiken an

Wir können den Wert des Stats- Arguments in der LOGEST- Funktion auf TRUE setzen, um zusätzliche Regressionsstatistiken für die angepasste Regressionsgleichung anzuzeigen:

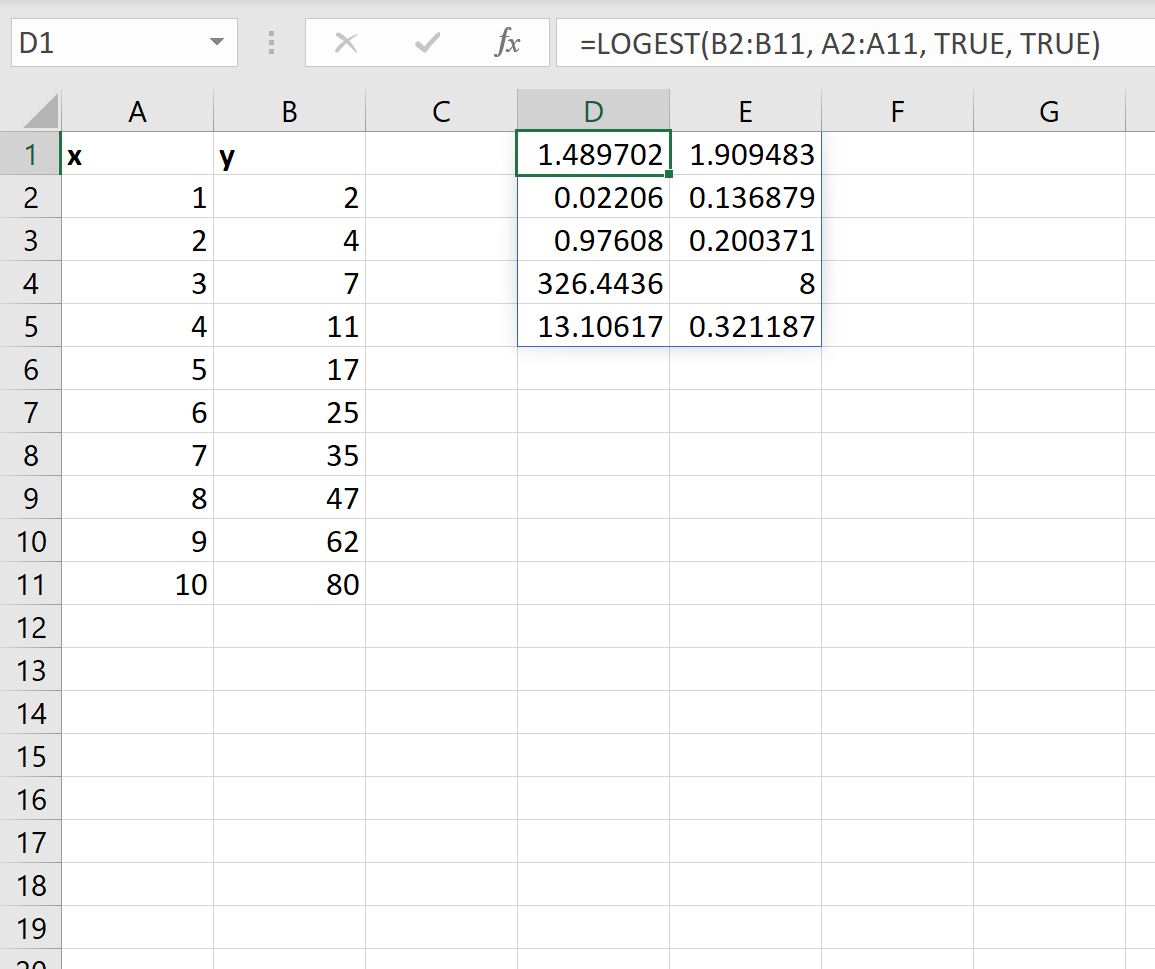
So interpretieren Sie jeden Wert im Ergebnis:

• Der Standardfehler für m beträgt 0,02206 .
• Der Standardfehler für b beträgt 0,136879 .
• Der R ² des Modells beträgt .97608 .
• Der Standardfehler für y beträgt .200371 .
• Die F-Statistik ist 326,4436 .
• Die Freiheitsgrade betragen 8 .
• Die Regressionsquadratsumme beträgt 13,10617 .
• Die verbleibende Quadratsumme beträgt .321187 .

Im Allgemeinen ist das Maß von größtem Interesse in diesen zusätzlichen Statistiken der R ² -Wert, der den Anteil der Varianz in der Antwortvariablen darstellt, der durch die Prädiktorvariable erklärt werden kann.

Der Wert von R ² kann zwischen 0 und 1 variieren.

Da das R ² dieses speziellen Modells nahe bei 1 liegt, bedeutet dies, dass die Prädiktorvariable x den Wert der Antwortvariablen y gut vorhersagt.

Verwandt: Was ist ein guter R-Quadrat-Wert?

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige Vorgänge in Excel ausführen:

So verwenden Sie DEVSQ in Excel
So verwenden Sie SUMSQ in Excel
So führen Sie eine nichtlineare Regression in Excel durch