Einführung in die logistische regression

Wenn wir die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer kontinuierlichen Antwortvariablen verstehen möchten, verwenden wir häufig die lineare Regression .

Wenn die Antwortvariable jedoch kategorisch ist, können wir die logistische Regression verwenden.

Die logistische Regression ist eine Art Klassifizierungsalgorithmus , da sie versucht, Beobachtungen in einem Datensatz in verschiedene Kategorien zu „klassifizieren“.

Hier sind einige Beispiele für die Verwendung der logistischen Regression:

• Wir möchten anhand der Kreditwürdigkeit und des Bankguthabens vorhersagen, ob ein bestimmter Kunde mit einem Kredit in Zahlungsverzug gerät. (Antwortvariable = „Standard“ oder „Kein Standard“)
• Wir möchten die durchschnittlichen Rebounds pro Spiel und die durchschnittlichen Punkte pro Spiel verwenden, um vorherzusagen, ob ein bestimmter Basketballspieler in die NBA gedraftet wird oder nicht (Antwortvariable = „Drafted“ oder „Undrafted“).
• Wir möchten anhand der Quadratmeterzahl und der Anzahl der Badezimmer vorhersagen, ob ein Haus in einer bestimmten Stadt zu einem Verkaufspreis von 200.000 US-Dollar oder mehr angeboten wird. (Antwortvariable = „Ja“ oder „Nein“)

Beachten Sie, dass die Antwortvariable in jedem dieser Beispiele nur einen von zwei Werten annehmen kann. Vergleichen Sie dies mit der linearen Regression, bei der die Antwortvariable einen kontinuierlichen Wert annimmt.

Die logistische Regressionsgleichung

Die logistische Regression verwendet eine Methode, die als Maximum-Likelihood-Schätzung bekannt ist (auf die Details wird hier nicht eingegangen), um eine Gleichung der folgenden Form zu finden:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Gold:

• X _j : die j ^-te Vorhersagevariable
• β _j : Schätzung des Koeffizienten für die j ^-te Vorhersagevariable

Die Formel auf der rechten Seite der Gleichung sagt die logarithmische Wahrscheinlichkeit voraus, dass die Antwortvariable den Wert 1 annimmt.

Wenn wir also ein logistisches Regressionsmodell anpassen, können wir die folgende Gleichung verwenden, um die Wahrscheinlichkeit zu berechnen, dass eine bestimmte Beobachtung den Wert 1 annimmt:

p(X) = e ^{β ₀ + β _{1 X 1 + β 2 X 2 + … + β p}}

Anschließend verwenden wir einen bestimmten Wahrscheinlichkeitsschwellenwert, um die Beobachtung als 1 oder 0 zu klassifizieren.

Beispielsweise könnten wir sagen, dass Beobachtungen mit einer Wahrscheinlichkeit größer oder gleich 0,5 als „1“ und alle anderen Beobachtungen als „0“ klassifiziert werden.

Wie ist das Ergebnis der logistischen Regression zu interpretieren?

Angenommen, wir verwenden ein logistisches Regressionsmodell, um anhand seiner durchschnittlichen Rebounds pro Spiel und seiner durchschnittlichen Punkte pro Spiel vorherzusagen, ob ein bestimmter Basketballspieler in die NBA gedraftet wird oder nicht.

Hier ist das Ergebnis des logistischen Regressionsmodells:

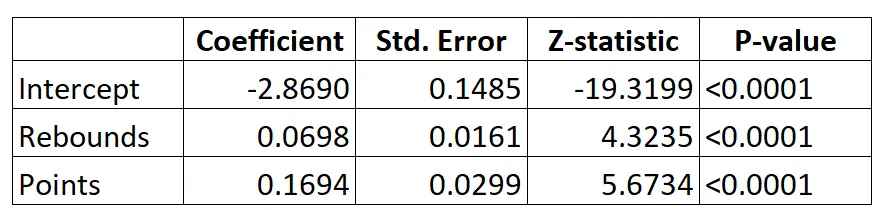
Mithilfe der Koeffizienten können wir anhand der durchschnittlichen Rebounds und Punkte pro Spiel die Wahrscheinlichkeit berechnen, dass ein bestimmter Spieler in die NBA gedraftet wird, und zwar mithilfe der folgenden Formel:

P(Entwurf) = e ^{-2,8690 + 0,0698*(rebs) + 0,1694*(punkte)} / (1+e ^{-2,8690 + 0,0698*(rebs) + 0,1694*(punkte) ) )}

Nehmen wir zum Beispiel an, dass ein bestimmter Spieler durchschnittlich 8 Rebounds pro Spiel und 15 Punkte pro Spiel erzielt. Dem Modell zufolge liegt die Wahrscheinlichkeit, dass dieser Spieler in die NBA gedraftet wird, bei 0,557 .

P(Geschrieben) = e ^{-2,8690 + 0,0698*(8) + 0,1694*(15)} / (1+e ^{-2,8690 + 0,0698*(8) + 0,1694*(15)} ) = 0,557

Da diese Wahrscheinlichkeit größer als 0,5 ist, gehen wir davon aus, dass dieser Spieler gedraftet wird.

Vergleichen Sie das mit einem Spieler, der im Durchschnitt nur 3 Rebounds und 7 Punkte pro Spiel erzielt. Die Wahrscheinlichkeit, dass dieser Spieler in die NBA gedraftet wird, beträgt 0,186 .

P(Geschrieben) = e ^{-2,8690 + 0,0698*(3) + 0,1694*(7)} / (1+e ^{-2,8690 + 0,0698*(3) + 0,1694*(7)} ) = 0,186

Da diese Wahrscheinlichkeit kleiner als 0,5 ist, gehen wir davon aus, dass dieser Spieler nicht gedraftet wird.

Annahmen zur logistischen Regression

Die logistische Regression verwendet die folgenden Annahmen:

1. Die Antwortvariable ist binär. Es wird davon ausgegangen, dass die Antwortvariable nur zwei mögliche Ergebnisse annehmen kann.

2. Beobachtungen sind unabhängig. Es wird davon ausgegangen, dass die Beobachtungen im Datensatz unabhängig voneinander sind. Das heißt, Beobachtungen sollten nicht aus wiederholten Messungen derselben Person stammen oder in irgendeiner Weise miteinander in Zusammenhang stehen.

3. Es besteht keine ernsthafte Multikollinearität zwischen den Prädiktorvariablen . Es wird davon ausgegangen, dass keine der Prädiktorvariablen stark miteinander korreliert ist.

4. Es gibt keine extremen Ausreißer. Es wird davon ausgegangen, dass der Datensatz keine extremen Ausreißer oder einflussreichen Beobachtungen enthält.

5. Es besteht eine lineare Beziehung zwischen den Prädiktorvariablen und dem Logit der Antwortvariablen . Diese Hypothese kann mit einem Box-Tidwell-Test überprüft werden.

6. Die Stichprobengröße ist groß genug. Normalerweise sollten Sie für jede erklärende Variable mindestens 10 Fälle mit dem seltensten Ergebnis haben. Wenn Sie beispielsweise drei erklärende Variablen haben und die erwartete Wahrscheinlichkeit des seltensten Ergebnisses 0,20 beträgt, sollten Sie eine Stichprobengröße von mindestens (10*3) / 0,20 = 150 haben.

In diesem Artikel erfahren Sie ausführlich, wie Sie diese Annahmen überprüfen können.