Logistische regression vs. lineare regression: die hauptunterschiede

Zwei der am häufigsten verwendeten Regressionsmodelle sind die lineare Regression und die logistische Regression .

Beide Arten von Regressionsmodellen werden verwendet, um die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen zu quantifizieren. Es gibt jedoch einige wesentliche Unterschiede zwischen den beiden Modellen:

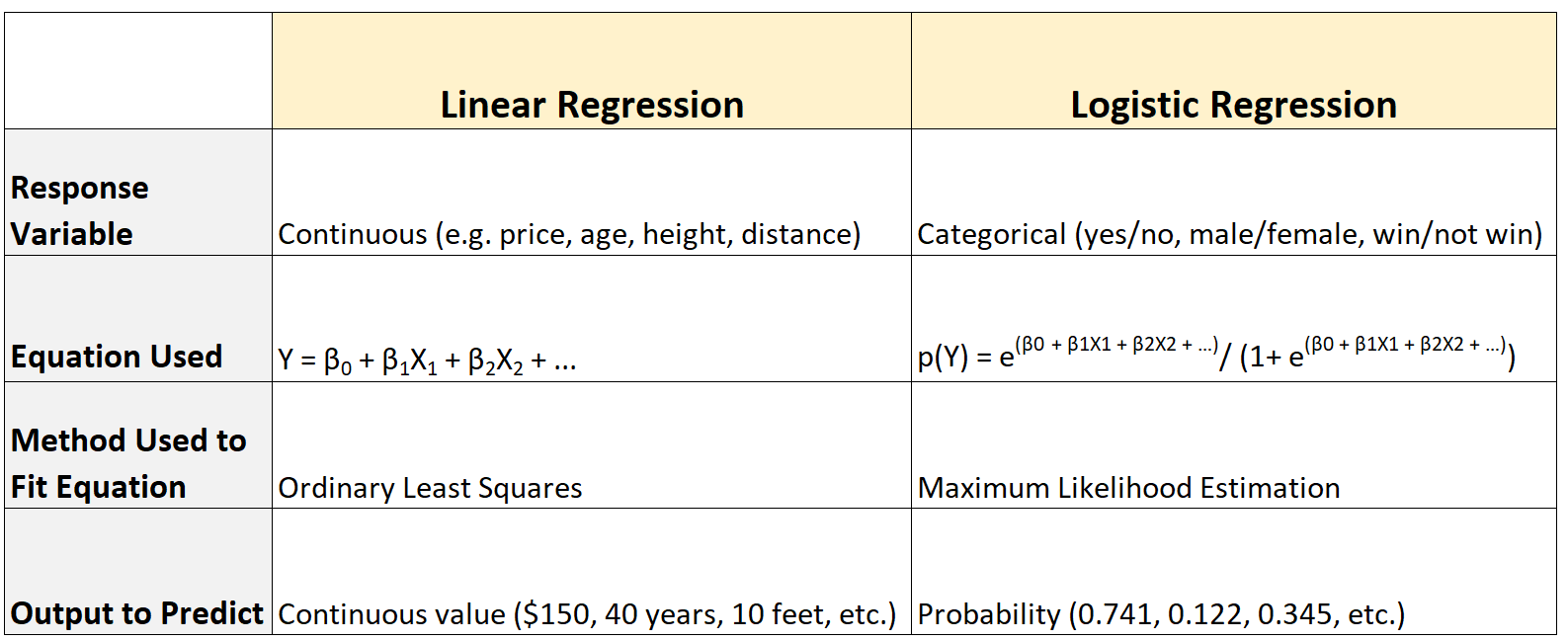
Hier ist eine Zusammenfassung der Unterschiede:

Unterschied Nr. 1: Antwortvariablentyp

Ein lineares Regressionsmodell wird verwendet, wenn die Antwortvariable einen kontinuierlichen Wert annimmt, sodass:

• Preis
• Höhe
• Alter
• Distanz

Umgekehrt wird ein logistisches Regressionsmodell verwendet, wenn die Antwortvariable einen kategorialen Wert annimmt, wie zum Beispiel:

• ja oder nein
• Männlich oder weiblich
• Gewinnen oder nicht gewinnen

Unterschied Nr. 2: verwendete Gleichung

Die lineare Regression verwendet die folgende Gleichung, um die Beziehung zwischen der/den Prädiktorvariablen und der Antwortvariablen zusammenzufassen:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Gold:

• Y: die Antwortvariable
• X _j : die j ^-te Vorhersagevariable
• β _j : Die durchschnittliche Auswirkung einer Erhöhung von X _j um eine Einheit auf Y, wobei alle anderen Prädiktoren unverändert bleiben

Umgekehrt verwendet die logistische Regression die folgende Gleichung:

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Diese Gleichung wird verwendet, um die Wahrscheinlichkeit vorherzusagen, dass eine einzelne Beobachtung in eine bestimmte Kategorie fällt.

Unterschied Nr. 3: Methode zur Anpassung der Gleichung

Die lineare Regression verwendet eine Methode, die als gewöhnliche kleinste Quadrate bekannt ist, um die am besten passende Regressionsgleichung zu finden.

Umgekehrt verwendet die logistische Regression eine Methode namens Maximum-Likelihood-Schätzung , um die am besten passende Regressionsgleichung zu finden.

Unterschied Nr. 4: Die Ausgabe muss vorhergesagt werden

Die lineare Regression sagt einen kontinuierlichen Wert als Ausgabe voraus. Zum Beispiel:

• Preis (150 $, 199 $, 400 $ usw.)
• Höhe (14 Zoll, 2 Fuß, 94,32 Zentimeter usw.)
• Alter (2 Monate, 6 Jahre, 41,5 Jahre usw.)
• Entfernung (1,23 Meilen, 4,5 Kilometer usw.)

Umgekehrt sagt die logistische Regression Wahrscheinlichkeiten als Ergebnis voraus. Zum Beispiel:

• 40,3 % Chance auf Aufnahme an einer Universität.
• 93,2 % Chance, ein Spiel zu gewinnen.
• 34,2 % Chance, dass ein Gesetz verabschiedet wird.

Wann sollte eine logistische oder lineare Regression verwendet werden?

Die folgenden Übungsaufgaben können Ihnen helfen, besser zu verstehen, wann Sie die logistische Regression oder die lineare Regression verwenden sollten.

Problem Nr. 1: Jahreseinkommen

Angenommen, ein Ökonom möchte Prädiktorvariablen (1) wöchentliche Arbeitsstunden und (2) Bildungsjahre verwenden, um das Jahreseinkommen von Einzelpersonen vorherzusagen.

In diesem Szenario würde er die lineare Regression verwenden, da die Antwortvariable (Jahreseinkommen) kontinuierlich ist.

Problem Nr. 2: Hochschulakzeptanz

Angenommen, ein Hochschulzulassungsbeamter möchte die Prädiktorvariablen (1) GPA und (2) ACT-Score verwenden, um die Wahrscheinlichkeit vorherzusagen, mit der ein Student an einer bestimmten Universität angenommen wird.

In diesem Szenario würde sie die logistische Regression verwenden, da die Antwortvariable kategorisch ist und nur zwei Werte annehmen kann: akzeptiert oder nicht akzeptiert.

Problem Nr. 3: Immobilienpreise

Angenommen, ein Immobilienmakler möchte die Prädiktorvariablen (1) Quadratmeterzahl, (2) Anzahl der Schlafzimmer und (3) Anzahl der Badezimmer verwenden, um die Verkaufspreise von Häusern vorherzusagen.

In diesem Szenario würde sie die lineare Regression verwenden, da die Antwortvariable (Preis) kontinuierlich ist.

Problem Nr. 4: Spam-Erkennung

Angenommen, ein Computerprogrammierer möchte die Prädiktorvariablen (1) Wortanzahl und (2) Herkunftsland verwenden, um die Wahrscheinlichkeit vorherzusagen, dass es sich bei einer bestimmten E-Mail um Spam handelt.

In diesem Szenario würde die logistische Regression verwendet, da die Antwortvariable kategorisch ist und nur zwei Werte annehmen kann: Spam oder kein Spam.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten weitere Details zur linearen Regression:

• Einführung in die einfache lineare Regression
• Einführung in die multiple lineare Regression
• 4 Beispiele für die Verwendung der linearen Regression im wirklichen Leben

Die folgenden Tutorials bieten weitere Details zur logistischen Regression:

• Einführung in die logistische Regression
• 4 Beispiele für die Verwendung der logistischen Regression im wirklichen Leben