Lorenzkurve

In diesem Artikel wird erklärt, was die Lorenz-Kurve ist und wofür sie verwendet wird. Sie erfahren, wie Sie die Lorenzkurve einer Grundgesamtheit erstellen und können außerdem die Lösung der Aufgabe Schritt für Schritt verfolgen. Abschließend werden die Eigenschaften der Lorenzkurve und der Zusammenhang mit dem Gini-Index vorgestellt.

Was ist die Lorenzkurve?

Die Lorenz-Kurve ist die grafische Darstellung der wirtschaftlichen Ungleichheiten der Bevölkerung eines Territoriums. Mit anderen Worten: Die Lorenz-Kurve ist eine Kurve, die es uns ermöglicht, Ungleichheiten in der Einkommensverteilung über ein Gebiet zu analysieren.

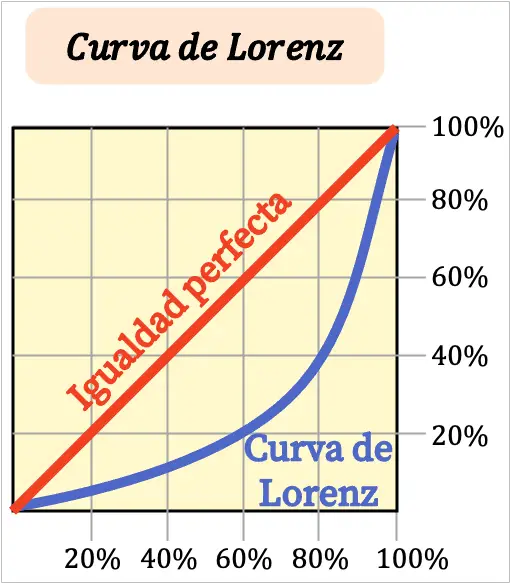
Je gerader die Lorenzkurve, desto egalitärer ist das Einkommen des Territoriums. Andererseits ist die Einkommensverteilung umso ungleicher, je stärker die Lorenzkurve verläuft.

Typischerweise werden die Achsen der Lorenz-Kurve als Prozentsätze ausgedrückt. Die X-Achse des Diagramms stellt den Bevölkerungsanteil dar, die Y-Achse dagegen den Einkommensanteil.

Die Lorenz-Kurve wurde 1905 von Max Otto Lorenz, einem sehr wichtigen amerikanischen Ökonomen des 20. Jahrhunderts, erfunden.

So berechnen Sie die Lorenzkurve

Sobald wir die Definition der Lorenz-Kurve kennen, werden wir sehen, wie diese statistische Kurve berechnet wird. Es ist zu beachten, dass es eine Formel zur Definition der Lorenzkurve gibt, diese in der Praxis jedoch im Allgemeinen nicht verwendet wird. Deshalb werden wir ein Beispiel Schritt für Schritt lösen, damit Sie sehen können, wie es gemacht wird.

• Stellt die Lorenz-Kurve der Bevölkerung dar, deren Einkommen in der folgenden Tabelle dargestellt ist:

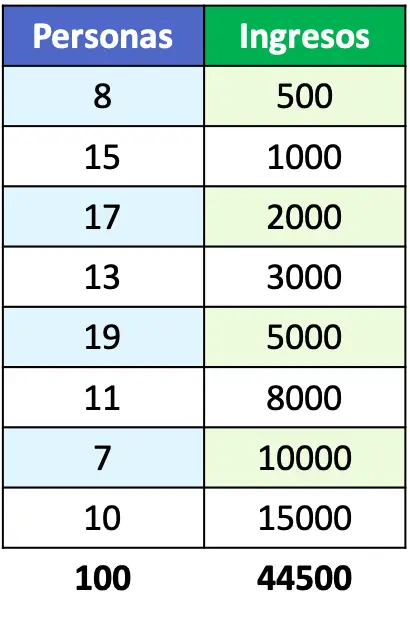
Wenn uns die Problemstellung das Beispiel einer Lorenzkurvenfunktion geben würde, könnten wir die Funktion direkt in einem Diagramm darstellen. Aber in diesem Fall geben sie uns nur das Bevölkerungseinkommen an, also müssen wir den Prozentsatz jeder Personengruppe berechnen.

Um also die Prozentsätze der Personenzahl und des Einkommens zu bestimmen, müssen wir der Tabelle für die Bevölkerungsvariable zwei Spalten hinzufügen:

• Eine Spalte mit der akkumulierten absoluten Häufigkeit (F _i ).
• Eine zweite Spalte, die dem kumulativen Prozentsatz entspricht, der berechnet wird, indem die kumulative absolute Häufigkeit durch die Gesamtzahl der Personen dividiert wird.

Und andererseits müssen wir drei Spalten für die Einkommensvariable hinzufügen:

• Spalte, in der das Gesamteinkommen berechnet wird, das dem Produkt aus der Anzahl der Personen und dem Einkommen entspricht, das jede Person erhält.
• Eine Sekunde mit der akkumulierten absoluten Häufigkeit (F _i ) des Gesamteinkommens.
• Eine dritte Spalte enthält den kumulierten Prozentsatz, der durch Division der vorherigen Spalte durch das Gesamteinkommen der Bevölkerung ermittelt wird.

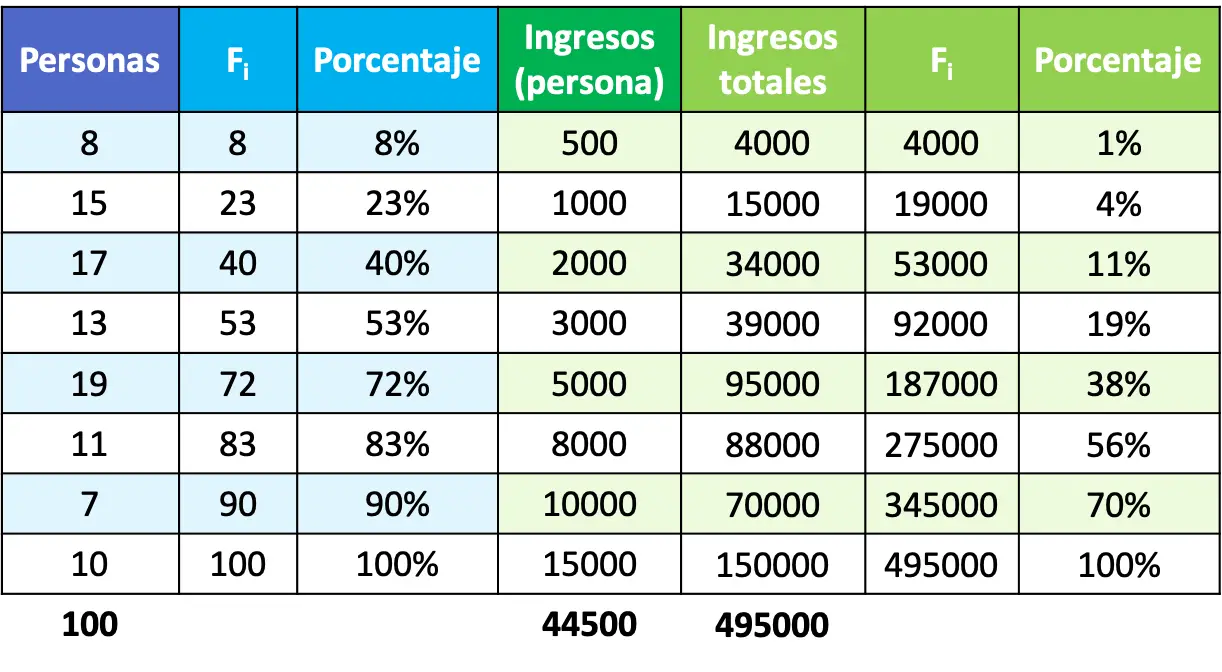
Nachdem wir nun die Prozentsätze berechnet haben, müssen wir nur noch die Punkte in ein Diagramm eintragen und sie zur Lorenzkurve zusammenfügen. Denken Sie daran, dass die X-Achse den Prozentsatz der Bevölkerung und die Y-Achse den Prozentsatz des Einkommens darstellt.

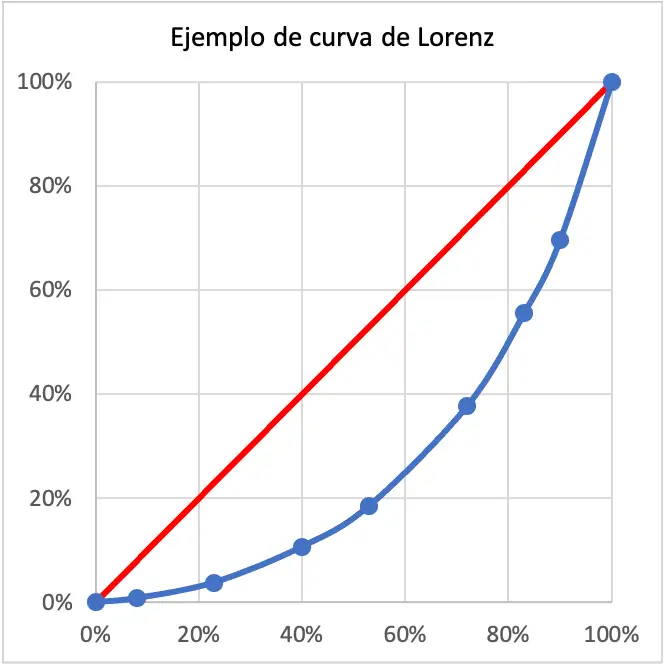
In diesem Fall ist das Einkommen der untersuchten Bevölkerung sehr ungleich, da die Lorenz-Kurve sehr breit ist. Tatsächlich ist die Lorenz-Kurve sehr weit von der roten Linie entfernt, die perfekte Gleichheit darstellt.

Interpretation der Lorenzkurve

In diesem Abschnitt wird erläutert, wie die Lorenz-Kurve einer Grundgesamtheit interpretiert wird, denn Sie müssen nicht nur wissen, wie man sie grafisch darstellt, sondern auch verstehen, was sie bedeutet.

Die Lorenz-Kurve gibt an, welcher Prozentsatz der Bevölkerung einen Prozentsatz des Gesamteinkommens eines Territoriums besitzt. Im oben gezeigten Beispiel der Lorenz-Kurve verfügen beispielsweise 40 % der Bevölkerung über ein Einkommen, das 11 % des gesamten Bevölkerungseinkommens ausmacht. Es handelt sich also um ein sehr unebenes Gebiet.

Somit stellt die Lorenz-Kurve visuell die Einkommensgleichheit oder -ungleichheit zwischen den Einwohnern eines Landes oder Territoriums dar . Je weiter wir uns von der Linie der vollkommenen Gleichheit entfernen, desto mehr bedeutet dies, dass das Einkommen der Bevölkerung ungleicher ist. Je näher die Lorenz-Kurve andererseits nach rechts rückt, desto mehr impliziert dies, dass das Einkommen der Bevölkerung gerechter verteilt ist.

Wenn außerdem eine Lorenz-Kurve im gesamten Diagramm über einer anderen Lorenz-Kurve liegt, bedeutet dies, dass das Einkommen der ersten Bevölkerung gleicher ist als das der zweiten.

Lorenz-Kurve und Gini-Koeffizient

Wie im gesamten Artikel erläutert, zeigt die Lorenz-Kurve grafisch, wie das Einkommen eines Territoriums verteilt ist und wie ungleich ein Territorium ist.

Andererseits gibt der Gini-Koeffizient, auch Gini-Index genannt, numerisch die wirtschaftliche Ungleichheit eines Territoriums an.

Die Lorenz-Kurve und der Gini-Koeffizient sind daher miteinander verknüpft. Tatsächlich kann der Gini-Koeffizient eines Landes aus seiner Lorenzkurve berechnet werden. Im folgenden Artikel können Sie sehen, wie das geht:

Eigenschaften der Lorenzkurve

Die Lorenz-Kurve hat folgende Eigenschaften:

• Die Lorenzkurve beginnt immer beim Punkt (0,0) und endet bei (100,100).
• Die Lorenz-Kurve ist undefiniert, wenn der Stichprobenmittelwert Null ist.
• Die Lorenz-Kurve kann in der Grafik nicht oberhalb der Linie vollkommener Gleichheit erscheinen.
• Unter der Annahme, dass das Einkommen nicht negativ sein kann, steigt die Lorenz-Kurve immer an.