Was wird durch varianz erklärt? (definition & #038; beispiel)

Die erklärte Varianz (manchmal auch „erklärte Variation“ genannt) bezieht sich auf die Varianz der Antwortvariablen in einem Modell, die durch die Prädiktorvariablen des Modells erklärt werden kann.

Je höher die erklärte Varianz eines Modells ist, desto mehr Variationen in den Daten kann das Modell erklären.

Die erklärte Varianz erscheint in den Ergebnissen zweier unterschiedlicher statistischer Modelle:

1. ANOVA: Wird verwendet, um die Mittelwerte von drei oder mehr unabhängigen Gruppen zu vergleichen.

2. Regression: Wird zur Quantifizierung der Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen verwendet.

Die folgenden Beispiele zeigen, wie die Restvarianz bei jeder dieser Methoden interpretiert wird.

Hinweis : Das Gegenteil der erklärten Varianz wird Restvarianz genannt.

Varianz erklärt in ANOVA-Modellen

Jedes Mal, wenn wir ein ANOVA-Modell („Varianzanalyse“) anpassen, erhalten wir eine ANOVA-Tabelle, die wie folgt aussieht:

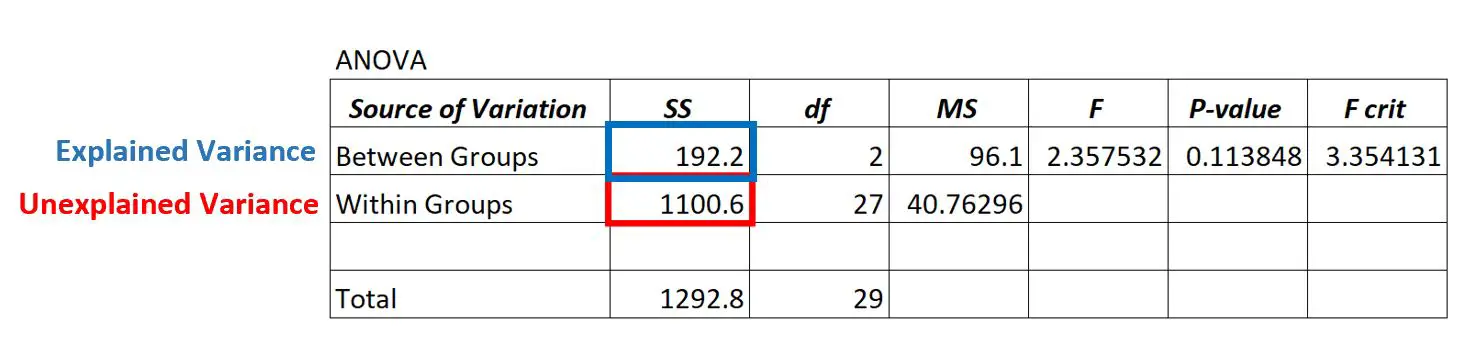
Die erklärte Varianz finden Sie in der SS-Spalte („Quadratsumme“) für die Variation zwischen Gruppen .

Im obigen ANOVA-Modell sehen wir, dass die erklärte Varianz 192,2 beträgt.

Um festzustellen, ob diese erklärte Varianz „hoch“ ist, können wir die mittlere Summe der Quadrate innerhalb von Gruppen und die mittlere Summe der Quadrate zwischen Gruppen berechnen und das Verhältnis zwischen beiden ermitteln, das den Gesamt-F-Wert in der ANOVA-Tabelle ergibt.

• F = MS _{kommt herein} / MS _rein
• F = 96,1 / 40,76296
• F = 2,357

Der F-Wert in der ANOVA-Tabelle oben beträgt 2,357 und der entsprechende p-Wert beträgt 0,113848.

Da dieser p-Wert nicht kleiner als α = 0,05 ist, haben wir keine ausreichenden Beweise, um die Nullhypothese der ANOVA abzulehnen.

Das bedeutet, dass uns keine ausreichenden Beweise dafür vorliegen, dass der mittlere Unterschied zwischen den Gruppen, die wir vergleichen, signifikant unterschiedlich ist.

Dies zeigt uns, dass die erklärte Varianz im ANOVA-Modell im Vergleich zur ungeklärten Varianz gering ist.

Varianz erklärt in Regressionsmodellen

In einem Regressionsmodell wird die erklärte Varianz als R-Quadrat zusammengefasst, oft ^{als R2} geschrieben.

Dieser Wert stellt den Anteil der Varianz in der Antwortvariablen dar, der durch die Prädiktorvariablen im Modell erklärt werden kann.

Der Wert von R im Quadrat kann zwischen 0 und Folgendem liegen:

• Ein Wert von 0 gibt an, dass die Antwortvariable überhaupt nicht durch die Prädiktorvariablen erklärt werden kann.
• Ein Wert von 1 gibt an, dass die Antwortvariable perfekt und fehlerfrei durch die Prädiktorvariablen erklärt werden kann.

Wenn wir ein Regressionsmodell anpassen, erhalten wir normalerweise ein Ergebnis, das wie folgt aussieht:

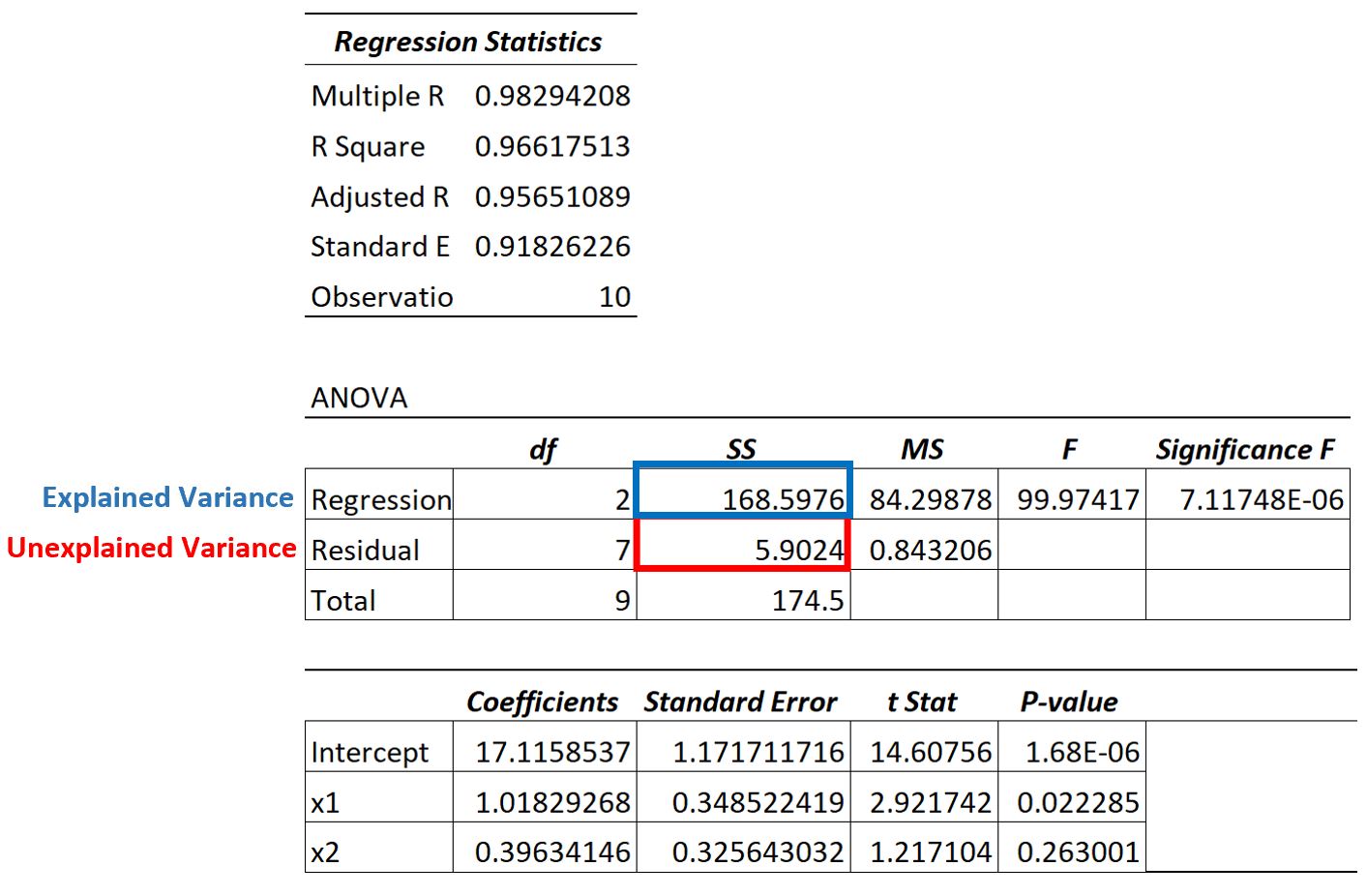
Wir können sehen, dass die erklärte Varianz 168,5976 und die Gesamtvarianz 174,5 beträgt.

Mit diesen Werten können wir den R-Quadrat-Wert für dieses Regressionsmodell wie folgt berechnen:

• R im Quadrat: Regressions-SS / Gesamt-SS
• R im Quadrat: 168,5976 / 174,5
• R im Quadrat: 0,966

Da der R-Quadrat-Wert dieses Modells nahe bei 1 liegt, bedeutet dies, dass die im Modell erklärte Varianz extrem hoch ist.

Mit anderen Worten: Das Modell ist in der Lage, mithilfe der Prädiktorvariablen die Variation in der Antwortvariablen gut zu erklären.

Verwandt: Was ist ein guter R-Quadrat-Wert?