Mae vs. rmse: welche metrik sollten sie verwenden?

Regressionsmodelle werden verwendet, um die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen zu quantifizieren.

Wann immer wir ein Regressionsmodell anpassen, möchten wir verstehen, wie gut das Modell die Werte der Prädiktorvariablen verwenden kann, um den Wert der Antwortvariablen vorherzusagen.

Zwei Metriken, die wir häufig verwenden, um zu quantifizieren, wie gut ein Modell zu einem Datensatz passt, sind der mittlere absolute Fehler (MAE) und der mittlere quadratische Fehler (RMSE), die wie folgt berechnet werden:

MAE : Eine Metrik, die uns die durchschnittliche absolute Differenz zwischen vorhergesagten Werten und tatsächlichen Werten in einem Datensatz angibt. Je niedriger der MAE, desto besser passt ein Modell zu einem Datensatz.

MAE = 1/n * Σ|y _i – ŷ _i |

Gold:

• Σ ist ein Symbol, das „Summe“ bedeutet
• y _i ist der beobachtete Wert für die ^i-te Beobachtung
• ŷ _i ist der vorhergesagte Wert für die i- ^te Beobachtung
• n ist die Stichprobengröße

RMSE : Eine Metrik, die uns die Quadratwurzel der quadratischen Mittelwertdifferenz zwischen den vorhergesagten Werten und den tatsächlichen Werten in einem Datensatz angibt. Je niedriger der RMSE, desto besser passt ein Modell zu einem Datensatz.

Es wird wie folgt berechnet:

RMSE = √ Σ(y _i – ŷ _i ) ² / n

Gold:

• Σ ist ein Symbol, das „Summe“ bedeutet
• ŷ _i ist der vorhergesagte Wert für die i- ^te Beobachtung
• y _i ist der beobachtete Wert für die ^i-te Beobachtung
• n ist die Stichprobengröße

Beispiel: Berechnung von RMSE und MAE

Angenommen, wir verwenden ein Regressionsmodell, um vorherzusagen, wie viele Punkte 10 Spieler in einem Basketballspiel erzielen werden.

Die folgende Tabelle zeigt die vom Modell vorhergesagten Punkte im Vergleich zu den tatsächlich von den Spielern erzielten Punkten:

Mit dem MAE-Rechner können wir berechnen, dass der MAE 3,2 beträgt.

Dies sagt uns, dass die durchschnittliche absolute Differenz zwischen den vom Modell vorhergesagten Werten und den tatsächlichen Werten 3,2 beträgt.

Mit dem RMSE-Rechner können wir berechnen, dass der RMSE gleich 4 ist.

Dies sagt uns, dass die Quadratwurzel der quadratischen Mittelwertdifferenzen zwischen den vorhergesagten und den tatsächlich erzielten Punkten 4 beträgt.

Beachten Sie, dass jede Metrik uns eine Vorstellung vom typischen Unterschied zwischen dem vom Modell vorhergesagten Wert und dem tatsächlichen Wert im Datensatz gibt, die Interpretation jeder Metrik jedoch etwas anders ist.

RMSE vs. MAE: Welche Metrik sollten Sie verwenden?

Wenn Sie Beobachtungen, die weiter vom Mittelwert entfernt sind, mehr Gewicht zuweisen möchten (d. h. wenn eine Abweichung von 20 mehr als doppelt so schlecht ist wie eine Abweichung von 10), ist es besser, den RMSE zur Fehlermessung zu verwenden, da dies beim RMSE der Fall ist empfindlicher gegenüber Beobachtungen, die weiter vom Mittelwert entfernt sind.

Wenn jedoch ein „Offset“ bei 20 doppelt so schlimm ist wie ein „Offset“ bei 10, dann ist es besser, den MAE zu verwenden.

Um dies zu veranschaulichen, nehmen wir an, dass wir einen Spieler haben, der in Bezug auf die Anzahl der erzielten Punkte ein klarer Ausreißer ist:

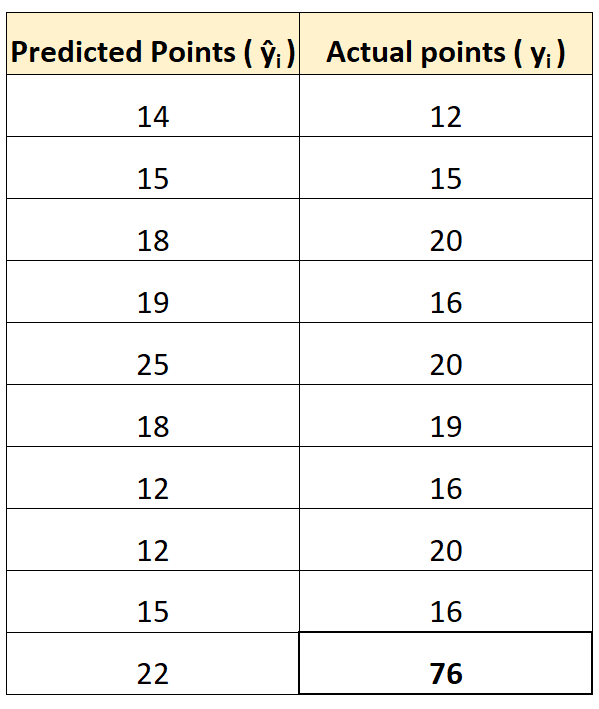
Mit den zuvor erwähnten Online-Rechnern können wir MAE und RMSE wie folgt berechnen:

• MAE : 8
• RMSE : 16,4356

Beachten Sie, dass der RMSE viel stärker ansteigt als der MAE.

Dies liegt daran, dass RMSE in seiner Formel quadratische Differenzen verwendet und die quadrierte Differenz zwischen dem beobachteten Wert von 76 und dem vorhergesagten Wert von 22 ziemlich groß ist. Dies führt zu einer deutlichen Erhöhung des RMSE-Wertes.

In der Praxis passen wir normalerweise mehrere Regressionsmodelle an einen Datensatz an und berechnen für jedes Modell nur eine dieser Metriken.

Wir könnten beispielsweise drei verschiedene Regressionsmodelle anpassen und den RMSE für jedes Modell berechnen. Wir würden dann das Modell mit dem niedrigsten RMSE-Wert als „bestes“ Modell auswählen, da es dasjenige ist, dessen Vorhersagen den tatsächlichen Werten im Datensatz am nächsten kommen.

Stellen Sie in jedem Fall sicher, dass Sie für jedes Modell die gleiche Metrik berechnen. Berechnen Sie beispielsweise nicht den MAE für ein Modell und den RMSE für ein anderes Modell und vergleichen Sie dann diese beiden Messungen.

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie man MAE mit unterschiedlicher Statistiksoftware berechnet:

So berechnen Sie den mittleren absoluten Fehler in Excel
So berechnen Sie den mittleren absoluten Fehler in R
So berechnen Sie den mittleren absoluten Fehler in Python

Die folgenden Tutorials erklären, wie man RMSE mit unterschiedlicher Statistiksoftware berechnet:

So berechnen Sie den mittleren quadratischen Fehler in Excel
So berechnen Sie den mittleren quadratischen Fehler in R
So berechnen Sie den mittleren quadratischen Fehler in Python