So führen sie einen lack-of-fit-test in r durch (schritt für schritt)

Mit einem Test auf fehlende Anpassung wird ermittelt, ob ein vollständiges Regressionsmodell eine deutlich bessere Anpassung an einen Datensatz bietet als eine reduzierte Version des Modells.

Angenommen, wir möchten die Anzahl der gelernten Stunden verwenden, um die Prüfungsergebnisse für Studenten einer bestimmten Hochschule vorherzusagen. Wir können uns entscheiden, die folgenden zwei Regressionsmodelle anzupassen:

Vollständiges Modell: Punktzahl = β ₀ + B ₁ (Stunden) + B ₂ (Stunden) ²

Reduziertes Modell: Punktzahl = β ₀ + B ₁ (Stunden)

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie in R einen Test auf mangelnde Anpassung durchführen, um festzustellen, ob das vollständige Modell eine deutlich bessere Anpassung bietet als das reduzierte Modell.

Schritt 1: Erstellen und visualisieren Sie einen Datensatz

Zuerst verwenden wir den folgenden Code, um einen Datensatz zu erstellen, der die Anzahl der gelernten Stunden und die erzielten Prüfungsergebnisse für 50 Studenten enthält:

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Als Nächstes erstellen wir ein Streudiagramm, um die Beziehung zwischen Stunden und Punktzahl zu visualisieren:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

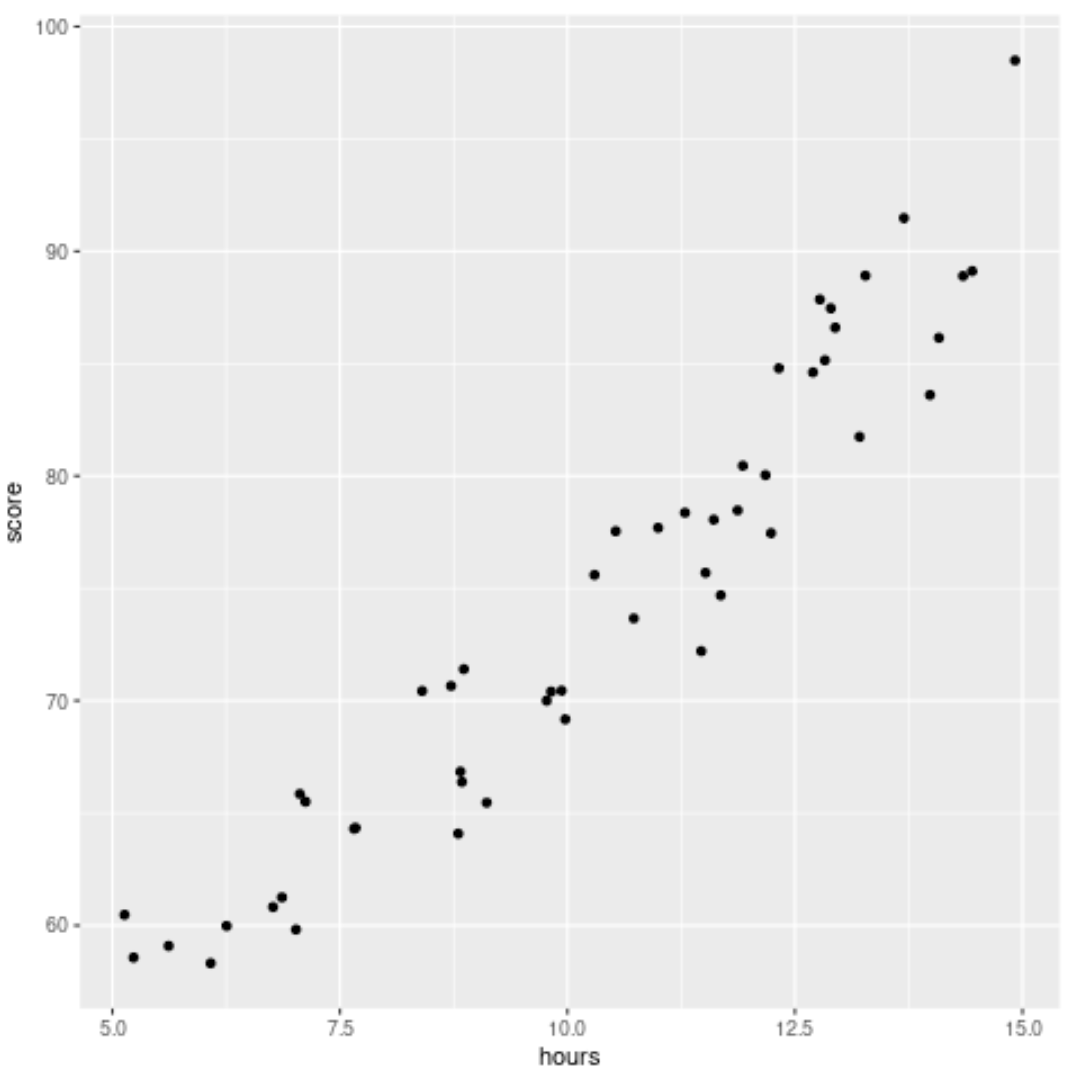
Schritt 2: Passen Sie zwei verschiedene Modelle an den Datensatz an

Als nächstes passen wir zwei verschiedene Regressionsmodelle an den Datensatz an:

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

Schritt 3: Führen Sie einen Dichtsitztest durch

Als nächstes verwenden wir den Befehl anova() , um einen Test auf fehlende Passung zwischen den beiden Modellen durchzuführen:

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Die F-Teststatistik beträgt 10,554 und der entsprechende p-Wert beträgt 0,002144 . Da dieser p-Wert kleiner als 0,05 ist, können wir die Nullhypothese des Tests ablehnen und daraus schließen, dass das vollständige Modell eine statistisch signifikant bessere Anpassung bietet als das reduzierte Modell.

Schritt 4: Visualisieren Sie das endgültige Modell

Schließlich können wir das endgültige Modell (das vollständige Modell) anhand des Originaldatensatzes visualisieren:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

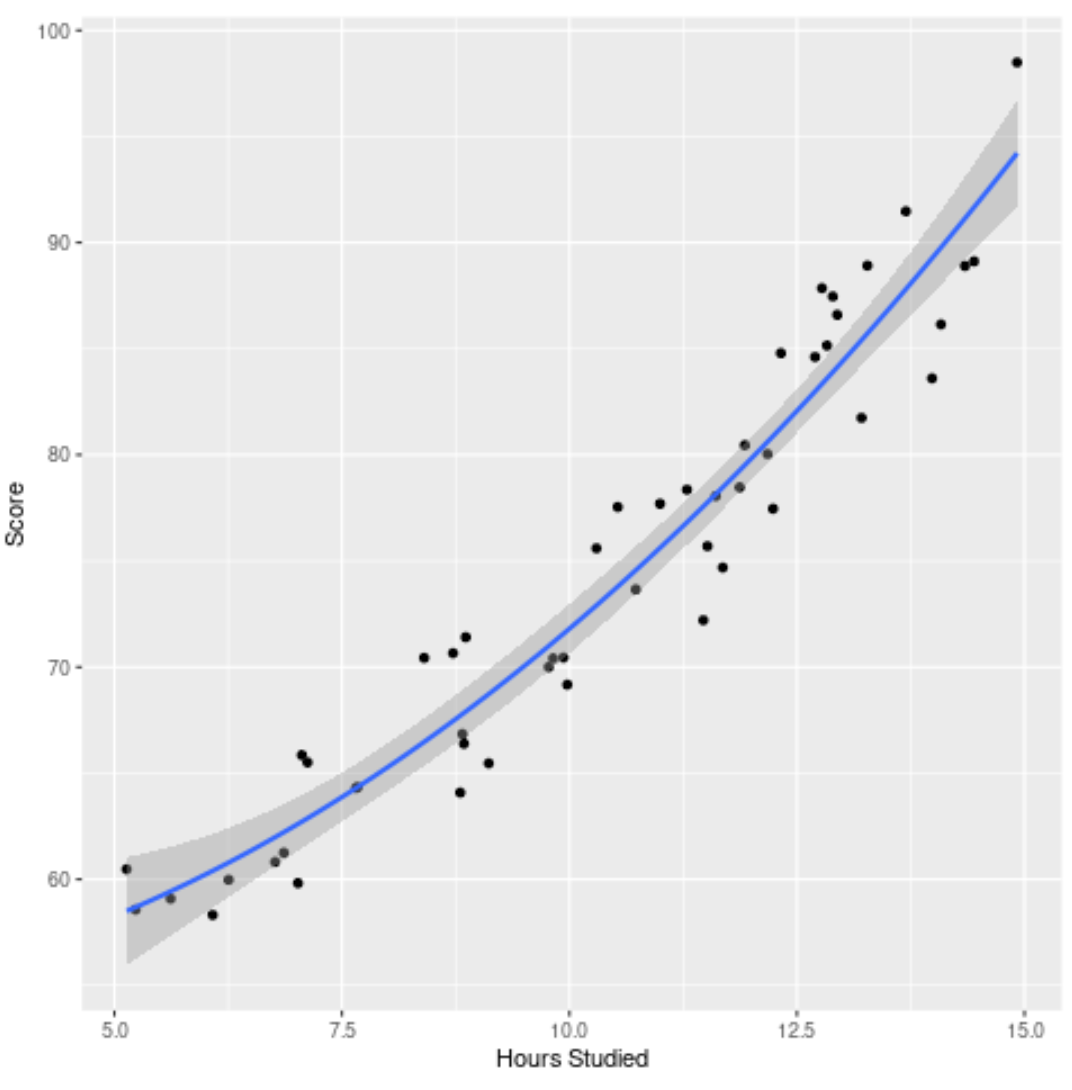
Wir können sehen, dass die Modellkurve recht gut zu den Daten passt.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine Polynomregression in R durch