So führen sie einen mann-kendall-trendtest in r durch

Mithilfe eines Mann-Kendall-Trendtests wird ermittelt, ob in Zeitreihendaten ein Trend vorliegt oder nicht. Hierbei handelt es sich um einen nichtparametrischen Test, d. h. es werden keine zugrunde liegenden Annahmen über die Normalität der Daten getroffen.

Die Testhypothesen lauten wie folgt:

H ₀ (Nullhypothese): In den Daten ist kein Trend vorhanden.

H _A (Alternativhypothese): In den Daten ist ein Trend vorhanden. (Dies könnte ein positiver oder negativer Trend sein)

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (übliche Werte sind 0,10, 0,05 und 0,01), dann gibt es statistisch signifikante Hinweise darauf, dass in den Daten der Zeitreihe ein Trend vorhanden ist.

In diesem Tutorial wird erläutert, wie ein Mann-Kendall-Trendtest in R durchgeführt wird.

Beispiel: Mann-Kendall-Trendtest in R

Um einen Mann-Kendall-Trendtest in R durchzuführen, verwenden wir die Funktion MannKendall() aus der Kendall- Bibliothek, die die folgende Syntax verwendet:

MannKendall(x)

Gold:

• x = ein Datenvektor, oft eine Zeitreihe

Um zu veranschaulichen, wie der Test durchgeführt wird, verwenden wir den integrierten PrecipGL- Datensatz der Kendall Library, der jährliche Niederschlagsinformationen für alle Großen Seen von 1900 bis 1986 enthält:

 #load Kendall library and PrecipGL dataset
library(Kendall)
data(PrecipGL)

#view dataset
PrecipGL

Time Series:
Start = 1900 
End = 1986 
Frequency = 1 
[1] 31.69 29.77 31.70 33.06 31.31 32.72 31.18 29.90 29.17 31.48 28.11 32.61
[13] 31.31 30.96 28.40 30.68 33.67 28.65 30.62 30.21 28.79 30.92 30.92 28.13
[25] 30.51 27.63 34.80 32.10 33.86 32.33 25.69 30.60 32.85 30.31 27.71 30.34
[37] 29.14 33.41 33.51 29.90 32.69 32.34 35.01 33.05 31.15 36.36 29.83 33.70
[49] 29.81 32.41 35.90 37.45 30.39 31.15 35.75 31.14 30.06 32.40 28.44 36.38
[61] 31.73 31.27 28.51 26.01 31.27 35.57 30.85 33.35 35.82 31.78 34.25 31.43
[73] 35.97 33.87 28.94 34.62 31.06 38.84 32.25 35.86 32.93 32.69 34.39 33.97
[85] 32.15 40.16 36.32
attr(,"title")
[1] Annual precipitation, 1900-1986, Entire Great Lakes

Um zu sehen, ob es einen Trend in den Daten gibt, können wir den Mann-Kendall-Trendtest durchführen:

 #Perform the Mann-Kendall Trend Test
MannKendall(PrecipGL)

tau = 0.265, 2-sided pvalue = 0.00029206

Die Teststatistik beträgt 0,265 und der entsprechende zweiseitige p-Wert beträgt 0,00029206 . Da dieser p-Wert kleiner als 0,05 ist, lehnen wir die Nullhypothese des Tests ab und kommen zu dem Schluss, dass in den Daten ein Trend vorliegt.

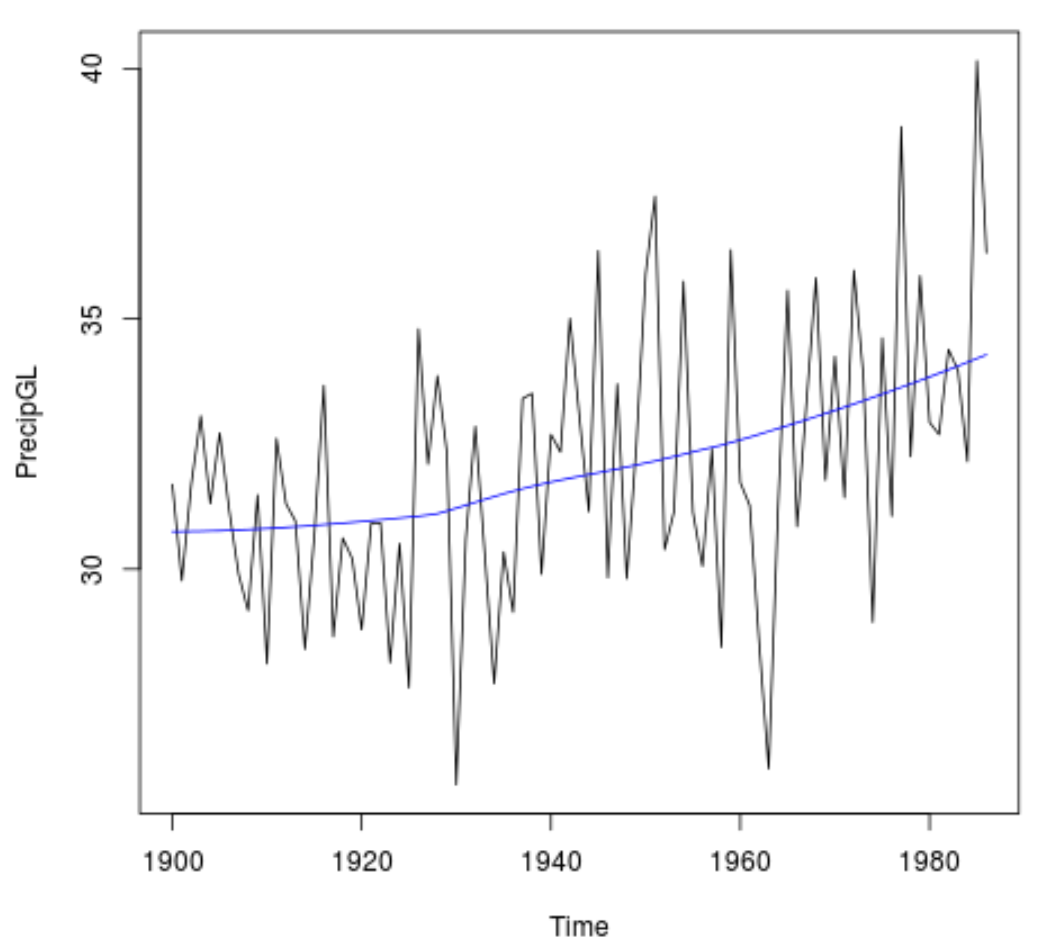
Um den Trend zu visualisieren, können wir ein Zeitdiagramm der jährlichen Niederschläge pro Jahr erstellen und eine glatte Linie hinzufügen, um den Trend darzustellen:

 #Plot the time series data
plot(PrecipGL)

#Add a smooth line to visualize the trend 
lines(lowess(time(PrecipGL),PrecipGL), col='blue')

Beachten Sie, dass wir mit dem Befehl SeasonalMannKendall(x) auch einen saisonbereinigten Mann-Kendall-Trendtest durchführen können, um jegliche Saisonalität in den Daten zu berücksichtigen:

 #Perform a seasonally-adjusted Mann-Kendall Trend Test
SeasonalMannKendall(PrecipGL)

tau = 0.265, 2-sided pvalue = 0.00028797

Die Teststatistik beträgt 0,265 und der entsprechende zweiseitige p-Wert beträgt 0,00028797 . Auch dieser p-Wert liegt unter 0,05, daher lehnen wir die Nullhypothese des Tests ab und kommen zu dem Schluss, dass in den Daten ein Trend vorliegt.