Der vollständige leitfaden: so überprüfen sie manova-annahmen

Eine MANOVA (multivariate Varianzanalyse) wird verwendet, um zu analysieren, wie sich eine oder mehrere Faktorvariablen auf mehrere Antwortvariablen auswirken.

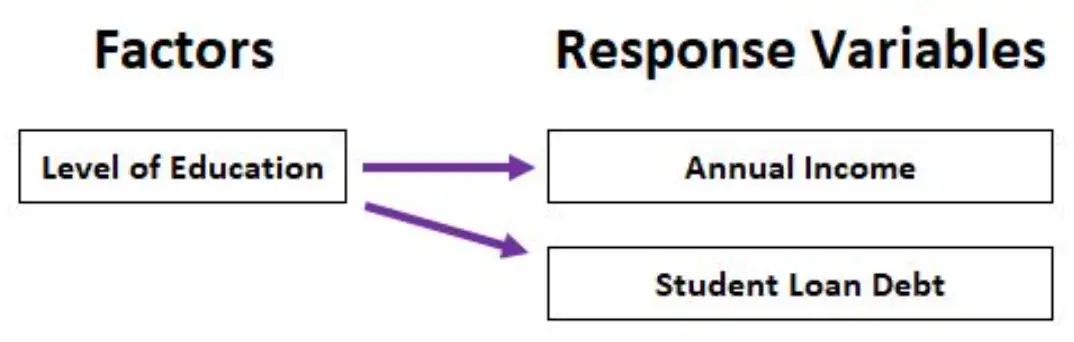
Beispielsweise könnten wir eine MANOVA verwenden, um zu analysieren, wie sich das Bildungsniveau (High-School-Abschluss, Associate-Abschluss, Bachelor-Abschluss, Master-Abschluss) sowohl auf das Jahreseinkommen als auch auf die gesamten Studienkreditschulden auswirkt.

Verwandt: Die Unterschiede zwischen ANOVA, ANCOVA, MANOVA und MANCOVA

Jedes Mal, wenn wir eine MANOVA durchführen, müssen wir überprüfen, ob die folgenden Annahmen erfüllt sind:

1. Multivariate Normalität – Die Antwortvariablen sind multivariat normalverteilt innerhalb jeder Gruppe von Faktorvariablen.

2. Unabhängigkeit – Jede Beobachtung wird zufällig und unabhängig aus der Grundgesamtheit ausgewählt.

3. Gleiche Varianz – Die Populationskovarianzmatrizen jeder Gruppe sind gleich.

4. Keine multivariaten Ausreißer – Es gibt keine extremen multivariaten Ausreißer.

In diesem Artikel erläutern wir jede Annahme und erläutern, wie Sie feststellen können, ob die Annahme erfüllt ist.

Annahme 1: Multivariate Normalität

Eine MANOVA geht davon aus, dass die Antwortvariablen innerhalb jeder Gruppe der Faktorvariablen multivariat normalverteilt sind.

Wenn es für jede Kombination aus Faktor und Antwortvariable mindestens 20 Beobachtungen gibt, können wir davon ausgehen, dass die Annahme der multivariaten Normalität erfüllt ist.

Wenn es weniger als 20 Beobachtungen für jede Kombination aus Faktor und Antwortvariable gibt, können wir eine Streudiagrammmatrix erstellen, um die Residuen zu visualisieren und visuell zu überprüfen, ob diese Annahme erfüllt ist.

Glücklicherweise ist bekannt, dass MANOVA robust gegenüber Abweichungen von der multivariaten Normalität ist, sodass kleine bis mittlere Abweichungen im Allgemeinen kein Problem darstellen.

Hypothese 2: Unabhängigkeit

Bei einer MANOVA wird davon ausgegangen, dass jede Beobachtung zufällig und unabhängig aus der Grundgesamtheit entnommen wird.

Solange eine Wahrscheinlichkeitsstichprobenmethode (jedes Mitglied einer Population hat die gleiche Wahrscheinlichkeit, in die Stichprobe aufgenommen zu werden) zum Sammeln der Daten verwendet wird, können wir davon ausgehen, dass jede Beobachtung zufällig und unabhängig ausgewählt wurde.

Beispiele für Wahrscheinlichkeitsstichprobenmethoden sind:

• Einfache Zufallsstichprobe
• Geschichtete Zufallsstichprobe
• Zufällige Cluster-Stichprobe
• Systematische Zufallsauswahl

Annahme 3: gleiche Varianz

Eine MANOVA geht davon aus, dass die Populationskovarianzmatrizen jeder Gruppe gleich sind.

Die gebräuchlichste Methode zum Testen dieser Hypothese ist die Verwendung des M-Tests von Box. Dieser Test ist bekanntermaßen recht streng, weshalb wir im Allgemeinen ein Signifikanzniveau von 0,001 verwenden, um zu bestimmen, ob die Kovarianzmatrizen der Population gleich sind oder nicht.

Wenn der p-Wert des M-Tests von Box größer als 0,001 ist, können wir davon ausgehen, dass diese Annahme erfüllt ist.

Glücklicherweise ist eine MANOVA tendenziell robust gegenüber Abweichungen von dieser Hypothese, selbst wenn der p-Wert des Tests weniger als 0,001 beträgt.

Damit ungleiche Kovarianzmatrizen ein Problem darstellen, müssen die Unterschiede zwischen den Kovarianzmatrizen ziemlich extrem sein.

Hypothese 4: keine multivariaten Ausreißer

Eine MANOVA geht davon aus, dass in den Daten keine extremen multivariaten Ausreißer vorhanden sind, die die Ergebnisse erheblich beeinflussen könnten.

Der gebräuchlichste Weg, diese Annahme zu überprüfen, besteht darin, für jede Beobachtung den Mahalanobis-Abstand zu berechnen, der den Abstand zwischen zwei Punkten in einem multivariaten Raum darstellt.

Wenn der entsprechende p-Wert für eine Mahalanobis-Distanz einer Beobachtung kleiner als 0,001 ist, erklären wir diese Beobachtung im Allgemeinen als extremen Ausreißer.

Sehen Sie sich die folgenden Tutorials an, um zu erfahren, wie Sie die Mahalanobis-Distanz in verschiedenen Statistikprogrammen berechnen:

• So berechnen Sie den Mahalanobis-Abstand in R
• So berechnen Sie die Mahalanobis-Distanz in SPSS
• So berechnen Sie die Mahalanobis-Distanz in Python

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie man eine MANOVA in verschiedenen Statistikprogrammen durchführt:

So führen Sie eine MANOVA in R durch
So führen Sie eine MANOVA in SPSS durch
So führen Sie eine MANOVA in Stata durch