So führen sie eine manova in stata durch

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob unterschiedliche Niveaus einer erklärenden Variablen zu statistisch unterschiedlichen Ergebnissen bei bestimmten Antwortvariablen führen.

Beispielsweise könnte es uns interessieren, ob drei Bildungsniveaus (Associate-Abschluss, Bachelor-Abschluss, Master-Abschluss) zu statistisch unterschiedlichen Jahresverdiensten führen. In diesem Fall haben wir eine erklärende Variable und eine Antwortvariable.

• Erklärende Variable: Bildungsniveau
• Antwortvariable: Jahreseinkommen

Eine MANOVA ist eine Erweiterung der einfaktoriellen ANOVA, in der es mehr als eine Antwortvariable gibt. Beispielsweise könnte es für uns von Interesse sein zu verstehen, ob das Bildungsniveau zu unterschiedlichen Jahreseinkommen und unterschiedlich hohen Studienschulden führt. In diesem Fall haben wir eine erklärende Variable und zwei Antwortvariablen:

• Erklärende Variable: Bildungsniveau
• Antwortvariablen: Jahreseinkommen, Studienschulden

Da wir mehr als eine Antwortvariable haben, wäre es in diesem Fall angemessen, eine MANOVA zu verwenden.

Als nächstes erklären wir, wie man eine MANOVA in Stata durchführt.

Beispiel: MANOVA in Stata

Um zu veranschaulichen, wie eine MANOVA in Stata durchgeführt wird, verwenden wir den folgenden Datensatz, der die folgenden drei Variablen für 24 Personen enthält:

• educ: Studienniveau (0 = Associate, 1 = Bachelor, 2 = Master)
• Einkommen: Jahreseinkommen
• Schulden: Gesamtschulden des Studiendarlehens

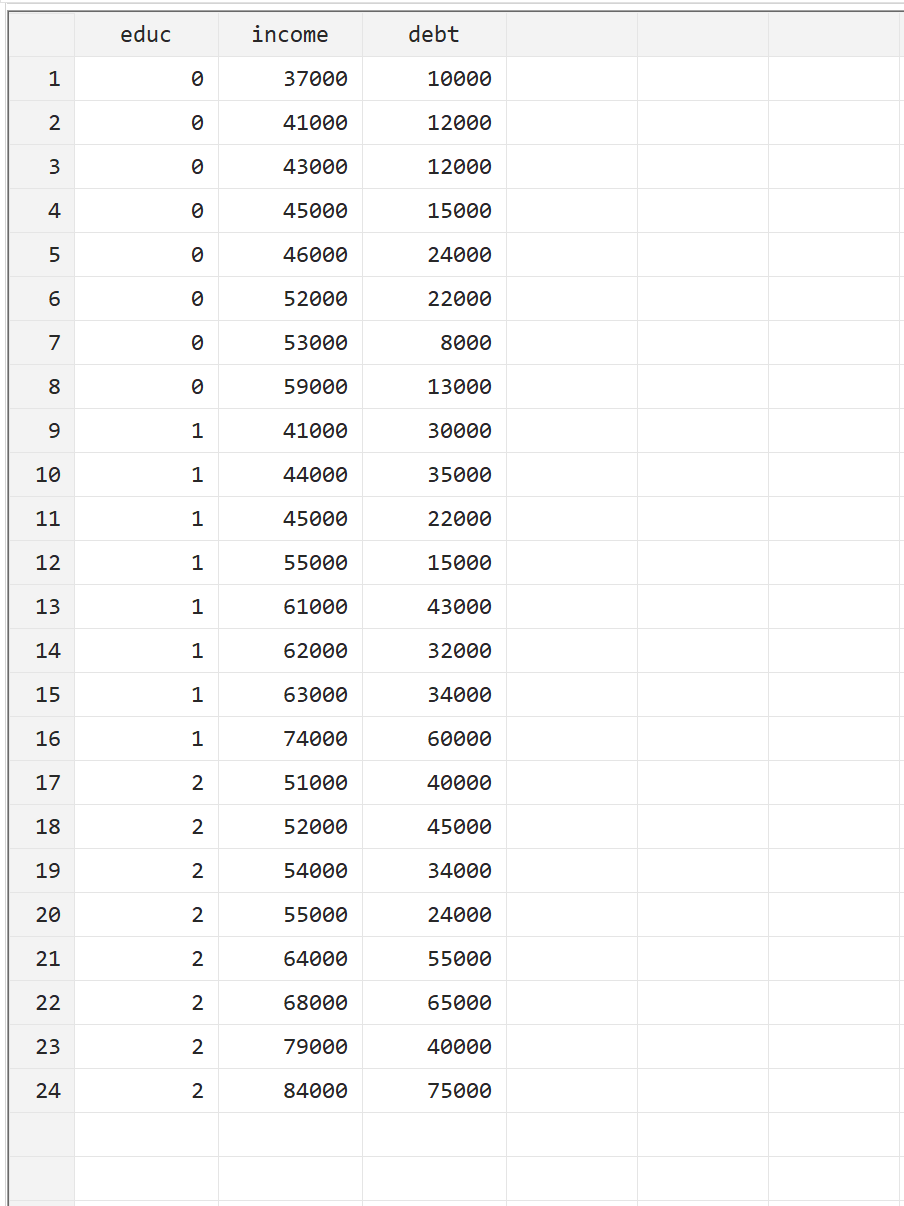
Sie können dieses Beispiel reproduzieren, indem Sie die Daten selbst manuell eingeben, indem Sie in der oberen Menüleiste zu Daten > Dateneditor > Dateneditor (Bearbeiten) navigieren.

Um die MANOVA unter Verwendung von Bildung als erklärender Variable und Einkommen und Schulden als Antwortvariablen durchzuführen, können wir den folgenden Befehl verwenden:

Einkommensschulden manova = educ

Stata erstellt vier einzigartige Teststatistiken zusammen mit den entsprechenden p-Werten:

Wilks‘ Lambda: F-Statistik = 5,02, P-Wert = 0,0023.

Pillai-Spur: F-Statistik = 4,07, P-Wert = 0,0071.

Lawley-Hotelling-Kurve: F-Statistik = 5,94, P-Wert = 0,0008.

Größte Roy-Wurzel: F-Statistik = 13,10, P-Wert = 0,0002.

Eine detaillierte Erklärung, wie die einzelnen Teststatistiken berechnet werden, finden Sie in diesem Artikel des Penn State Eberly College of Science.

Der p-Wert für jede Teststatistik liegt unter 0,05, sodass die Nullhypothese unabhängig davon, welche Sie verwenden, abgelehnt wird. Dies bedeutet, dass wir über genügend Beweise verfügen, um zu sagen, dass das Bildungsniveau statistisch signifikante Unterschiede im Jahreseinkommen und in der Gesamtverschuldung der Studierenden verursacht.

Hinweis zu p-Werten: Der Buchstabe neben dem p-Wert in der Ausgabetabelle gibt an, wie die F-Statistik berechnet wurde (e = genaue Berechnung, a = ungefähre Berechnung, u = Obergrenze).