So erstellen sie eine verwirrungsmatrix in r (schritt für schritt)

Die logistische Regression ist eine Art Regression, die wir verwenden können, wenn die Antwortvariable binär ist.

Eine gängige Methode zur Beurteilung der Qualität eines logistischen Regressionsmodells besteht darin, eine Verwirrungsmatrix zu erstellen, bei der es sich um eine 2 × 2-Tabelle handelt, die die vorhergesagten Werte des Modells im Vergleich zu den tatsächlichen Werten des Testdatensatzes zeigt.

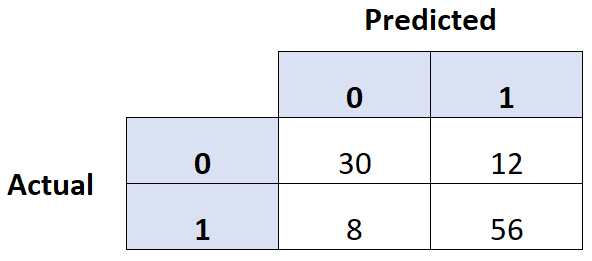
Das folgende Schritt-für-Schritt-Beispiel zeigt, wie man in R eine Verwirrungsmatrix erstellt.

Schritt 1: Passen Sie das logistische Regressionsmodell an

Für dieses Beispiel verwenden wir den Standarddatensatz aus dem ISLR- Paket. Wir nutzen den Studentenstatus, den Kontostand und das Jahreseinkommen, um die Wahrscheinlichkeit vorherzusagen, dass eine bestimmte Person mit ihrem Darlehen in Verzug gerät.

Der folgende Code zeigt, wie ein logistisches Regressionsmodell an diesen Datensatz angepasst wird:

 #load necessary packages
library (caret)
library (InformationValue)
library (ISLR)

#load dataset
data <-Default

#split dataset into training and testing set
set. seeds (1)
sample <- sample(c(TRUE, FALSE), nrow(data), replace= TRUE , prob=c(0.7,0.3))
train <- data[sample, ]
test <- data[!sample, ]

#fit logistic regression model
model <- glm(default~student+balance+income, family=" binomial ", data=train)

Schritt 2: Erstellen Sie die Verwirrungsmatrix

Als Nächstes verwenden wir die Funktion „confusionMatrix()“ aus dem Paket „caret “, um eine Konfusionsmatrix zu erstellen:

 #use model to predict probability of default
predicted <- predict(model, test, type="response")

#convert defaults from "Yes" and "No" to 1's and 0's
test$default <- ifelse(test$default==" Yes ", 1, 0)

#find optimal cutoff probability to use to maximize accuracy
optimal <- optimalCutoff(test$default, predicted)[1]

#create confusion matrix
confusionMatrix(test$default, predicted)

     0 1
0 2912 64
1 21 39

Schritt 3: Bewerten Sie die Verwirrungsmatrix

Mit der Verwirrungsmatrix können wir auch die folgenden Metriken berechnen:

• Sensitivität: Die „wahre Positivitätsrate“ – der Prozentsatz der Personen, bei denen das Modell korrekt vorhergesagt hat, dass sie ausfallen würden.
• Spezifität: Die „wahre Negativrate“ – der Prozentsatz der Personen, bei denen das Modell korrekt vorhergesagt hat, dass sie nicht ausfallen würden.
• Gesamtfehlklassifizierungsrate: Prozentsatz der gesamten vom Modell vorgenommenen Fehlklassifizierungen.

Der folgende Code zeigt, wie diese Metriken berechnet werden:

 #calculate sensitivity
sensitivity(test$default, predicted)

[1] 0.3786408

#calculate specificity
specificity(test$default, predicted)

[1] 0.9928401

#calculate total misclassification error rate
misClassError(test$default, predicted, threshold =optimal)

[1] 0.027

Die Gesamtklassifizierungsfehlerrate beträgt für dieses Modell 2,7 % .

Im Allgemeinen gilt: Je niedriger diese Rate, desto besser kann das Modell die Ergebnisse vorhersagen. Dieses spezielle Modell erweist sich daher als sehr effektiv bei der Vorhersage, ob eine Person zahlungsunfähig wird oder nicht.