So führen sie eine mehrdimensionale skalierung in python durch

In der Statistik ist die mehrdimensionale Skalierung eine Möglichkeit, die Ähnlichkeit von Beobachtungen in einem Datensatz in einem abstrakten kartesischen Raum (normalerweise 2D-Raum) zu visualisieren.

Der einfachste Weg, eine mehrdimensionale Skalierung in Python durchzuführen, ist die Verwendung der Funktion MDS() des Submoduls sklearn.manifold .

Das folgende Beispiel zeigt, wie Sie diese Funktion in der Praxis nutzen können.

Beispiel: Mehrdimensionale Skalierung in Python

Angenommen, wir haben den folgenden Pandas-DataFrame, der Informationen über verschiedene Basketballspieler enthält:

 import pandas as pd

#create DataFrane
df = pd. DataFrame ({' player ': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K '],
                   ' points ': [4, 4, 6, 7, 8, 14, 16, 19, 25, 25, 28],
                   ' assists ': [3, 2, 2, 5, 4, 8, 7, 6, 8, 10, 11],
                   ' blocks ': [7, 3, 6, 7, 5, 8, 8, 4, 2, 2, 1],
                   ' rebounds ': [4, 5, 5, 6, 5, 8, 10, 4, 3, 2, 2]})

#set player column as index column
df = df. set_index (' player ')

#view Dataframe
print (df)

        points assists blocks rebounds
player                                   
A 4 3 7 4
B 4 2 3 5
C 6 2 6 5
D 7 5 7 6
E 8 4 5 5
F 14 8 8 8
G 16 7 8 10
H 19 6 4 4
I 25 8 2 3
D 25 10 2 2
K 28 11 1 2

Wir können den folgenden Code verwenden, um eine mehrdimensionale Skalierung mit der Funktion MDS() des Moduls sklearn.manifold durchzuführen:

 from sklearn. manifold import MDS

#perform multi-dimensional scaling
mds = MDS(random_state= 0 )
scaled_df = mds. fit_transform (df)

#view results of multi-dimensional scaling
print (scaled_df)

[[ 7.43654469 8.10247222]
 [4.13193821 10.27360901]
 [5.20534681 7.46919526]
 [6.22323046 4.45148627]
 [3.74110999 5.25591459]
 [3.69073384 -2.88017811]
 [3.89092087 -5.19100988]
 [ -3.68593169 -3.0821144 ]
 [ -9.13631889 -6.81016012]
 [ -8.97898385 -8.50414387]
 [-12.51859044 -9.08507097]]

Jede Zeile des ursprünglichen DataFrame wurde auf eine (x, y)-Koordinate reduziert.

Wir können den folgenden Code verwenden, um diese Koordinaten im 2D-Raum zu visualisieren:

 import matplotlib.pyplot as plt

#create scatterplot
plt. scatter (scaled_df[:,0], scaled_df[:,1])

#add axis labels
plt. xlabel (' Coordinate 1 ')
plt. ylabel (' Coordinate 2 ')

#add lables to each point
for i, txt in enumerate( df.index ):
    plt. annotate (txt, (scaled_df[:,0][i]+.3, scaled_df[:,1][i]))

#display scatterplot
plt. show ()

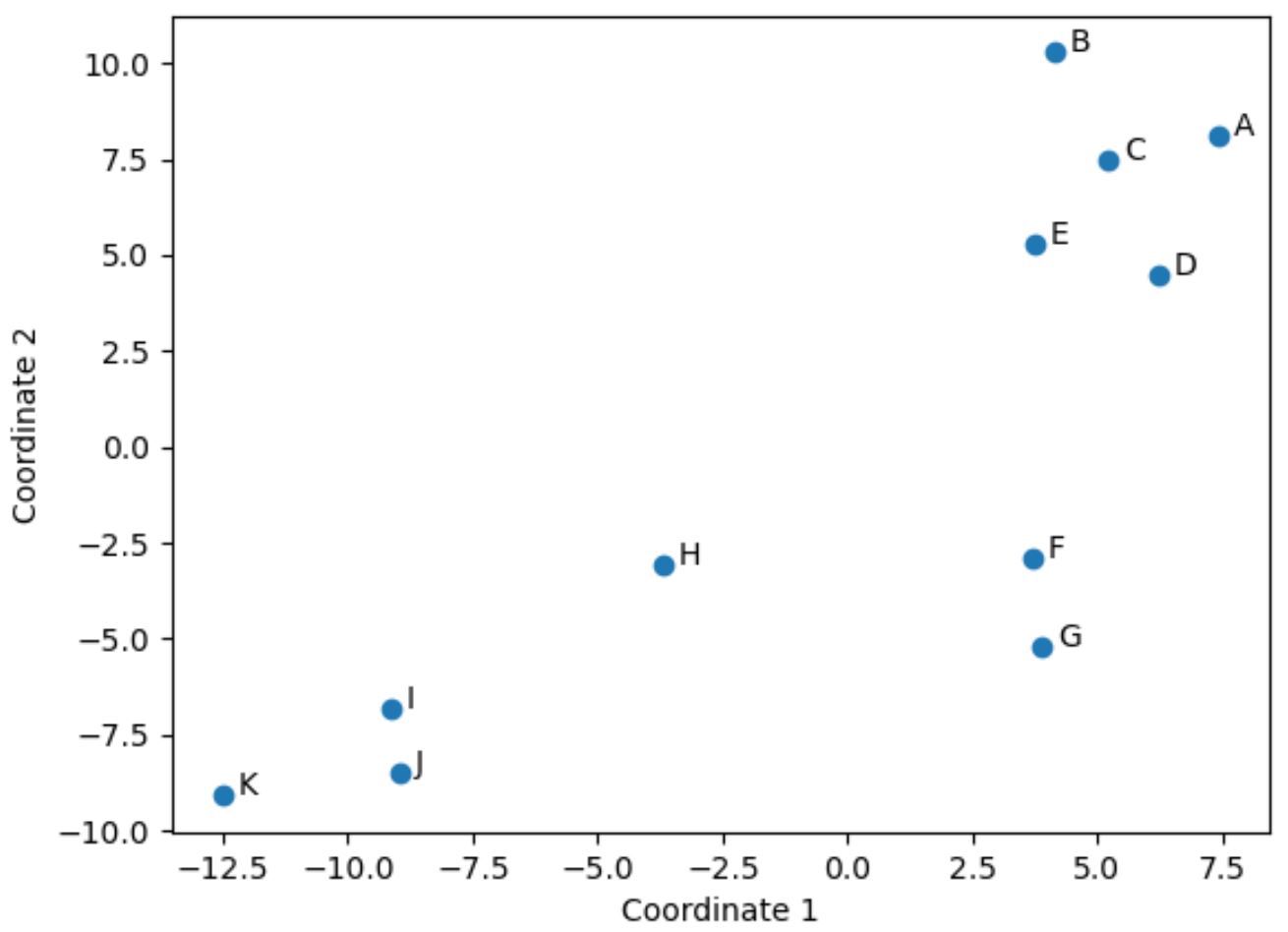
Spieler im ursprünglichen DataFrame, die ähnliche Werte in den ursprünglichen vier Spalten (Punkte, Assists, Blocks und Rebounds) haben, liegen im Plot nahe beieinander.

Beispielsweise sind die Spieler F und G eng beieinander. Hier sind ihre Werte aus dem ursprünglichen DataFrame:

 #select rows with index labels 'F' and 'G'
df. loc [[' F ',' G ']]

        points assists blocks rebounds
player				
F 14 8 8 8
G 16 7 8 10

Ihre Werte für Punkte, Assists, Blocks und Rebounds sind alle ziemlich ähnlich, was erklärt, warum sie im 2D-Plot so nahe beieinander liegen.

Betrachten Sie im Gegensatz dazu die Spieler B und K , die in der Handlung weit voneinander entfernt sind.

Wenn wir uns auf ihre Werte im ursprünglichen DataFrame beziehen, können wir sehen, dass sie ziemlich unterschiedlich sind:

 #select rows with index labels 'B' and 'K'
df. loc [[' B ',' K ']]

        points assists blocks rebounds
player				
B 4 2 3 5
K 28 11 1 2

Das 2D-Diagramm ist also eine gute Möglichkeit, zu visualisieren, wie ähnlich sich die einzelnen Spieler über alle Variablen im DataFframe hinweg sind.

Spieler mit ähnlichen Statistiken werden eng beieinander gruppiert, während Spieler mit sehr unterschiedlichen Statistiken in der Handlung weiter voneinander entfernt sind.

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie Sie andere häufige Aufgaben in Python ausführen:

So normalisieren Sie Daten in Python
So entfernen Sie Ausreißer in Python
So testen Sie die Normalität in Python