R-vielfaches oder r-quadrat: was ist der unterschied?

Wenn Sie ein Regressionsmodell mit den meisten Statistikprogrammen anpassen, werden Sie im Ergebnis häufig die folgenden zwei Werte bemerken:

Multiples R: der multiple Korrelationskoeffizient zwischen drei oder mehr Variablen.

R-Quadrat: Dies wird als (Multiple R) ² berechnet und stellt den Anteil der Varianz in der Antwortvariablen eines Regressionsmodells dar, der durch die Prädiktorvariablen erklärt werden kann. Dieser Wert variiert zwischen 0 und 1.

In der Praxis sind wir oft am R-Quadrat-Wert interessiert, weil er uns sagt, wie nützlich die Prädiktorvariablen für die Vorhersage des Werts der Antwortvariablen sind.

Jedes Mal, wenn wir dem Modell jedoch eine neue Prädiktorvariable hinzufügen, erhöht sich das R-Quadrat garantiert, auch wenn die Prädiktorvariable nicht nützlich ist.

Das angepasste R-Quadrat ist eine modifizierte Version des R-Quadrats, die die Anzahl der Prädiktoren in einem Regressionsmodell berücksichtigt. Es wird wie folgt berechnet:

Angepasstes R ² = 1 – [(1-R ² )*(n-1)/(nk-1)]

Gold:

• R ² : Das R ² des Modells
• n : Die Anzahl der Beobachtungen
• k : Die Anzahl der Prädiktorvariablen

Da das R-Quadrat immer zunimmt, wenn Sie einem Modell mehr Prädiktoren hinzufügen, kann das angepasste R-Quadrat als Metrik dienen, die Ihnen sagt, wie nützlich ein Modell ist, angepasst auf der Grundlage der Anzahl der Prädiktoren in einem Modell .

Um jeden dieser Begriffe besser zu verstehen, betrachten Sie das folgende Beispiel.

Beispiel: Multiples R, R-Quadrat und angepasstes R-Quadrat

Angenommen, wir haben den folgenden Datensatz, der die folgenden drei Variablen für 12 verschiedene Schüler enthält:

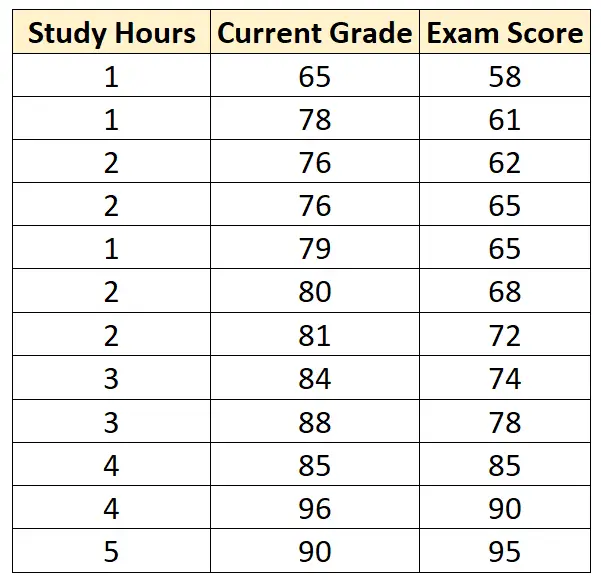
Angenommen, wir passen ein multiples lineares Regressionsmodell an, indem wir die Lernstunden und die aktuelle Note als Prädiktorvariablen und die Prüfungspunktzahl als Antwortvariable verwenden und das folgende Ergebnis erhalten:

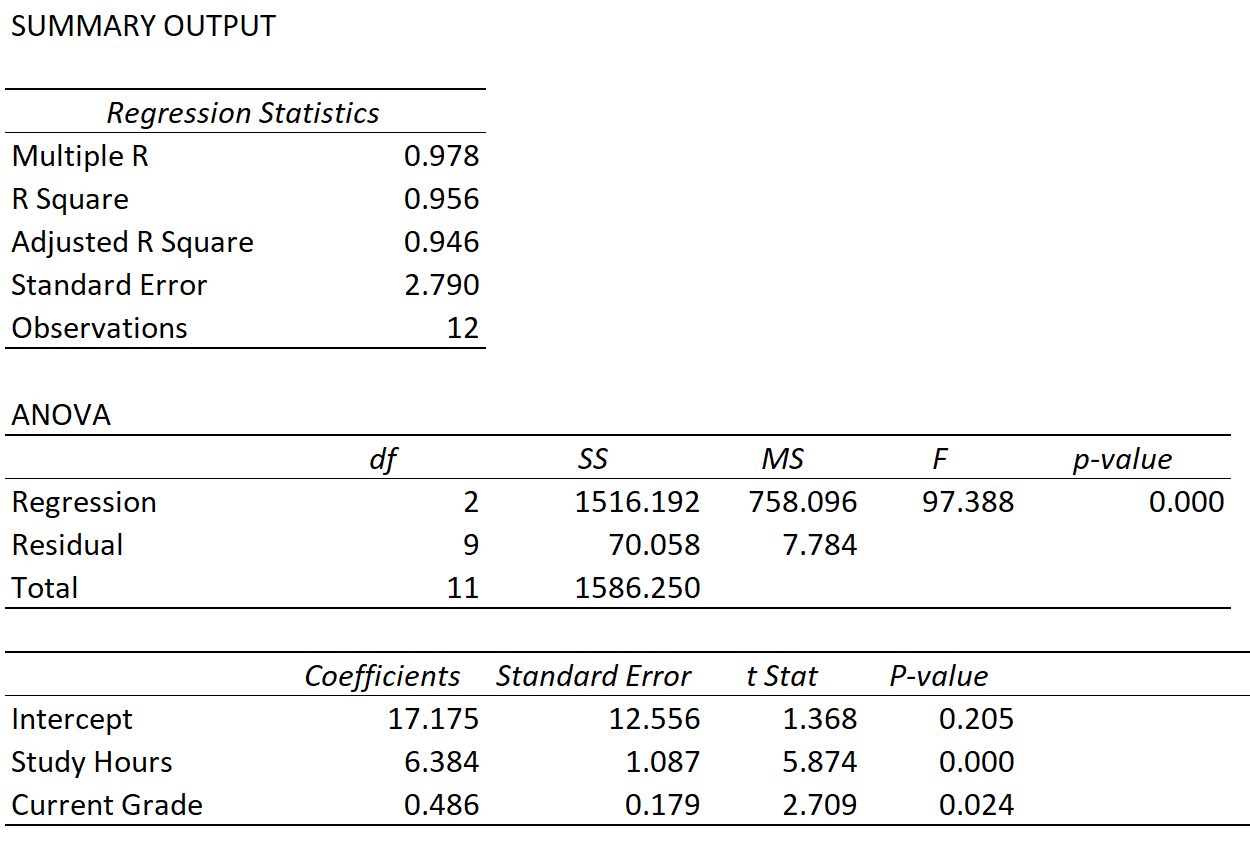
Wir können die Werte der folgenden drei Metriken beobachten:

Mehrfaches R: 0,978 . Dies stellt die mehrfache Korrelation zwischen der Antwortvariablen und den beiden Prädiktorvariablen dar.

R-Quadrat: 0,956 . Dies wird berechnet als (Multiple R) ² = (0,978) ² = 0,956. Dies zeigt uns, dass 95,6 % der Abweichungen bei den Prüfungsergebnissen durch die Anzahl der Lernstunden und die aktuelle Note der Studierenden im Kurs erklärt werden können.

Bereinigtes R-Quadrat: 0,946 . Dies wird wie folgt berechnet:

Angepasstes R ² = 1 – [(1-R ² )*(n-1)/(nk-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0,946.

Dies stellt den R-Quadrat-Wert dar, angepasst an die Anzahl der Prädiktorvariablen im Modell .

Dieses Maß wäre nützlich, wenn wir beispielsweise ein anderes Regressionsmodell mit 10 Prädiktoren anpassen und feststellen würden, dass das angepasste R-Quadrat dieses Modells 0,88 beträgt. Dies würde darauf hinweisen, dass das Regressionsmodell mit nur zwei Prädiktoren besser ist, da es einen höheren angepassten R-Quadrat-Wert aufweist.

Zusätzliche Ressourcen

Einführung in die multiple lineare Regression
Was ist ein guter R-Quadrat-Wert?