Wie man die methode der kleinsten quadrate in r verwendet

Die Methode der kleinsten Quadrate ist eine Methode, mit der wir die Regressionslinie finden können, die am besten zu einem bestimmten Datensatz passt.

Um die Methode der kleinsten Quadrate zum Anpassen einer Regressionslinie in R zu verwenden, können wir die Funktion lm() verwenden.

Diese Funktion verwendet die folgende grundlegende Syntax:

 model <- lm(response ~ predictor, data=df)

Das folgende Beispiel zeigt, wie diese Funktion in R verwendet wird.

Beispiel: Methode der kleinsten Quadrate in R

Angenommen, wir haben den folgenden Datenrahmen in R, der die Anzahl der gelernten Stunden und das entsprechende Prüfungsergebnis für 15 Schüler einer Klasse anzeigt:

 #create data frame
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Mit der Funktion lm() können wir mithilfe der Methode der kleinsten Quadrate eine Regressionslinie an diese Daten anpassen:

 #use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Aus den Werten in der Spalte „Geschätztes Ergebnis“ können wir die folgende angepasste Regressionslinie schreiben:

Prüfungsergebnis = 65,334 + 1,982 (Stunden)

So interpretieren Sie jeden Koeffizienten im Modell:

• Intercept : Für einen Studenten, der 0 Stunden lernt, beträgt die erwartete Prüfungspunktzahl 65,334 .
• Stunden : Für jede weitere gelernte Stunde erhöht sich die erwartete Prüfungspunktzahl um 1.982 .

Mithilfe dieser Gleichung können wir die Prüfungsnote abschätzen, die ein Student auf der Grundlage seiner gelernten Stunden erhalten wird.

Wenn ein Student beispielsweise 5 Stunden lernt, würden wir schätzen, dass sein Prüfungsergebnis 75,244 beträgt:

Prüfungsergebnis = 65,334 + 1,982(5) = 75,244

Schließlich können wir ein Streudiagramm der Originaldaten erstellen, wobei die angepasste Regressionslinie dem Diagramm überlagert ist:

 #create scatter plot of data
plot(df$hours, df$score, pch=16, col=' steelblue ')

#add fitted regression line to scatter plot
abline(model)

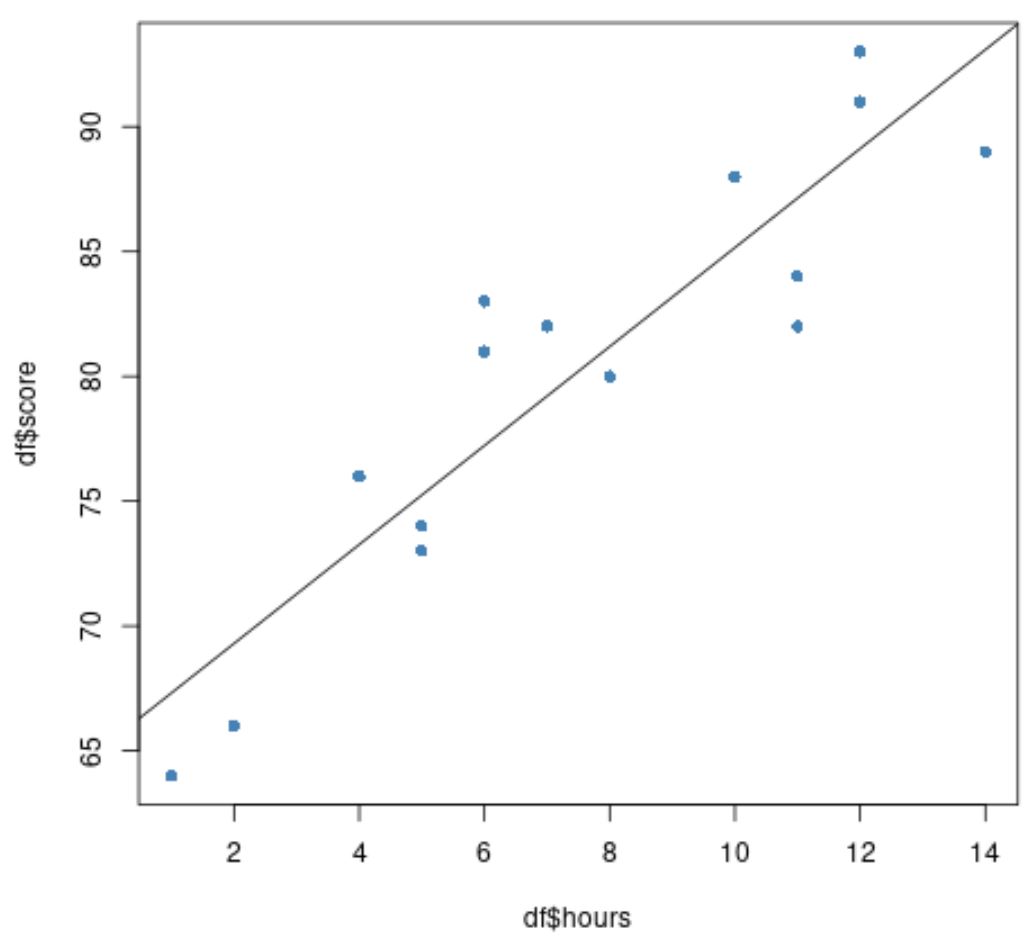
Die blauen Kreise stellen die Daten dar und die schwarze Linie stellt die angepasste Regressionslinie dar.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in R ausführen:

So erstellen Sie ein Residuendiagramm in R
So testen Sie die Multikollinearität in R
So führen Sie eine Kurvenanpassung in R durch