So ermitteln sie den mittelwert einer wahrscheinlichkeitsverteilung: mit beispielen

Eine Wahrscheinlichkeitsverteilung gibt uns die Wahrscheinlichkeit an, mit der eine Zufallsvariable bestimmte Werte annimmt.

Die folgende Wahrscheinlichkeitsverteilung sagt uns beispielsweise die Wahrscheinlichkeit, dass eine bestimmte Fußballmannschaft in einem bestimmten Spiel eine bestimmte Anzahl Tore schießt:

Hinweis: Die Wahrscheinlichkeiten in einer gültigen Wahrscheinlichkeitsverteilung summieren sich immer auf 1. Wir können bestätigen, dass diese Wahrscheinlichkeitsverteilung gültig ist: 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1.

Um den Mittelwert (manchmal auch „erwarteter Wert“ genannt) einer Wahrscheinlichkeitsverteilung zu ermitteln, können wir die folgende Formel verwenden:

 Mean (Or "Expected Value") of a Probability Distribution:

μ = Σx * P(x)

where:
•x: Data value
    •P(x): Probability of value

Betrachten Sie zum Beispiel unsere Wahrscheinlichkeitsverteilung für die Fußballmannschaft:

Die durchschnittliche Anzahl der Tore der Fußballmannschaft würde wie folgt berechnet:

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 Tore.

Die folgenden Beispiele zeigen, wie der Durchschnitt einer Wahrscheinlichkeitsverteilung in einigen anderen Szenarien berechnet wird.

Beispiel 1: Durchschnittliche Anzahl von Fahrzeugpannen

Die folgende Wahrscheinlichkeitsverteilung gibt Auskunft über die Wahrscheinlichkeit, dass bei einem bestimmten Fahrzeug über einen Zeitraum von 10 Jahren eine bestimmte Anzahl von Batterieausfällen auftritt:

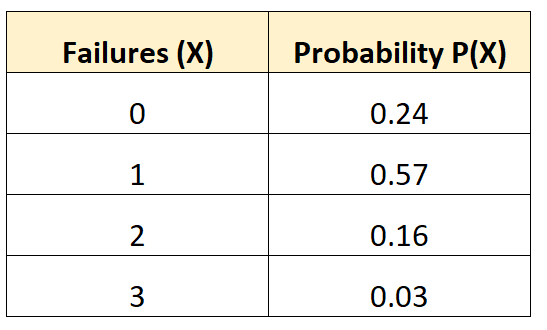
Frage: Wie hoch ist die durchschnittliche Anzahl an Pannen, die bei diesem Fahrzeug zu erwarten sind?

Lösung: Die durchschnittliche Anzahl der erwarteten Ausfälle wird wie folgt berechnet:

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 Ausfälle.

Beispiel 2: durchschnittliche Anzahl an Siegen

Die folgende Wahrscheinlichkeitsverteilung sagt uns die Wahrscheinlichkeit, dass eine bestimmte Basketballmannschaft eine bestimmte Anzahl Spiele in einem Turnier gewinnt:

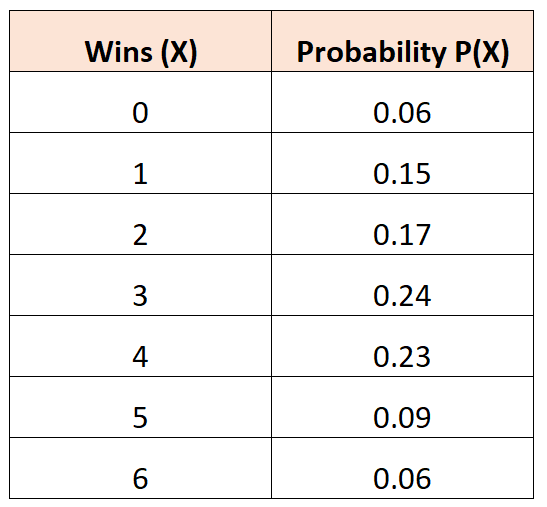
Frage: Wie hoch ist die durchschnittliche Anzahl an Siegen, die für dieses Team erwartet werden?

Lösung: Die durchschnittliche Anzahl der erwarteten Siege wird wie folgt berechnet:

μ = 0*0,06 + 1*0,15 + 2*0,17 + 3*0,24 + 4*0,23 + 5*0,09 + 6*0,06 = 2,94 Siege.

Beispiel 3: durchschnittliche Anzahl an Verkäufen

Die folgende Wahrscheinlichkeitsverteilung sagt uns die Wahrscheinlichkeit, dass ein bestimmter Verkäufer im kommenden Monat eine bestimmte Anzahl von Verkäufen tätigen wird:

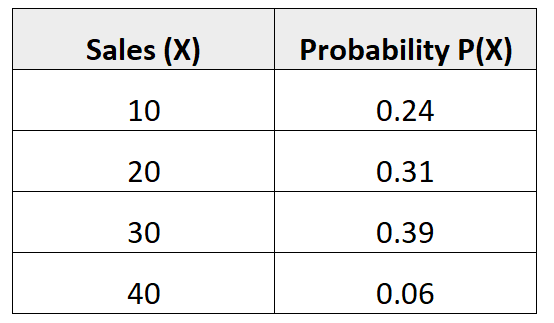
Frage: Wie hoch ist die durchschnittliche Anzahl an Verkäufen, die für diesen Verkäufer im kommenden Monat erwartet werden?

Lösung: Die durchschnittliche Anzahl der erwarteten Verkäufe wird wie folgt berechnet:

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 verschmutzt.

Bonus: Wahrscheinlichkeitsverteilungsrechner

Mit diesem Rechner können Sie den Mittelwert einer beliebigen Wahrscheinlichkeitsverteilung automatisch berechnen.