Die beziehung zwischen mittelwert und standardabweichung (mit beispiel)
Der Mittelwert stellt den Durchschnittswert in einem Datensatz dar.
Es wird wie folgt berechnet:
Stichprobenmittelwert = Σx i / n
Gold:
- Σ: Ein Symbol, das „Summe“ bedeutet
- x i : Die i- te Beobachtung in einem Datensatz
- n: die Gesamtzahl der Beobachtungen im Datensatz
Die Standardabweichung stellt die Verteilung der Werte in einem Datensatz relativ zum Mittelwert dar.
Es wird wie folgt berechnet:
Stichprobenstandardabweichung = √ Σ(x i – x bar ) 2 / (n-1)
Gold:
- Σ: Ein Symbol, das „Summe“ bedeutet
- x i : der i-te Wert der Stichprobe
- x bar : Der Stichprobenmittelwert
- n: Die Stichprobengröße
Beachten Sie die Beziehung zwischen dem Mittelwert und der Standardabweichung: Der Mittelwert wird in der Formel zur Berechnung der Standardabweichung verwendet .
Tatsächlich können wir die Standardabweichung einer Stichprobe nicht berechnen, es sei denn, wir kennen den Stichprobenmittelwert.
Das folgende Beispiel zeigt, wie der Stichprobenmittelwert und die Stichprobenstandardabweichung für einen Datensatz in der Praxis berechnet werden.
Beispiel: Berechnen des Mittelwerts und der Standardabweichung für einen Datensatz
Nehmen wir an, wir haben den folgenden Datensatz, der die von 10 verschiedenen Basketballspielern erzielten Punkte zeigt:
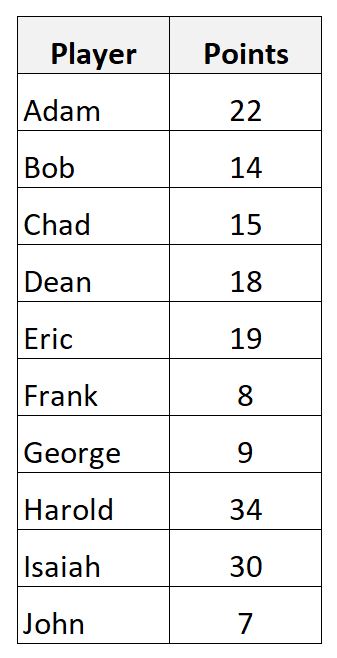Den Stichprobendurchschnitt der erzielten Punkte können wir mit der folgenden Formel berechnen:
- Stichprobenmittelwert = Σx i / n
- Stichprobendurchschnitt = (22+14+15+18+19+8+9+34+30+7) / 10
- Stichprobenmittelwert = 17,6
Der Stichprobendurchschnitt der erzielten Punkte beträgt 17,6 . Dies stellt die durchschnittliche Punktzahl aller Spieler dar.
Sobald wir den Stichprobenmittelwert kennen, können wir ihn in die Formel einfügen, um die Stichprobenstandardabweichung zu berechnen:
- Stichprobenstandardabweichung = √ Σ(x i – x bar ) 2 / (n-1)
- Stichprobenstandardabweichung = √ ((22-17,6) 2 + (14-17,6) 2 + (15-17,6) 2 + (18-17,6) 2 + (19-17,6) 6) 2 + (8-17,6) 2 + (9 -17,6) 2 + (34-17,6) 2 + (30-17,6) 2 + (7-17,6) 2 ) / (10-1)
- Stichprobenstandardabweichung = 9,08
Die Stichprobenstandardabweichung beträgt 9,08 . Dies stellt den durchschnittlichen Abstand zwischen jedem Punktwert und dem Stichprobenpunktdurchschnitt dar.
Es ist nützlich, sowohl den Mittelwert als auch die Standardabweichung eines Datensatzes zu kennen, da jede Metrik etwas anderes sagt.
Der Durchschnitt gibt uns eine Vorstellung davon, wo der „zentrale“ Wert eines Datensatzes liegt.
Die Standardabweichung gibt uns eine Vorstellung von der Verteilung der Werte um den Mittelwert in einem Datensatz. Je höher der Standardabweichungswert ist, desto stärker sind die Werte in einer Stichprobe gestreut.
Durch die Kenntnis dieser beiden Werte können wir viel über die Werteverteilung in einem Datensatz lernen.
Zusätzliche Ressourcen
Die folgenden Tutorials bieten zusätzliche Informationen zum Mittelwert und zur Standardabweichung:
Warum ist der Durchschnitt in der Statistik wichtig?
Warum ist die Standardabweichung in der Statistik wichtig?
So berechnen Sie den Mittelwert und die Standardabweichung in Excel
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen