Mittelwert, median und modus

Von Dr. Benjamin Anderson August 5, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erläutert, was Mittelwert, Median und Modus sind. Sie erfahren, wie Sie den Mittelwert, den Median und den Modus ermitteln, wofür sie verwendet werden und was der Unterschied zwischen diesen drei statistischen Maßen ist. Darüber hinaus können Sie mit dem Online-Rechner am Ende den Mittelwert, den Median und den Modus jeder statistischen Stichprobe berechnen.

Was ist Mittelwert, Median und Modus?

Mittelwert, Median und Modus sind statistische Maße der zentralen Position. Mit anderen Worten: Mittelwert, Median und Modus sind Werte, die bei der Definition einer statistischen Stichprobe helfen, insbesondere geben sie an, was ihre zentralen Werte sind.

Mittelwert, Median und Modus sind wie folgt definiert:

Mittelwert : ist der Durchschnitt aller Daten in der Stichprobe.
Median : Dies ist der Mittelwert aller Daten, sortiert vom kleinsten zum größten.
Modus : Dies ist der am häufigsten wiederholte Wert im Datensatz.

Diese drei statistischen Maße werden im Folgenden näher erläutert.

Halb

Um den Durchschnitt zu berechnen, addieren Sie alle Werte und teilen Sie sie dann durch die Gesamtzahl der Daten. Die Formel für den Durchschnitt lautet daher wie folgt:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}$

Mit dem Rechner unten können Sie den Mittelwert, den Median und den Modus eines beliebigen Datensatzes berechnen.

Das durchschnittliche Symbol ist ein horizontales Band über dem Buchstaben x

$(\overline{x}).$

Sie können den Stichprobenmittelwert auch mit dem Mittelwertsymbol vom Grundgesamtheitsmittelwert unterscheiden: Der Mittelwert einer Stichprobe wird mit dem Symbol ausgedrückt

$\overline{x}$

, während der Durchschnitt einer Bevölkerung den griechischen Buchstaben verwendet

$\mu.$

Der Durchschnitt wird auch als arithmetisches Mittel oder Durchschnitt bezeichnet. Darüber hinaus entspricht der Mittelwert einer statistischen Verteilung ihrem mathematischen Erwartungswert.

Durchschnittliches Beispiel

Ein Schüler hat im Laufe eines Schuljahres folgende Noten erreicht: in Mathematik eine 9, in Sprache eine 7, in Geschichte eine 6, in Wirtschaftswissenschaften eine 8 und in Naturwissenschaften eine 7,5. Was ist der Durchschnitt aller Ihrer Noten?

Um den arithmetischen Durchschnitt zu ermitteln, müssen wir alle Noten addieren und dann durch die Gesamtzahl der Fächer im Kurs dividieren, also 5. Daher wenden wir die Formel für den arithmetischen Durchschnitt an:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}$

Wir setzen die Daten in die Formel ein und berechnen das arithmetische Mittel:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

Wie Sie sehen, wird im arithmetischen Mittel jedem Wert das gleiche Gewicht zugewiesen, das heißt, jedes Datenelement hat im Ganzen das gleiche Gewicht.

Median

Der Median ist der Mittelwert aller Daten, geordnet vom kleinsten zum größten. Mit anderen Worten: Der Median teilt den geordneten Datensatz in zwei gleiche Teile.

Die Berechnung des Medians hängt davon ab, ob die Gesamtzahl der Daten gerade oder ungerade ist:

Wenn die Gesamtzahl der Daten ungerade ist, ist der Median der Wert, der genau in der Mitte der Daten liegt. Das heißt der Wert, der an Position (n+1)/2 der sortierten Daten steht.

$Me=x_{\frac{n+1}{2}$

Wenn die Gesamtzahl der Datenpunkte gerade ist, ist der Median der Durchschnitt der beiden Datenpunkte in der Mitte. Das heißt das arithmetische Mittel der Werte, die an den Positionen n/2 und n/2+1 der geordneten Daten gefunden werden.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Gold

$n$

ist die Gesamtzahl der Datenelemente in der Stichprobe.

Der Begriff Me wird oft als Symbol verwendet, um anzuzeigen, dass ein Wert der Median aller Beobachtungen ist.

Mit dem Rechner unten können Sie den Mittelwert, den Median und den Modus eines beliebigen Datensatzes berechnen.

Median-Beispiel

Finden Sie den Median der folgenden Daten: 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5

Bevor wir Berechnungen durchführen, müssen wir zunächst die Daten klassifizieren, d. h. wir ordnen die Zahlen vom kleinsten zum größten an.

$1 \ 2 \ 3 \ 4 \ 4 \ 4 \ 5 \ 6 \ 7 \ 8 \ 8$

In diesem Fall haben wir 11 Beobachtungen, daher ist die Gesamtzahl der Daten ungerade. Daher wenden wir die folgende Formel an, um die Position des Medians zu berechnen:

$\cfrac{n+1}{2}=\cfrac{11+1}{2}=6$

Als Median werden also die an sechster Stelle stehenden Daten herangezogen, was in diesem Fall dem Wert 4 entspricht.

$Me=x_6=4$

Mode

In der Statistik ist der Modus der Wert im Datensatz, der die höchste absolute Häufigkeit aufweist, d. h. der Modus ist der am häufigsten wiederholte Wert in einem Datensatz.

Um den Modus eines statistischen Datensatzes zu berechnen, zählen Sie daher einfach, wie oft jedes Datenelement in der Stichprobe vorkommt. Die am häufigsten wiederholten Daten ergeben den Modus.

Der Modus kann auch als statistischer Modus oder Modalwert bezeichnet werden. Wenn Daten in Intervalle gruppiert werden, ist das am häufigsten wiederholte Intervall das Modalintervall oder die Modalklasse .

Im Allgemeinen wird der Begriff Mo als Symbol für den statistischen Modus verwendet, beispielsweise ist der Verteilungsmodus X Mo(X).

Je nach Anzahl der am häufigsten wiederholten Werte können drei Arten von Modi unterschieden werden:

Unimodaler Modus : Es gibt nur einen Wert mit der maximalen Anzahl an Wiederholungen. Zum Beispiel [1, 4, 2, 4, 5, 3].
Bimodaler Modus : Die maximale Anzahl an Wiederholungen erfolgt bei zwei unterschiedlichen Werten, und beide Werte werden gleich oft wiederholt. Zum Beispiel [2, 6, 7, 2, 3, 6, 9].
Multimodaler Modus : Drei oder mehr Werte haben die gleiche maximale Wiederholungszahl. Zum Beispiel [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].

Mit dem Rechner unten können Sie den Mittelwert, den Median und den Modus eines beliebigen Datensatzes berechnen.

Modebeispiel

Welchen Modus hat der folgende Datensatz?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

Die Zahlen sind nicht in der richtigen Reihenfolge, also sortieren wir sie zunächst. Dieser Schritt ist nicht zwingend erforderlich, hilft Ihnen aber dabei, Mode leichter zu finden.

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

Die Zahlen 2 und 9 erscheinen zweimal, aber die Zahl 5 wird dreimal wiederholt. Daher ist der Modus der Datenreihe Nummer 5.

$Mo=5$

Gelöste Übung zu Mittelwert, Median und Modus

Nachdem Sie nun den Mittelwert, den Median und den Modus kennen, finden Sie unten eine ausführliche Übung zu diesen statistischen Maßen, damit Sie genau sehen können, wie sie berechnet werden.

Ermitteln Sie Mittelwert, Median und Modus des folgenden statistischen Datensatzes:

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

Um den Durchschnitt der Daten zu ermitteln, müssen wir alles addieren und dann durch die Gesamtzahl der Daten dividieren, also 30:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^N x_i}{N}=\frac{192}{30}=6,4$

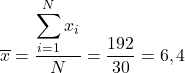
Zweitens ermitteln wir den Stichprobenmedian. Also ordnen wir alle Zahlen in aufsteigender Reihenfolge an:

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

In diesem Fall ist die Gesamtzahl der Daten gerade, daher müssen die beiden zentralen Positionen berechnet werden, zwischen denen der Median ermittelt wird. Hierzu verwenden wir die folgenden zwei Formeln:

$\cfrac{n}{2}=\cfrac{30}{2}=15$

$\cfrac{n}{2}+1=\cfrac{30}{2}+1=16$

Der Median liegt also zwischen der fünfzehnten und sechzehnten Stelle, was den Werten 6 bzw. 7 entspricht. Genauer gesagt entspricht der Median dem Durchschnitt dieser Werte:

$Me=\cfrac{x_{15}+x_{16}}{2}=\cfrac{6+7}{2}=6,5$

Um schließlich den Modus zu finden, müssen Sie nur noch zählen, wie oft jede Zahl erscheint. Wie Sie sehen, erscheinen Nummer 6 und Nummer 8 insgesamt viermal, was der maximalen Anzahl an Wiederholungen entspricht. Daher handelt es sich in diesem Fall um einen bimodalen Modus und die beiden Zahlen sind der Modus des Datensatzes:

$Mo=\{ 6 \ ; \ 8\}$