Mittlerer unterschied
In diesem Artikel wird erklärt, was eine mittlere Abweichung ist und wie sie berechnet wird. Außerdem finden Sie konkrete Beispiele zur Berechnung der durchschnittlichen Abweichung. Darüber hinaus können Sie mit einem Online-Rechner die durchschnittliche Abweichung jedes statistischen Datensatzes berechnen.
Was ist die mittlere Abweichung?
Die mittlere Abweichung , auch mittlere absolute Abweichung genannt, ist ein Maß für die statistische Streuung.
Die mittlere Abweichung eines Datensatzes ist der Durchschnitt der absoluten Abweichungen . Daher ist die durchschnittliche Abweichung gleich der Summe der Abweichungen jedes Datenelements vom arithmetischen Mittel geteilt durch die Gesamtzahl der Datenelemente.
Mit anderen Worten lautet die Formel für die durchschnittliche Abweichung wie folgt:

👉 Mit dem Rechner unten können Sie die durchschnittliche Abweichung eines beliebigen Datensatzes berechnen.
In der Statistik wird die mittlere Abweichung auch mittlere absolute Abweichung genannt.
Die Interpretation der durchschnittlichen Abweichung erfolgt wie folgt: Je größer der Wert der durchschnittlichen Abweichung, desto weiter sind die Daten im Durchschnitt vom arithmetischen Mittel entfernt; Umgekehrt gilt: Je geringer die durchschnittliche Abweichung, desto näher liegt der Wert. Die Daten sind. Die durchschnittliche Abweichung gibt also die Streuung einer Datenreihe an.
Andere als verteilt betrachtete Maße sind Bereich, Interquartilbereich, Standardabweichung (oder Standardabweichung), Varianz und Variationskoeffizient.
So berechnen Sie die durchschnittliche Abweichung
Um die durchschnittliche Abweichung einer Datenreihe zu berechnen, müssen folgende Schritte befolgt werden:
- Berechnen Sie das arithmetische Mittel des statistischen Datensatzes.
- Berechnen Sie die Abweichung jedes Datenpunkts vom Mittelwert, definiert als absoluter Wert der Differenz zwischen den Daten und dem Mittelwert.
- Addieren Sie alle im vorherigen Schritt berechneten Differenzen.
- Teilen Sie durch die Gesamtzahl der Daten. Das erhaltene Ergebnis ist die durchschnittliche Abweichung der Datenreihe.
Zusammenfassend lautet die Formel, die zur Ermittlung der durchschnittlichen Abweichung angewendet werden muss:
![]()
Beispiel für die Berechnung der durchschnittlichen Abweichung
Unter Berücksichtigung der Definition der mittleren Abweichung finden Sie unten ein Schritt-für-Schritt-Lösungsbeispiel für die Berechnung der mittleren Abweichung einer statistischen Stichprobe. Auf diese Weise verstehen Sie besser, wie Sie die durchschnittliche Abweichung ermitteln.
- Ein Analyst untersucht die wirtschaftlichen Ergebnisse eines Unternehmens im vergangenen Jahr und verfügt über Informationen über den Gewinn, den das Unternehmen in jedem Quartal dieses Jahres erzielt hat: 2, 3, 7 und 5 Millionen Dollar. Wie groß ist die durchschnittliche Abweichung der Daten?
Zuerst müssen wir die Daten mitteln, also summieren und dividieren wir durch die Gesamtzahl der Beobachtungen (4):
![]()
Nachdem wir das arithmetische Mittel berechnet haben, verwenden wir die Formel für die mittlere Abweichung:
![]()
Wir setzen die Daten in die Formel ein:
![]()
Wir führen die Berechnungen im Zähler durch:
![]()
![]()
![]()
Und schließlich dividieren wir durch die Gesamtzahl der Daten, um die durchschnittliche Abweichung der Stichprobe zu erhalten:
![]()
Durchschnittlicher Abweichungsrechner
Geben Sie eine Reihe statistischer Daten in den folgenden Rechner ein, um die durchschnittliche Abweichung zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.
Durchschnittliche Abweichung für gruppierte Daten
Um die mittlere Abweichung von in Intervallen gruppierten Daten zu berechnen, müssen die folgenden Schritte befolgt werden:
- Bestimmen Sie das arithmetische Mittel des statistischen Datensatzes. Da die Daten gruppiert sind, lautet der Ausdruck zur Berechnung des Durchschnitts:
- Berechnen Sie die Abweichung jedes Intervalls vom Mittelwert, was dem absoluten Wert der Differenz zwischen der Klassennote und dem Mittelwert entspricht.
- Multiplizieren Sie die Abweichung jedes Intervalls mit seiner absoluten Häufigkeit.
- Addieren Sie alle Ergebnisse aus dem vorherigen Schritt und dividieren Sie sie dann durch die Gesamtzahl der Daten. Das erhaltene Ergebnis ist die durchschnittliche Abweichung der in Intervalle gruppierten Stichprobe.
![]()
![]()
![]()
![]()
Zusammenfassend lautet die Formel zur Ermittlung der durchschnittlichen Abweichung aus gruppierten Daten :
![]()
Wenn Daten gruppiert werden, bedeutet dies normalerweise, dass viele Daten vorhanden sind und die Ermittlung der durchschnittlichen Abweichung viele Schritte erfordert. Daher werden für die Berechnung üblicherweise Häufigkeitstabellen verwendet.
Nachfolgend finden Sie eine Schritt-für-Schritt-Übung zur Berechnung der mittleren Abweichung, wenn Daten in Intervalle gruppiert werden:
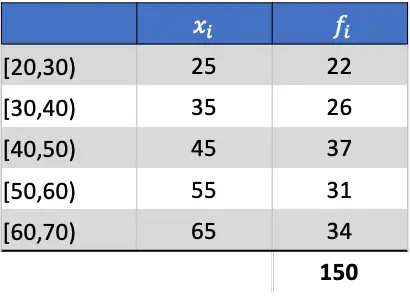
Als Erstes muss der Durchschnitt der gruppierten Daten berechnet werden. Dazu fügen wir der Tabelle eine Spalte hinzu, indem wir die Klassennotiz mit ihrer Häufigkeit multiplizieren:
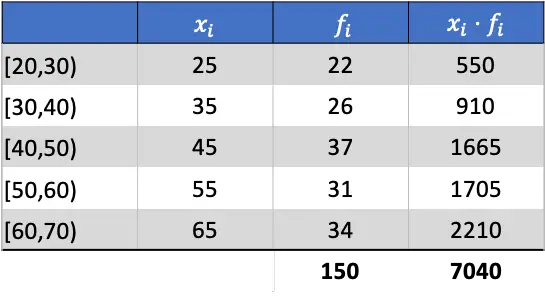
Das arithmetische Mittel ergibt sich daher aus der Division der Summe der hinzugefügten Spalte durch die Summe der absoluten Häufigkeiten:
![]()
Da wir nun den Mittelwert der Daten kennen, können wir alle notwendigen Spalten hinzufügen, um die mittlere Abweichung zu ermitteln:
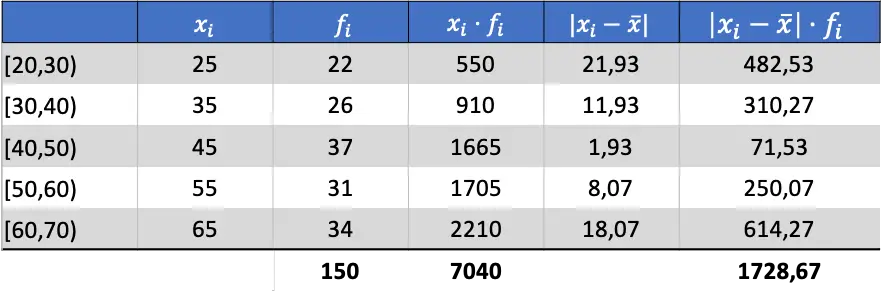
Um die durchschnittliche Abweichung zu erhalten, müssen Sie also die Summe der letzten Spalte durch die Gesamtzahl der Beobachtungen dividieren:
![]()