Quadratischer mittelwert

Hier erklären wir, was der quadratische Mittelwert ist und wie er berechnet wird. Darüber hinaus erfahren Sie die Vor- und Nachteile der Verwendung des Durchschnitts und eine Schritt-für-Schritt-Lösung. Schließlich können Sie mit dem Rechner am Ende des Artikels den quadratischen Mittelwert eines beliebigen Datensatzes berechnen.

Was ist das mittlere Quadrat?

Der quadratische Mittelwert ist ein Maß für die Zentralität der deskriptiven Statistik. Der quadratische Mittelwert ist gleich der Quadratwurzel des arithmetischen Mittels der Quadrate der Daten.

Der quadratische Mittelwert wird auch als quadratischer Mittelwert oder RMS bezeichnet.

Die Formel für den quadratischen Mittelwert lautet daher wie folgt:

Der quadratische Mittelwert ist besonders nützlich, wenn die statistische Variable positive und negative Werte annimmt, da durch die Quadrierung jedes Datenelements alle Werte positiv werden. Daher wird der mittlere Quadratwert zur Analyse von Variablen verwendet, bei denen nicht das Vorzeichen, sondern der Absolutwert wichtig ist.

Beispielsweise wird der mittlere Quadratwert zur Untersuchung von Messfehlern verwendet, da wir in diesen Fällen nicht darauf achten, ob der Fehler positiv oder negativ ist, sondern vielmehr die Größe des Fehlers bei der Messung analysieren.

Darüber hinaus haben die Quadrate großer Zahlen viel höhere Werte als die Quadrate kleiner Zahlen, sodass im mittleren Quadrat große Zahlen wichtiger sind als kleine Zahlen.

Der quadratische Mittelwert ist zusammen mit dem arithmetischen Mittel, dem gewichteten Mittel, dem geometrischen Mittel und dem harmonischen Mittel eine Art statistischer Durchschnitt.

Vor- und Nachteile des quadratischen Mittelwerts

Der quadratische Durchschnitt hat im Vergleich zu anderen Durchschnittsarten Vor- und Nachteile.

Der Hauptvorteil des quadratischen Mittelwerts besteht darin, dass Sie damit eine sehr gute Näherung für den Durchschnittswert einer diskreten Variablen erhalten. Andererseits besteht der große Nachteil des quadratischen Durchschnitts darin, dass seine Berechnung recht kompliziert ist, da mehrere Operationen durchgeführt werden müssen.

Im Gegensatz dazu ist der quadratische Mittelwert sehr nützlich für die Analyse von Fehlermessungen. Außerdem wird hohen Werten eine viel größere Bedeutung beigemessen, obwohl diese Eigenschaft impliziert, dass eine falsche Messung das Effektivwertergebnis erheblich verändert.

So berechnen Sie den quadratischen Mittelwert

Um den quadratischen Mittelwert zu berechnen, müssen folgende Schritte durchgeführt werden:

1. Berechnen Sie das Quadrat aller statistischen Daten.
2. Addieren Sie alle im vorherigen Schritt berechneten Quadrate.
3. Teilen Sie das Ergebnis durch die Anzahl der Datenelemente in der Stichprobe.
4. Finden Sie die Quadratwurzel des vorherigen Werts.
5. Das erhaltene Ergebnis ist der quadratische Mittelwert der statistischen Stichprobe.

👉 Mit dem Rechner unten können Sie den quadratischen Mittelwert eines beliebigen Datensatzes berechnen.

Beispiel für ein mittleres Quadrat

Sobald wir wissen, wie wir den quadratischen Mittelwert ermitteln, ermitteln wir als Beispiel den quadratischen Mittelwert einer Datenmenge.

• In einem Laborkurs an der Universität bittet der Professor seine Studenten, ein Experiment mit Chemikalien durchzuführen. Ziel des chemischen Experiments ist es, eine Lösung von insgesamt 3 Litern zu erhalten. Die Studierendengruppen erhielten folgende Daten:

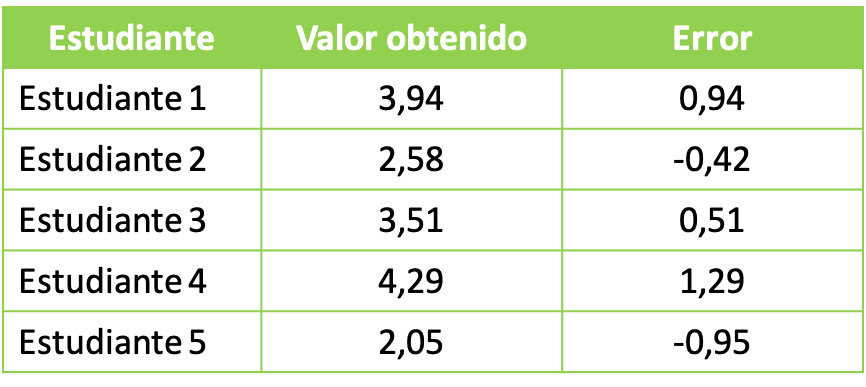
Um die erhaltenen statistischen Daten zu untersuchen, berechnen wir den Wert des quadratischen Mittelwerts mit dem von jeder Gruppe erhaltenen Fehler. Wir wenden daher die quadratische Mittelformel an:

Und wir setzen die Daten in die Formel ein und berechnen den quadratischen Mittelwert:

Somit beträgt der im Experiment erhaltene durchschnittliche Fehler gemäß dem quadratischen Mittelwert 0,88 Liter.

Mittlerer Quadratrechner

Geben Sie Daten aus einer beliebigen statistischen Stichprobe in den folgenden Rechner ein, um den quadratischen Mittelwert zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.