Mle für eine poisson-verteilung (schritt für schritt)

Die Maximum-Likelihood-Schätzung (MLE) ist eine Methode, mit der die Parameter einer bestimmten Verteilung geschätzt werden können.

In diesem Tutorial wird erläutert, wie der MLE für den Parameter λ einerPoisson-Verteilung berechnet wird.

Schritt 1: Schreiben Sie das PDF.

Schreiben Sie zunächst die Wahrscheinlichkeitsdichtefunktion der Poisson-Verteilung:

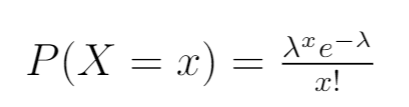
Schritt 2: Schreiben Sie die Wahrscheinlichkeitsfunktion.

Schreiben Sie als Nächstes die Wahrscheinlichkeitsfunktion. Dies ist einfach das Produkt der PDF für die beobachteten Werte x ₁ , …, x _n .

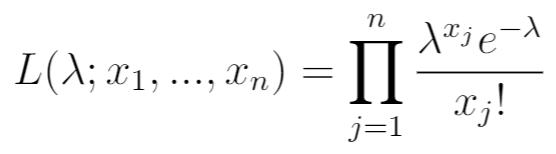
Schritt 3: Schreiben Sie die Wahrscheinlichkeitsfunktion des natürlichen Logarithmus.

Um die Berechnungen zu vereinfachen, können wir die natürliche Wahrscheinlichkeitsfunktion schreiben:

Schritt 4: Berechnen Sie die Ableitung der natürlichen Wahrscheinlichkeitsfunktion nach λ.

Dann können wir die Ableitung der natürlichen Wahrscheinlichkeitsfunktion nach dem Parameter λ berechnen:

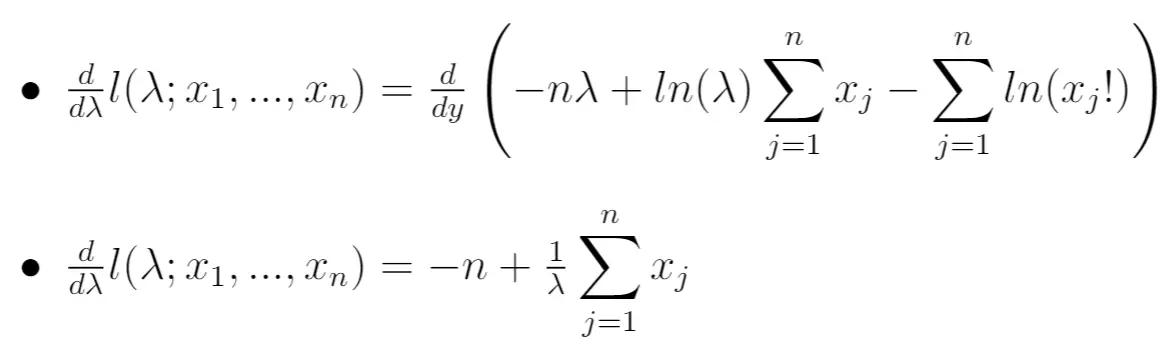
Schritt 5: Setzen Sie die Ableitung gleich Null und lösen Sie nach λ auf.

Schließlich setzen wir die Ableitung aus dem vorherigen Schritt gleich Null und lösen einfach nach λ auf:

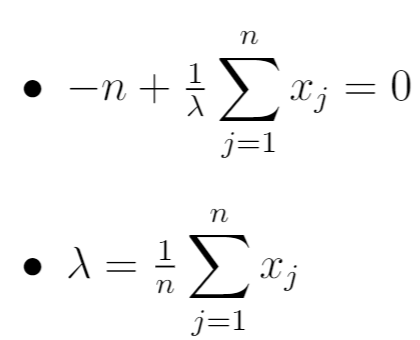
Somit ergibt sich für den MLE:

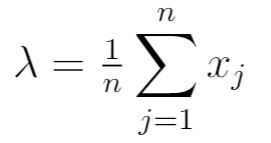
Dies entspricht dem Stichprobenmittelwert der n Beobachtungen in der Stichprobe.

Zusätzliche Ressourcen

Eine Einführung in die Poisson-Verteilung
Fischverteilungsrechner
So verwenden Sie die Poisson-Verteilung in Excel