Was ist eine eintönige beziehung? (definition + beispiele)

In der Statistik bezieht sich eine monotone Beziehung zwischen zwei Variablen auf ein Szenario, bei dem eine Änderung einer Variablen normalerweise mit einer Änderung einer anderen Variablen in eine bestimmte Richtung verbunden ist.

Es gibt zwei Arten monotoner Beziehungen:

Positiv monoton: Wenn der Wert einer Variablen steigt, nimmt tendenziell auch der Wert der anderen Variablen zu.

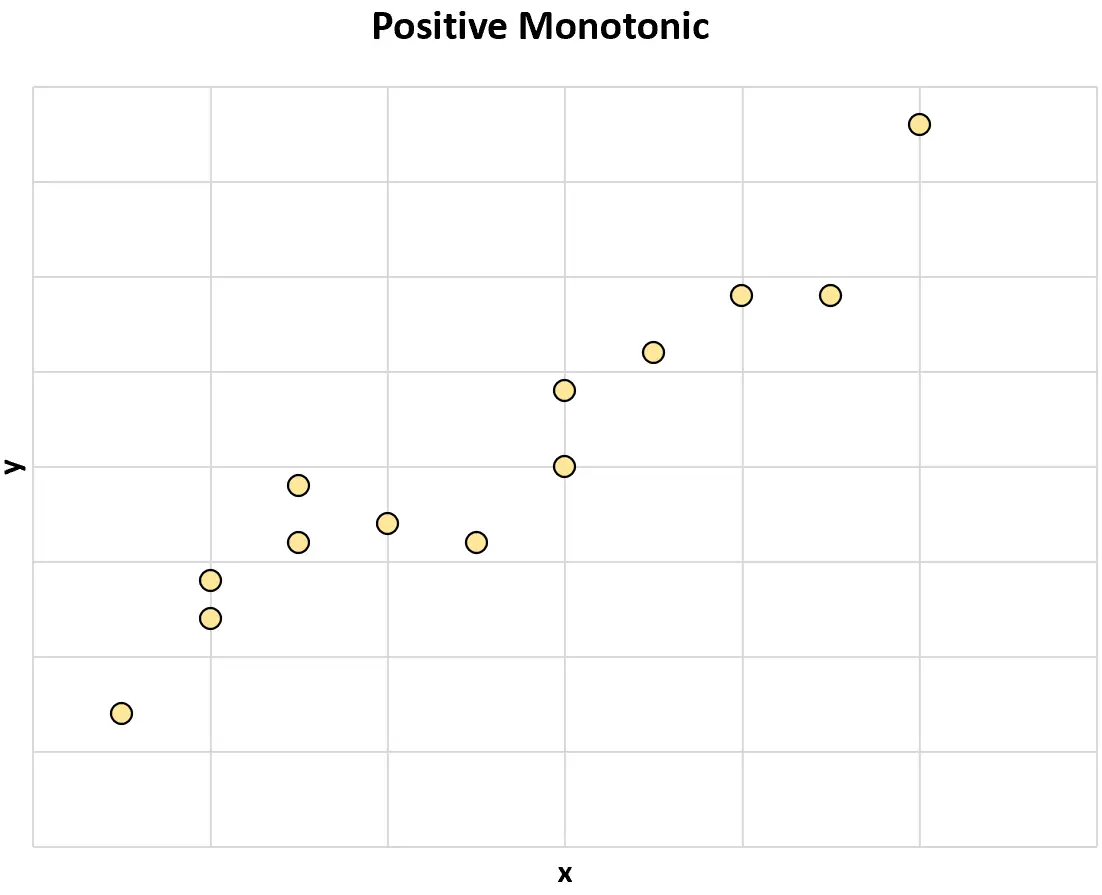
Negativ monoton: Wenn der Wert einer Variablen zunimmt, nimmt der Wert der anderen Variablen tendenziell ab.

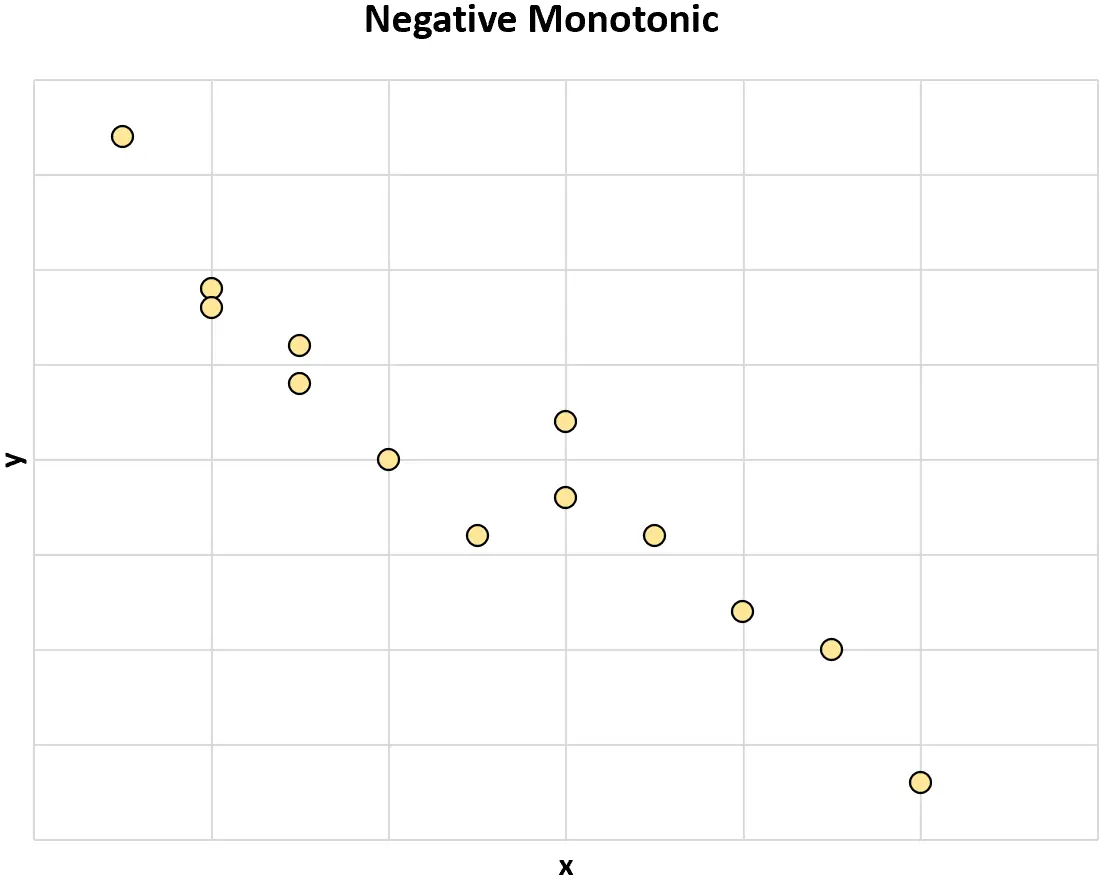
Wenn sich zwei Variablen im Allgemeinen nicht in die gleiche Richtung ändern, spricht man von einer nichtmonotonen Beziehung .

Hier ist ein Beispiel für eine nichtmonotone Beziehung zwischen zwei Variablen:

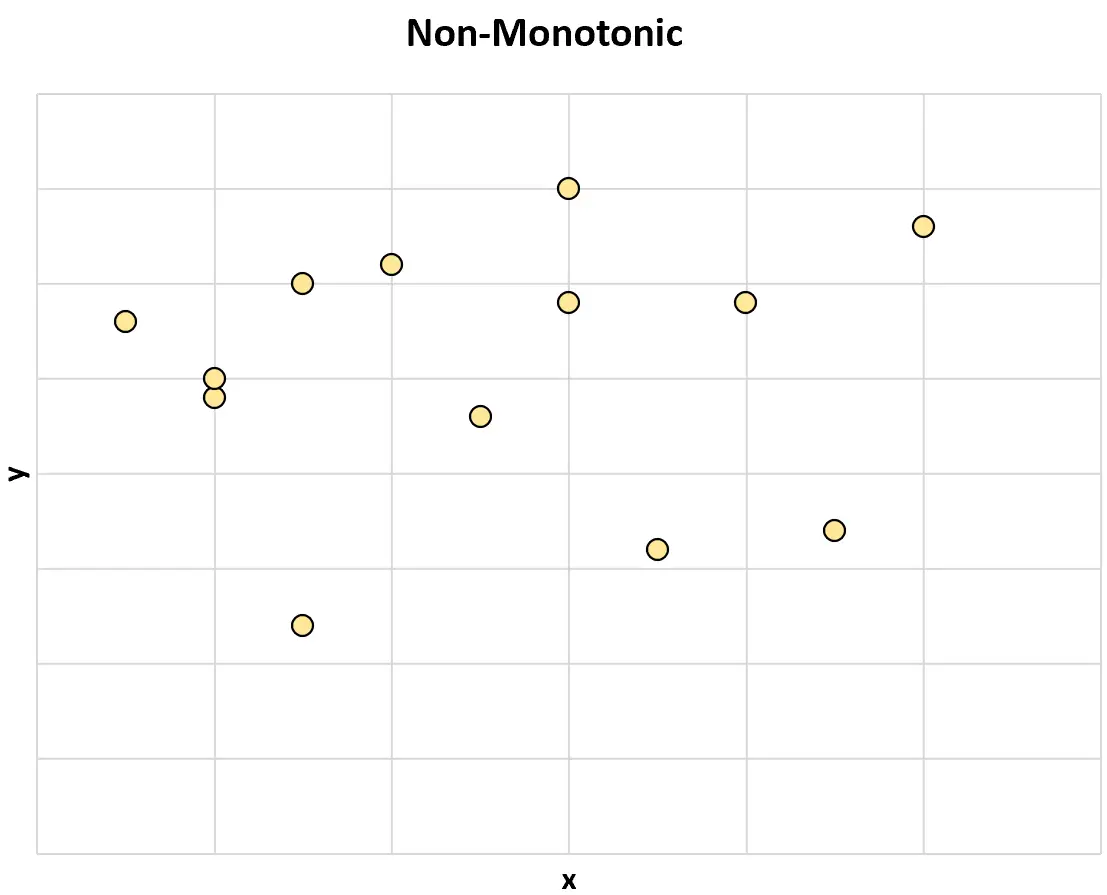
Und hier ist ein weiteres Beispiel für eine nichtmonotone Beziehung zwischen zwei Variablen:

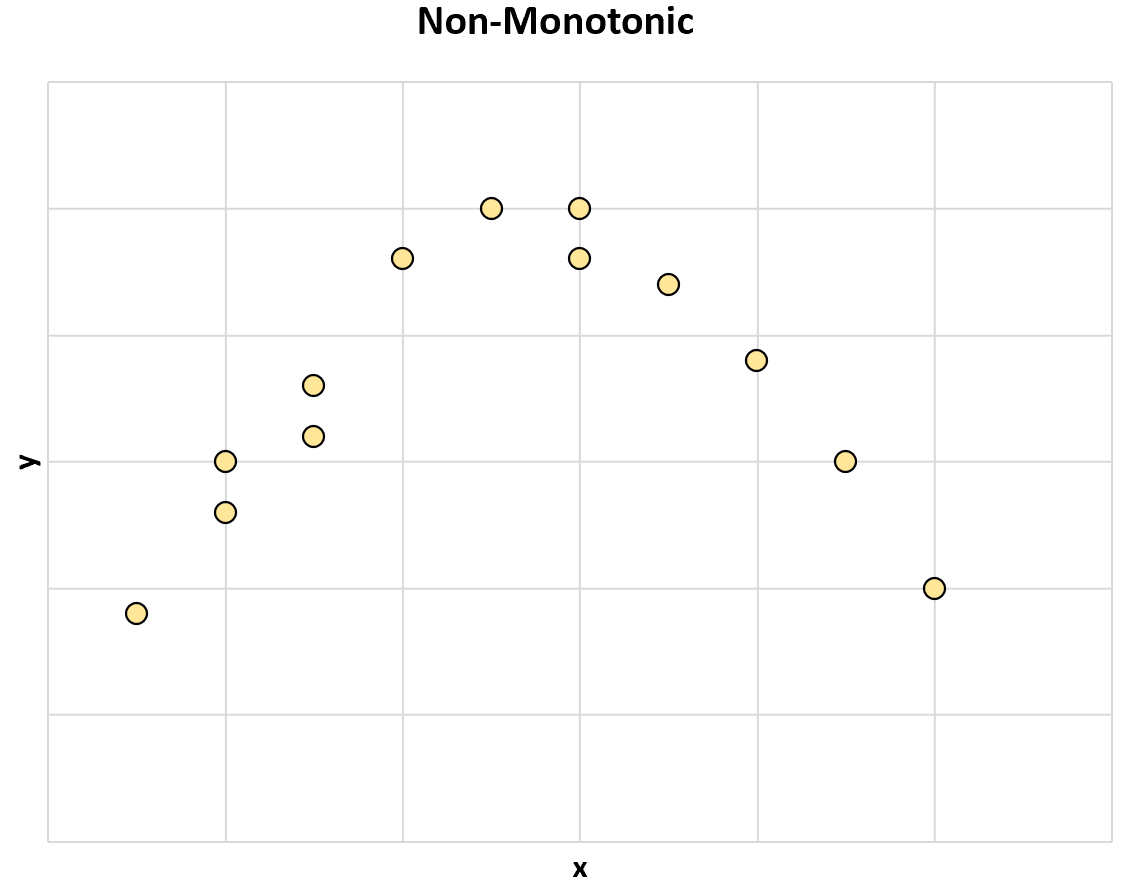
Wenn der Wert von x zunimmt, erhöht sich manchmal der Wert von y, manchmal nimmt der Wert von y jedoch ab .

Streng eintönig oder nicht streng eintönig

Von einem strikt monotonen Zusammenhang zwischen zwei Variablen spricht man, wenn Änderungen einer Variablen immer mit einer gleichsinnigen Änderung einer anderen Variablen einhergehen.

Die folgende Grafik veranschaulicht beispielsweise eine streng positive monotone Beziehung zwischen zwei Variablen:

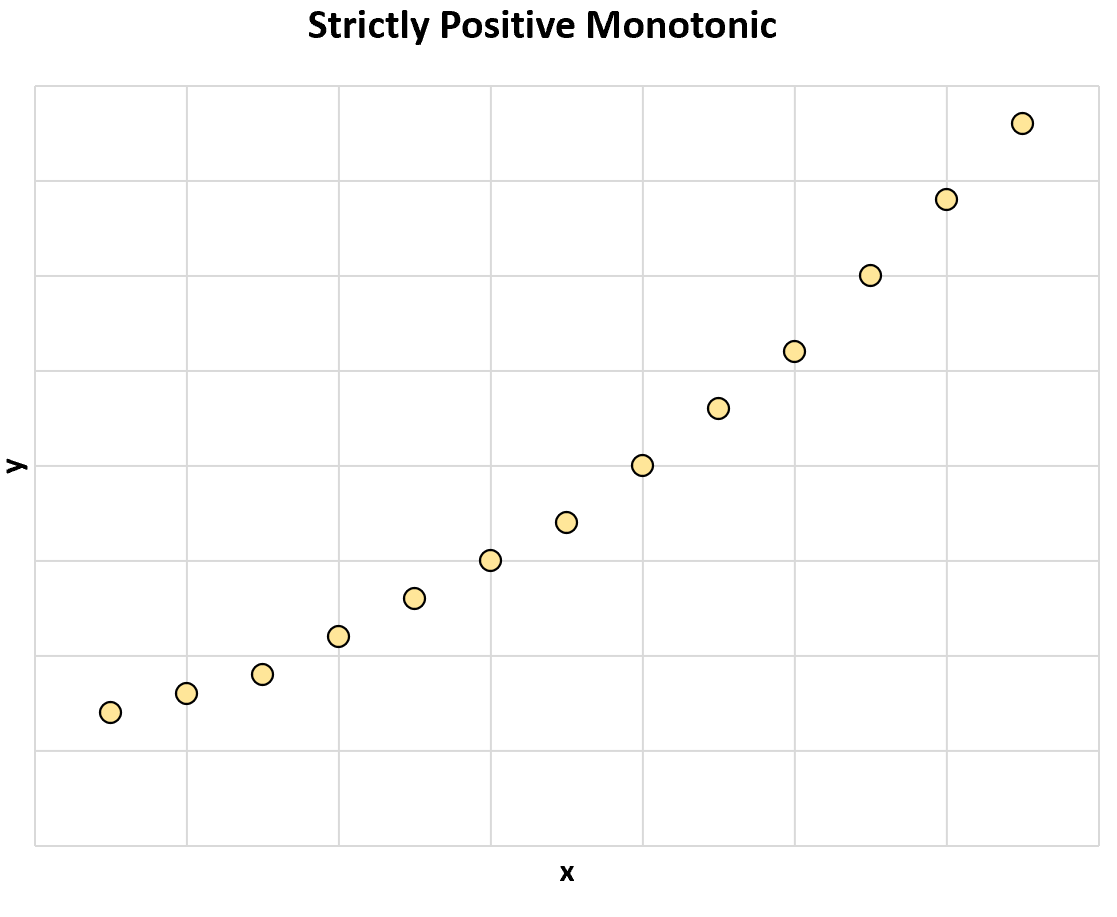
Wenn der Wert von x zunimmt, nimmt auch der Wert von y immer zu.

Die folgende Grafik veranschaulicht eine streng negative monotone Beziehung zwischen zwei Variablen:

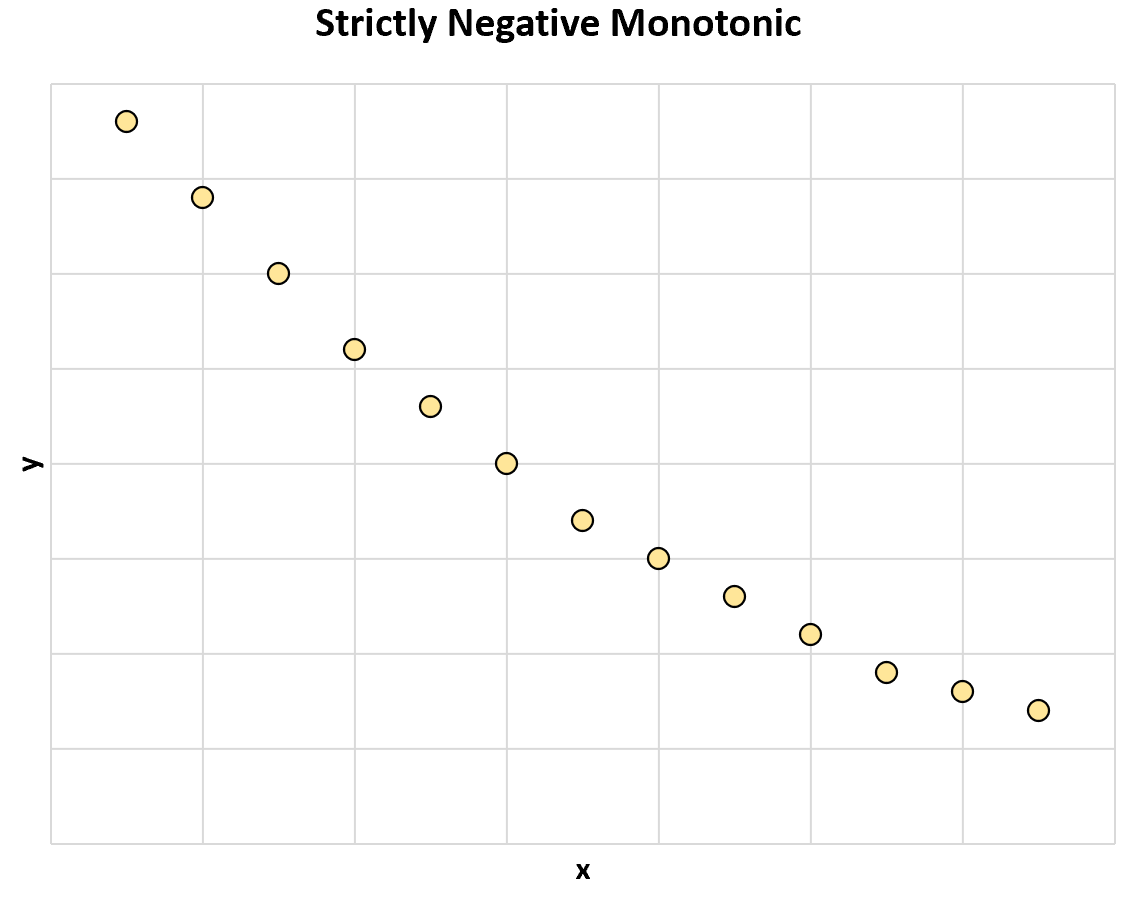
Wenn der Wert von x zunimmt, nimmt der Wert von y immer ab.

Wie man monotone Beziehungen quantifiziert

Die gebräuchlichste Methode zur Quantifizierung der Beziehung zwischen zwei Variablen ist die Verwendung des Pearson-Korrelationskoeffizienten , der den linearen Zusammenhang zwischen zwei Variablen misst.

Dieser Koeffizient nimmt immer einen Wert zwischen -1 und 1 an, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Je näher der Koeffizient bei 1 liegt, desto stärker ist die positive Beziehung zwischen zwei Variablen. Umgekehrt gilt: Je näher der Koeffizient bei -1 liegt, desto stärker ist die negative Beziehung zwischen zwei Variablen.

Wenn die Beziehung zwischen zwei Variablen jedoch monoton, aber nicht linear ist (wie eine exponentielle Beziehung), ist es eine gute Idee, die Spearman-Rank-Korrelation zu verwenden, die für die gute Verarbeitung monotoner Beziehungen entwickelt wurde.

Unabhängig davon, welche Art von Korrelationskoeffizient Sie berechnen, ist es immer eine gute Idee, ein Streudiagramm zu erstellen, um auch die Beziehung zwischen Variablen zu visualisieren.