Das monty-hall-problem: eine einfache visuelle erklärung

In einer alten Spielshow mit dem Titel „Let’s Make a Deal“ überreichte Moderator Monty Hall den Teilnehmern drei Türen.

Eine der Türen enthielt einen Preis, die anderen beiden nicht.

Monty würde den Teilnehmer bitten, auszuwählen, welche Tür seiner Meinung nach den Preis enthielt.

Sobald der Teilnehmer eine Tür ausgewählt hatte, öffnete Monty eine Tür, die den Preis nicht enthielt .

Der Preis blieb in einer der beiden verschlossenen Türen.

Monty würde den Kandidaten dann fragen, ob er die Tür wechseln wolle.

Auch wenn es kaum zu glauben scheint, stellt sich heraus, dass ein Türwechsel zu diesem Zeitpunkt des Spiels tatsächlich eine größere Gewinnchance bietet.

Lesen Sie weiter, um herauszufinden, warum!

Das Monty-Hall-Problem visuell erklärt

Um zu veranschaulichen, warum ein Türwechsel zu einer höheren Gewinnwahrscheinlichkeit führt, betrachten Sie die folgenden Szenarien, in denen Sie zuerst Tür 1 auswählen.

Szenario 1: Sie wählen Tür 1 und der Preis befindet sich tatsächlich hinter Tür 1.

In diesem Fall öffnet Monty Tür 2 oder 3 und zeigt Ihnen, dass sich hinter keiner Tür etwas befindet. Wer bei Tür 1 bleibt, gewinnt .

Szenario 2: Sie wählen Tür 1 und der Preis befindet sich tatsächlich hinter Tür 2.

In diesem Fall muss Monty Tür 3 öffnen und dir zeigen, dass sich dahinter nichts befindet. Wenn Sie bei Tür 1 bleiben, verlieren Sie .

Szenario 3: Sie wählen Tür 1 und der Preis befindet sich tatsächlich hinter Tür 3.

In diesem Fall muss Monty Tür 2 öffnen und dir zeigen, dass sich dahinter nichts befindet. Wenn Sie bei Tür 1 bleiben, verlieren Sie .

Dies sind alles mögliche Ergebnisse, wenn Sie sich für Tür 1 entscheiden. Beachten Sie, dass Sie nur ein Drittel der Zeit sparen, wenn Sie bei Tür 1 bleiben. Aber wenn Sie wechseln, sparen Sie zwei Drittel der Zeit.

Die folgende Tabelle fasst alle möglichen Szenarien dieser Spielshow sowie die mit der Wartung und Änderung verbundenen Ergebnisse zusammen:

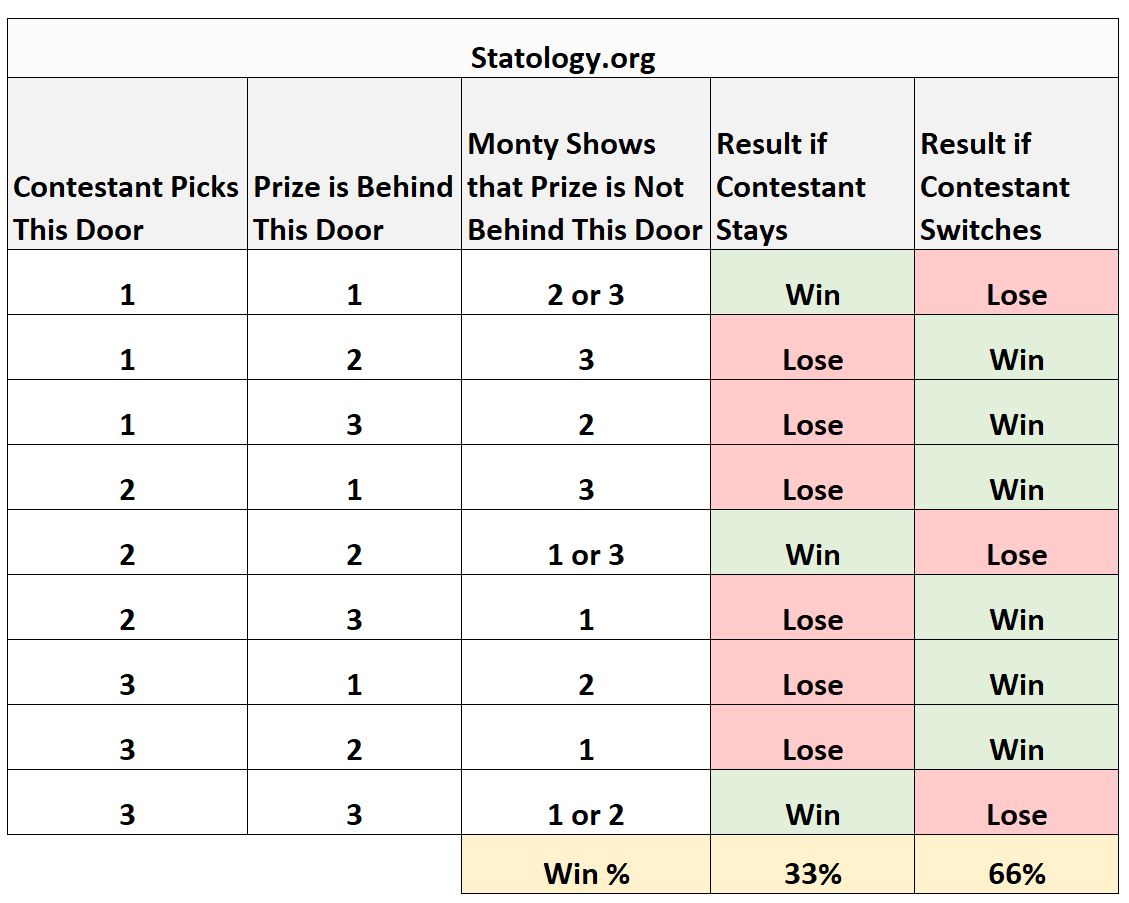
Aus der Tabelle können wir ersehen, dass Sie in 33 % der Fälle gewinnen, wenn Sie bleiben, aber in 66 % der Fälle, wenn Sie wechseln.

Ein Türwechsel erhöht also die Wahrscheinlichkeit, dass Sie den Preis gewinnen.

Obwohl dies intuitiv vielleicht keinen Sinn ergibt, lügt die Mathematik nicht.