Was ist morans selbst? (definition & #038; beispiel)

Morans I ist eine Methode zur Messung der räumlichen Autokorrelation.

Einfach ausgedrückt ist es eine Möglichkeit, zu quantifizieren, wie eng Werte im 2D-Raum geclustert sind. Es wird häufig in der Geographie und der geografischen Informationswissenschaft (GIS) verwendet, um zu messen, wie eng verschiedene Merkmale auf einer Karte gruppiert sind, z. B. Haushaltseinkommen, Bildungsniveau usw.

Morans Ich: die Formel

Die Formel zur Berechnung von Morans I lautet:

I = (N/W)*ΣΣw _ij (x _i – x )(x _j – x )/Σ(x _i – x ) ²

Gold:

• N: Die Anzahl der durch i und j indizierten räumlichen Einheiten
• W: Die Summe aller w _ij
• x: Die interessierende Variable (Haushaltseinkommen, Schuljahre usw.)
• x : Der Durchschnitt von x
• w _ij : Eine Matrix räumlicher Gewichte

Sie müssen dieses Maß wahrscheinlich nie von Hand berechnen, da die meisten Statistikprogramme es für Sie berechnen können, aber es ist hilfreich, die zugrunde liegende Formel zu kennen.

Der Wert von Morans I kann zwischen -1 und 1 liegen, wobei:

• -1: Die interessierende Variable ist perfekt verteilt
• 0: Die interessierende Variable ist zufällig verteilt
• 1: Die interessierende Variable ist perfekt gruppiert

Neben der Berechnung von Moran’s I berechnen die meisten Statistikprogramme auch einen entsprechenden p-Wert, der verwendet werden kann, um zu bestimmen, ob die Daten zufällig verteilt sind oder nicht.

Der Moran-Test verwendet die folgenden Null- und Alternativhypothesen:

Nullhypothese (H ₀ ): Die Daten sind zufällig verteilt.

Alternativhypothese ( _HA ): Daten sind nicht zufällig verteilt, das heißt, sie sind in sichtbaren Mustern gruppiert.

Wenn der p-Wert, der Morans I entspricht, unter einem bestimmten Signifikanzniveau liegt (d. h. α = 0,05), können wir die Nullhypothese ablehnen und daraus schließen, dass die Daten räumlich geclustert sind, sodass es unwahrscheinlich ist, dass sie räumlich geclustert werden. geschah zufällig.

Morans I: einige Beispiele

Die folgenden Beispiele stellen falsche Karten mit unterschiedlichen Werten für Morans I dar.

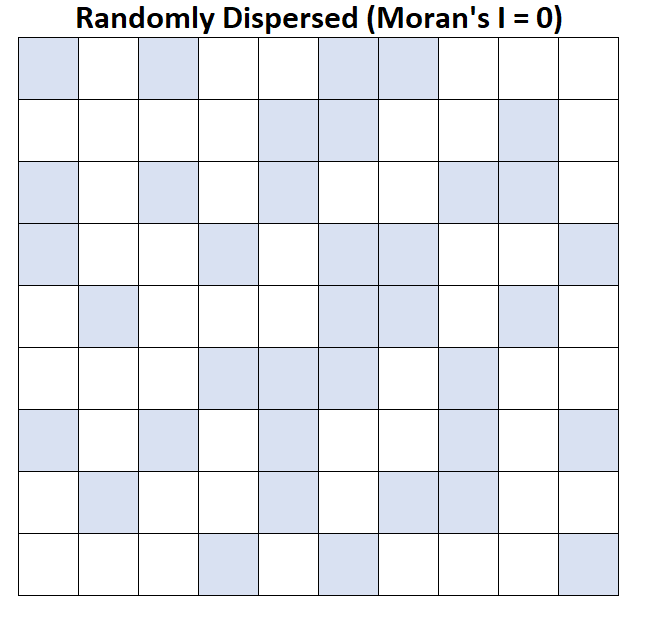
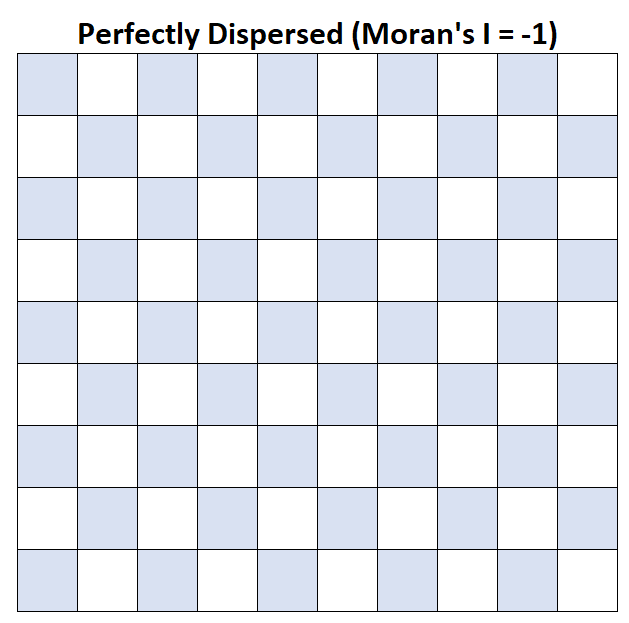
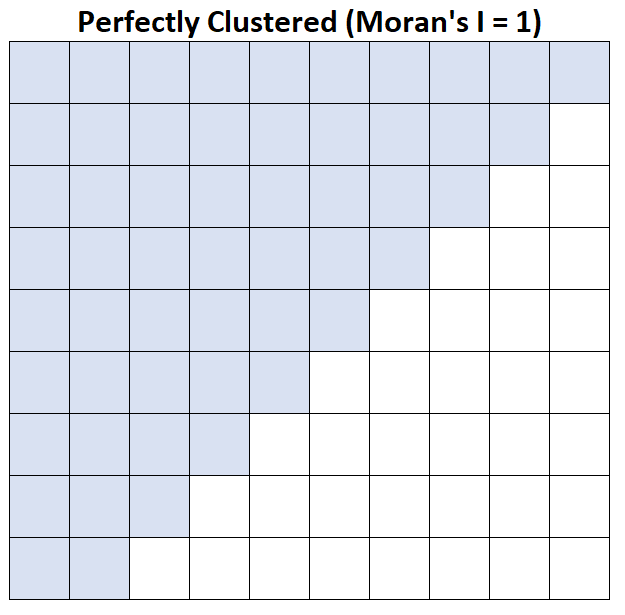
Nehmen wir an, dass jedes Quadrat auf der Karte einen Landkreis darstellt und dass Landkreise mit einem durchschnittlichen Haushaltseinkommen über 50.000 US-Dollar blau angezeigt werden.

Morans I = 0: Das durchschnittliche Haushaltseinkommen ist zufällig verteilt (dh zufällige Cluster in zufälligen Gebieten).

Morans I = -1: Das durchschnittliche Haushaltseinkommen ist perfekt gestreut.

Morans I = 1: Das durchschnittliche Haushaltseinkommen ist perfekt gruppiert.

In diesem Beispiel finden Sie ein konkretes Beispiel für die Berechnung von Morans I in der Statistiksoftware R.