So testen sie die multikollinearität in stata

Multikollinearität in der Regressionsanalyse tritt auf, wenn zwei oder mehr erklärende Variablen stark miteinander korrelieren, sodass sie im Regressionsmodell keine eindeutigen oder unabhängigen Informationen liefern. Wenn der Korrelationsgrad zwischen den Variablen hoch genug ist, kann dies zu Problemen bei der Anpassung und Interpretation des Regressionsmodells führen.

Angenommen, Sie führen eine multiple lineare Regression mit den folgenden Variablen durch:

Variable Reaktion: maximaler vertikaler Sprung

Erklärende Variablen: Schuhgröße, Körpergröße, Übungszeit

In diesem Fall besteht wahrscheinlich ein starker Zusammenhang zwischen den erklärenden Variablen Schuhgröße und -größe, da große Menschen tendenziell größere Schuhgrößen haben. Dies bedeutet, dass Multikollinearität bei dieser Regression wahrscheinlich ein Problem darstellt.

Glücklicherweise ist es möglich, Multikollinearität mithilfe einer Metrik namens Varianzinflationsfaktor (VIF) zu erkennen, die die Korrelation und Stärke der Korrelation zwischen erklärenden Variablen in einem Regressionsmodell misst.

In diesem Tutorial wird erläutert, wie Sie mit VIF Multikollinearität in einer Regressionsanalyse in Stata erkennen.

Beispiel: Multikollinearität in Stata

Für dieses Beispiel verwenden wir den integrierten Datensatz von Stata namens auto . Verwenden Sie den folgenden Befehl, um den Datensatz zu laden:

automatisch verwenden

Wir werden den Befehl regress verwenden, um ein multiples lineares Regressionsmodell anzupassen, wobei wir den Preis als Antwortvariable und Gewicht, Länge und mpg als erklärende Variablen verwenden:

Regression Preis Gewicht Länge mpg

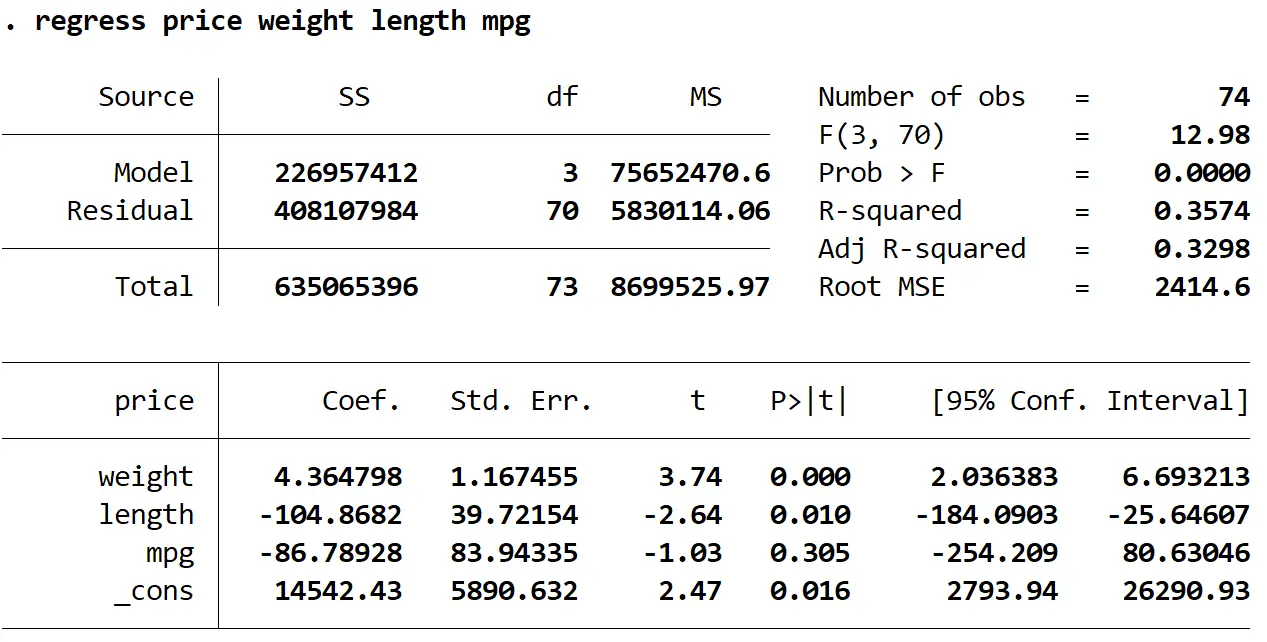
Als nächstes verwenden wir den Befehl vive , um die Multikollinearität zu testen:

lebhaft

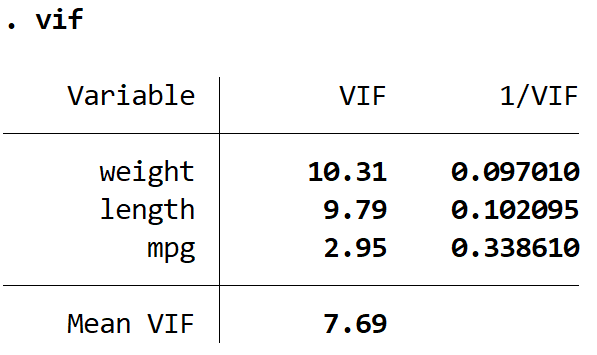
Dies erzeugt einen VIF-Wert für jede der erklärenden Variablen im Modell. Der VIF-Wert beginnt bei 1 und hat keine Obergrenze. Eine allgemeine Regel für die Interpretation von VIFs lautet:

• Ein Wert von 1 gibt an, dass keine Korrelation zwischen einer bestimmten erklärenden Variablen und einer anderen erklärenden Variablen im Modell besteht.
• Ein Wert zwischen 1 und 5 weist auf eine mäßige Korrelation zwischen einer bestimmten erklärenden Variablen und anderen erklärenden Variablen im Modell hin, ist jedoch oft nicht schwerwiegend genug, um besondere Aufmerksamkeit zu erfordern.
• Ein Wert größer als 5 weist auf eine potenziell schwerwiegende Korrelation zwischen einer bestimmten erklärenden Variablen und anderen erklärenden Variablen im Modell hin. In diesem Fall sind die Koeffizientenschätzungen und p-Werte in den Regressionsergebnissen wahrscheinlich unzuverlässig.

Wir können sehen, dass die VIF-Werte für Gewicht und Länge größer als 5 sind, was darauf hindeutet, dass Multikollinearität wahrscheinlich ein Problem im Regressionsmodell darstellt.

Wie man mit Multikollinearität umgeht

Der einfachste Weg, mit Multikollinearität umzugehen, besteht häufig darin, einfach eine der Problemvariablen zu entfernen, da die Variable, die Sie entfernen, wahrscheinlich ohnehin redundant ist und dem Modell nur wenige eindeutige oder unabhängige Informationen hinzufügt.

Um zu bestimmen, welche Variable entfernt werden soll, können wir mit dem Befehl corr eine Korrelationsmatrix erstellen, um die Korrelationskoeffizienten zwischen den einzelnen Variablen im Modell anzuzeigen. Dies kann uns dabei helfen, zu identifizieren, welche Variablen möglicherweise stark miteinander korrelieren und das Problem verursachen könnten Problem der Multikollinearität:

Korr. Preis Gewicht Länge mpg

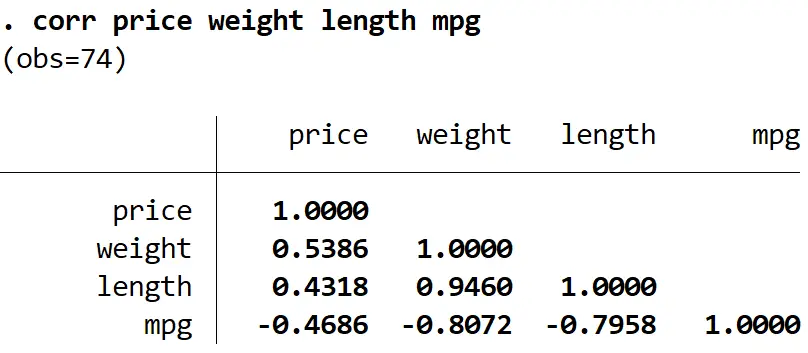
Wir können sehen, dass die Länge stark mit Gewicht und mpg korreliert und die geringste Korrelation mit der Antwortvariablen „Preis“ aufweist. Somit könnte das Entfernen der Modelllänge das Multikollinearitätsproblem lösen, ohne die Gesamtqualität des Regressionsmodells zu beeinträchtigen.

Um dies zu testen, können wir die Regressionsanalyse erneut ausführen und dabei nur Gewicht und mpg als erklärende Variablen verwenden:

Regressionspreis Gewicht mpg

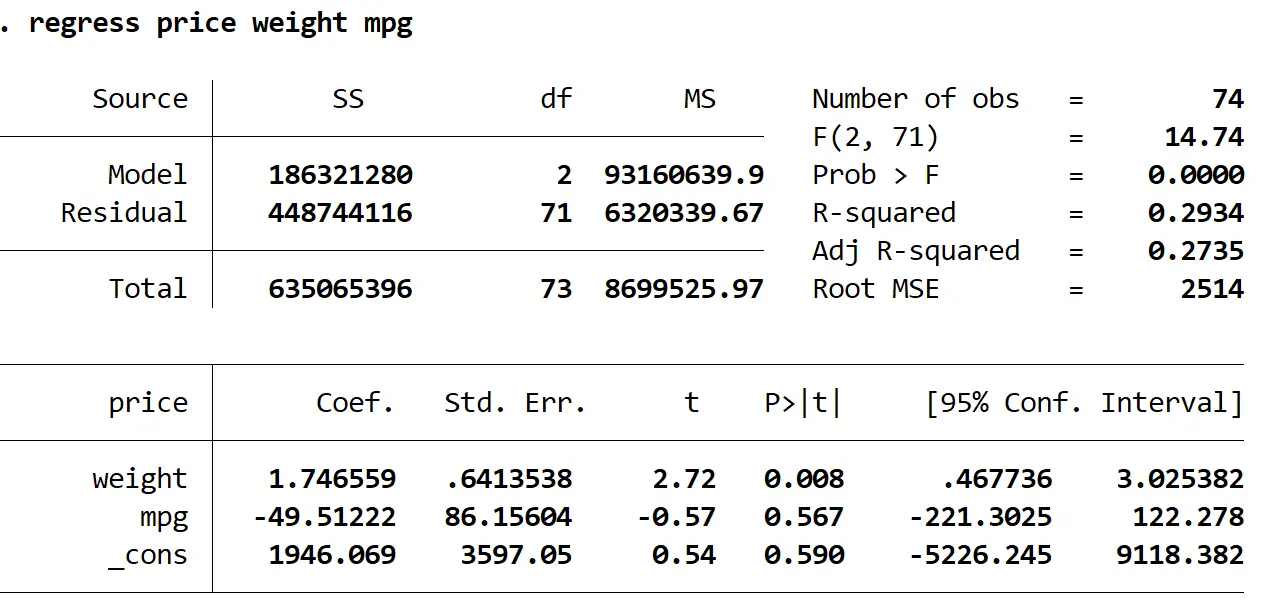
Wir können sehen, dass das angepasste R-Quadrat dieses Modells 0,2735 beträgt, verglichen mit 0,3298 im Vorgängermodell. Dies deutet darauf hin, dass der Gesamtnutzen des Modells nur geringfügig abgenommen hat. Dann können wir die VIF-Werte mit dem VIF- Befehl ermitteln:

LEBHAFT

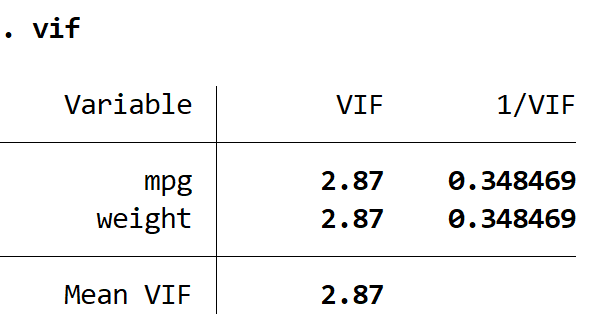
Beide VIF-Werte liegen unter 5, was darauf hinweist, dass Multikollinearität im Modell kein Problem mehr darstellt.