Was ist ein multinomialtest? (definition & #038; beispiel)

Ein multinomialer Test wird verwendet, um zu bestimmen, ob eine kategoriale Variable einer hypothetischen Verteilung folgt.

Dieser Test verwendet die folgenden Null- und Alternativhypothesen :

H ₀ : Eine kategoriale Variable folgt einer hypothetischen Verteilung.

H _A : Eine kategoriale Variable folgt nicht der hypothetischen Verteilung.

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), können wir die Nullhypothese ablehnen und daraus schließen, dass die Variable nicht der hypothetischen Verteilung folgt.

Dieser Test wird verwendet, wenn eine Variable k verschiedene Ergebnisse annehmen kann. Ein klassisches Beispiel für einen Multinomialtest ist der Test, bei dem wir feststellen wollen, ob bestimmte Würfel fair sind. Wenn Sie einen Würfel werfen, beträgt die Wahrscheinlichkeit, dass er auf jede Zahl (1 bis 6) fällt, 1/6.

Um zu testen, ob ein Würfel fair ist, können wir ihn mehrmals würfeln und prüfen, ob die Häufigkeit, mit der er auf verschiedenen Zahlen landet, deutlich von dem abweicht, was wir erwarten würden.

Die folgenden Beispiele zeigen, wie ein multinomialer Test mit der statistischen Programmiersprache R durchgeführt wird.

Beispiel 1: Faire Würfel

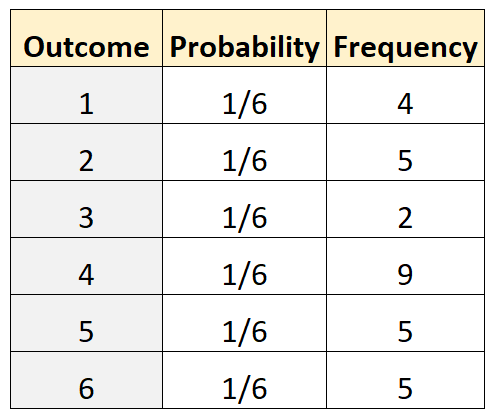
Angenommen, wir möchten feststellen, ob ein Würfel fair ist. Um dies zu testen, führen wir es 30 Mal durch und zeichnen die Häufigkeit jedes Ergebnisses auf. Die folgende Tabelle zeigt die Ergebnisse:

Der folgende Code in R kann verwendet werden, um einen Multinomialtest durchzuführen:

 library (EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    324632 0 0.4306

Der p-Wert des Tests beträgt 0,4306 . Da dieser p-Wert nicht kleiner als 0,05 ist, werden wir die Nullhypothese nicht ablehnen. Wir haben also nicht genügend Beweise, um zu sagen, dass die Würfel unfair sind.

Beispiel 2: Produktverkäufe

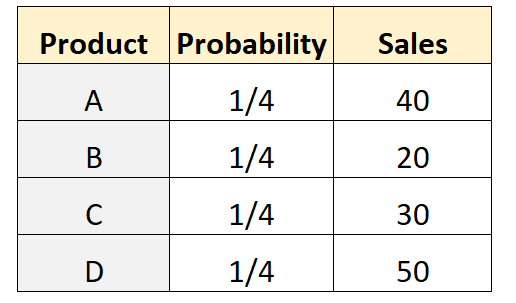
Angenommen, ein Ladenbesitzer geht davon aus, dass eine gleiche Anzahl von Kunden jedes der vier verschiedenen Produkte kaufen wird. Um dies zu testen, wird die Anzahl der Kunden erfasst, die jedes Produkt in einer bestimmten Woche gekauft haben. Die folgende Tabelle zeigt die Ergebnisse:

Der folgende Code in R kann verwendet werden, um einen multinomialen Test für diesen Datensatz durchzuführen:

 library (EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    477191 0 0.00226

Der p-Wert des Tests beträgt 0,00226 . Da dieser p-Wert kleiner als 0,05 ist, lehnen wir die Nullhypothese ab. Wir haben also genügend Beweise dafür, dass die Umsätze nicht bei jedem Produkt gleich sind.

Beispiel 3: Murmeln in einer Tüte

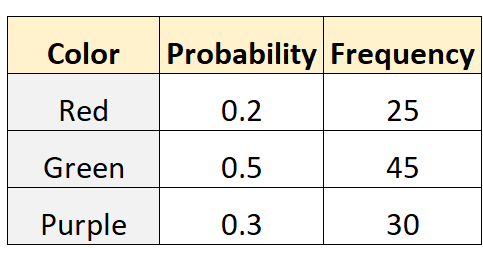
Tom gibt an, dass die Wahrscheinlichkeit, eine rote, grüne oder violette Murmel aus einem Beutel auszuwählen, jeweils 0,2, 0,5 und 0,3 beträgt. Um dies zu testen, greift sein Freund Mike 100 Mal in die Tasche und holt eine Murmel (mit Ersatz) heraus. Die folgende Tabelle zeigt die Ergebnisse:

Der folgende Code in R kann verwendet werden, um einen multinomialen Test für diesen Datensatz durchzuführen:

 library (EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
      5151 0.0037 0.3999

Der p-Wert des Tests beträgt 0,3999 . Da dieser p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Wir haben daher nicht genügend Beweise, um sagen zu können, dass sich die Verteilung der Murmeln im Beutel von der von Tom angegebenen unterscheidet.

Zusätzliche Ressourcen

Eine Einführung in die Multinomialverteilung
Multinomialverteilungsrechner