Eine einführung in die multinomialverteilung

Die Multinomialverteilung beschreibt die Wahrscheinlichkeit, eine bestimmte Anzahl von Zählungen für k verschiedene Ergebnisse zu erhalten, wenn jedes Ergebnis eine feste Eintrittswahrscheinlichkeit hat.

_{Wenn eine} Zufallsvariable _{_} mit der folgenden Formel gefunden werden kann:

Wahrscheinlichkeit = n! * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

Gold:

• n: Gesamtzahl der Ereignisse
• x ₁ : Häufigkeit, mit der Ergebnis 1 auftritt
• p ₁ : Wahrscheinlichkeit, dass Ergebnis 1 in einem bestimmten Versuch auftritt

Angenommen, in einer Urne befinden sich 5 rote Murmeln, 3 grüne Murmeln und 2 blaue Murmeln. Wenn wir zufällig 5 Murmeln aus der Urne ziehen und ersetzen, wie groß ist die Wahrscheinlichkeit, genau 2 rote Murmeln, 2 grüne Murmeln und 1 blaue Murmel zu erhalten?

Um diese Frage zu beantworten, können wir die Multinomialverteilung mit den folgenden Parametern verwenden:

• n : 5
• x ₁ (# rote Murmeln) = 2, x ₂ (# grüne Murmeln) = 2, x ₃ (# blaue Murmeln) = 1
• p ₁ (rote Wahrscheinlichkeit) = 0,5, p ₂ (grüne Wahrscheinlichkeit) = 0,3, p ₃ (blaue Wahrscheinlichkeit) = 0,2

Wenn wir diese Zahlen in die Formel einsetzen, erhalten wir folgende Wahrscheinlichkeit:

Wahrscheinlichkeit = 5! * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0,135 .

Probleme der multinomialen Verteilungspraxis

Nutzen Sie die folgenden Übungsaufgaben, um Ihr Wissen über die Multinomialverteilung zu testen.

Hinweis: Wir werden den Multinomialverteilungsrechner verwenden, um die Antworten auf diese Fragen zu berechnen.

Problem 1

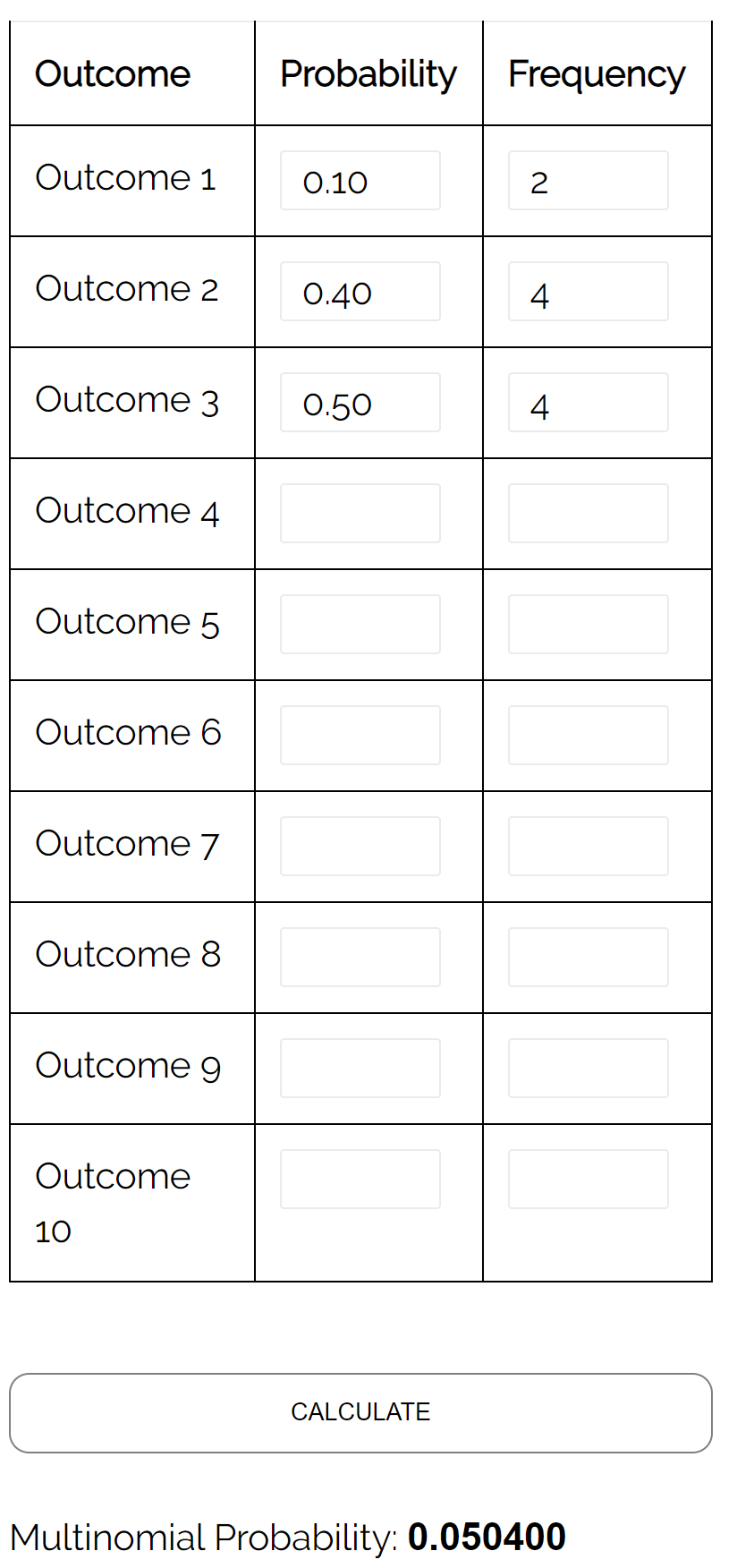
Frage: Bei einer Dreierwahl zum Bürgermeister erhält Kandidat A 10 % der Stimmen, Kandidat B 40 % der Stimmen und Kandidat C 50 % der Stimmen. Wenn wir eine Zufallsstichprobe von 10 Wählern auswählen, wie groß ist die Wahrscheinlichkeit, dass 2 für Kandidat A, 4 für Kandidat B und 4 für Kandidat C gestimmt haben?

Antwort: Wenn wir den Multinomialverteilungsrechner mit den folgenden Eingaben verwenden, ermitteln wir, dass die Wahrscheinlichkeit 0,0504 beträgt:

Problem 2

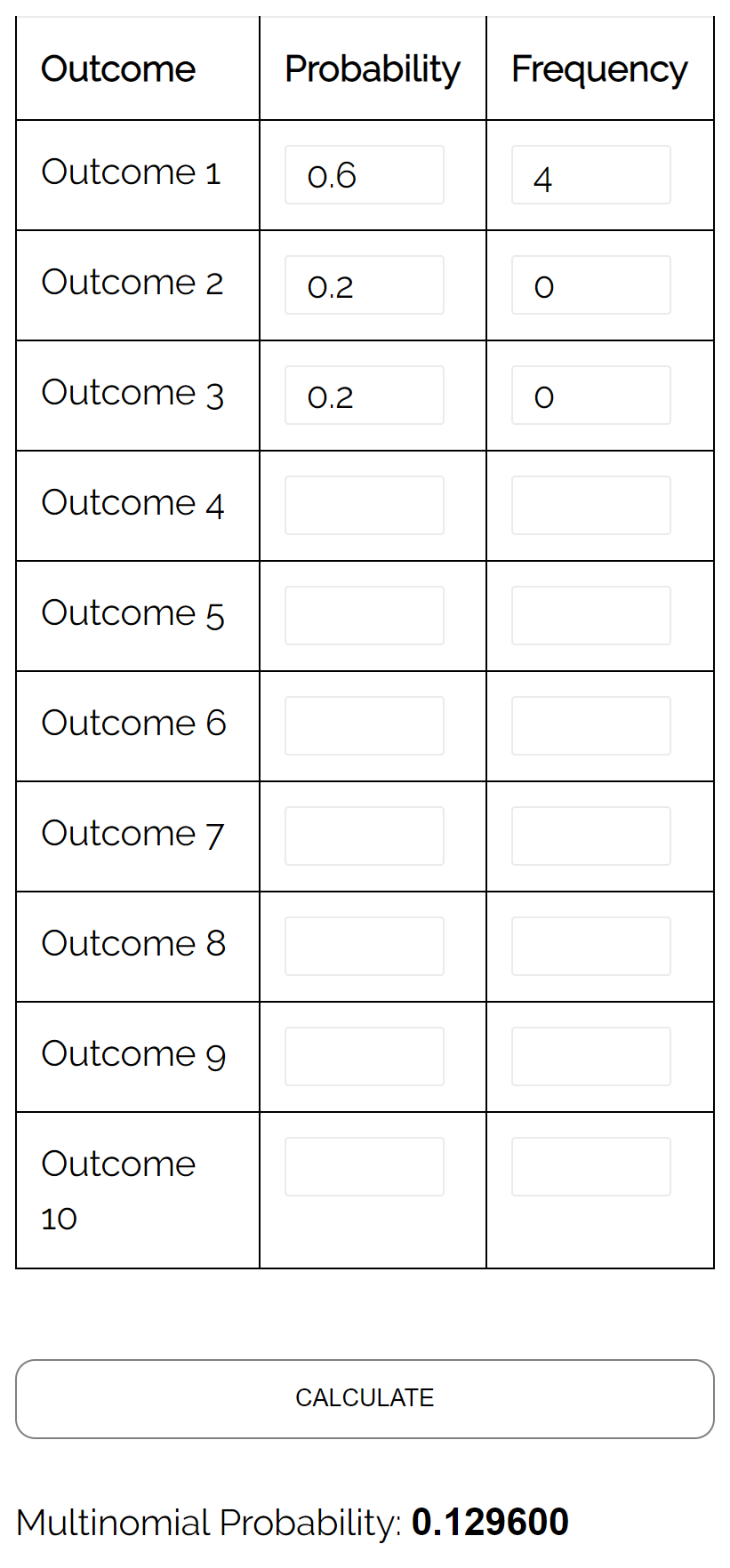
Frage: Angenommen, eine Urne enthält 6 gelbe Murmeln, 2 rote Murmeln und 2 rosa Murmeln. Wenn wir zufällig 4 Kugeln aus der Urne auswählen und sie ersetzen, wie groß ist die Wahrscheinlichkeit, dass alle 4 Kugeln gelb sind?

Antwort: Wenn wir den Multinomialverteilungsrechner mit den folgenden Eingaben verwenden, ermitteln wir, dass die Wahrscheinlichkeit 0,1296 beträgt:

Problem 3

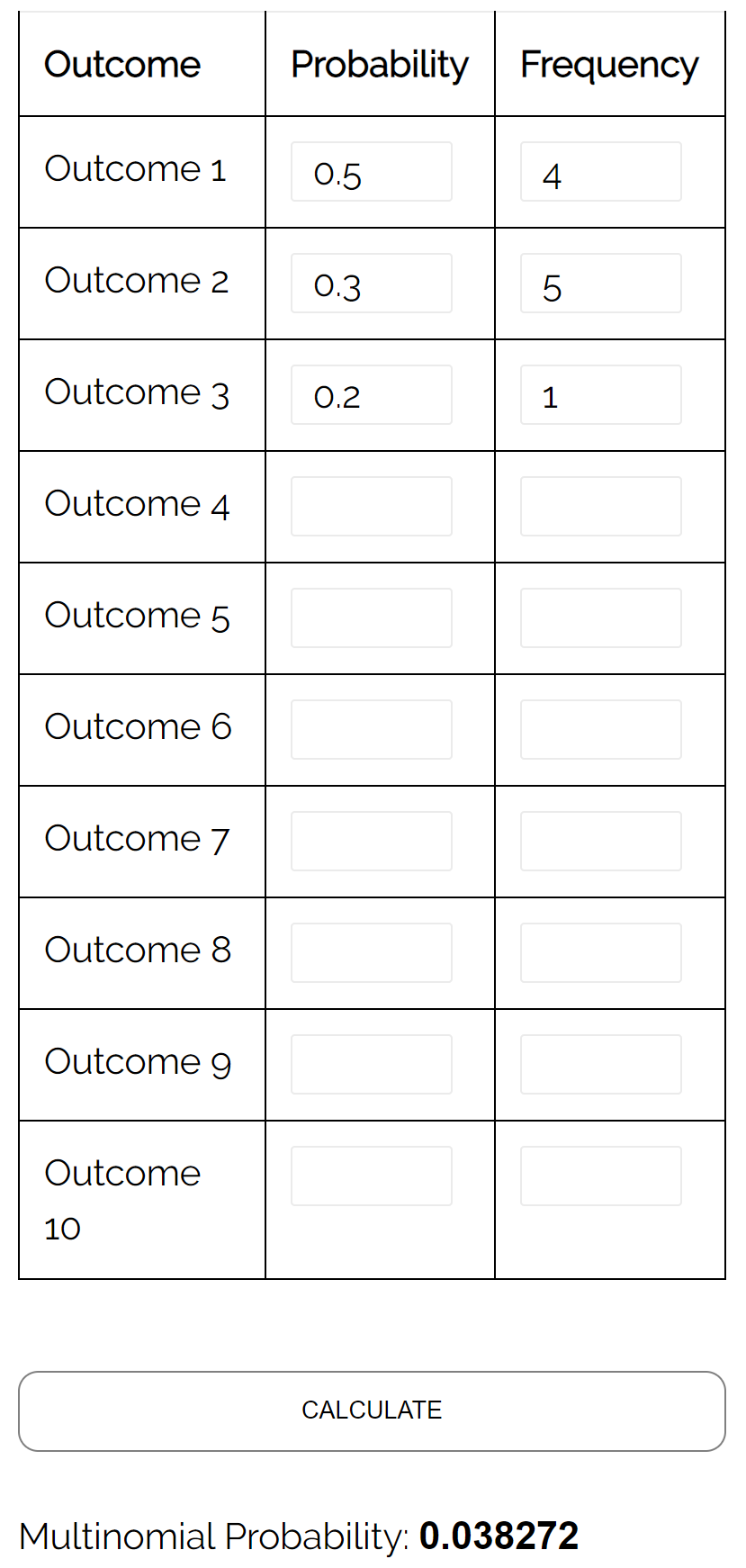
Frage: Angenommen, zwei Schüler spielen Schach gegeneinander. Die Wahrscheinlichkeit, dass Schüler A ein bestimmtes Spiel gewinnt, beträgt 0,5, die Wahrscheinlichkeit, dass Schüler B ein bestimmtes Spiel gewinnt, beträgt 0,3 und die Wahrscheinlichkeit, dass es in einem bestimmten Spiel ein Unentschieden gibt, beträgt 0,2. Wenn sie 10 Spiele spielen, wie hoch ist die Wahrscheinlichkeit, dass Schüler A ein bestimmtes Spiel gewinnt? Wahrscheinlichkeit, dass Spieler A 4 Mal gewinnt, Spieler B 5 Mal gewinnt und dass es 1 Mal Unentschieden gibt?

Antwort: Wenn wir den Multinomialverteilungsrechner mit den folgenden Eingaben verwenden, ermitteln wir, dass die Wahrscheinlichkeit 0,038272 beträgt:

Zusätzliche Ressourcen

Die folgenden Tutorials bieten eine Einführung in andere gängige Verteilungen in der Statistik:

Eine Einführung in die Normalverteilung
Eine Einführung in die Binomialverteilung
Eine Einführung in die Poisson-Verteilung
Eine Einführung in die geometrische Verteilung