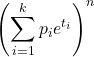Multinomiale verteilung

Von Dr. Benjamin Anderson August 4, 2023 Wahrscheinlichkeit Keine Kommentare

In diesem Artikel wird erklärt, was eine Multinomialverteilung in der Statistik ist. Sie finden also die Definition einer Multinomialverteilung, ihre Formel, eine gelöste Aufgabe und welche Eigenschaften diese Art von Wahrscheinlichkeitsverteilung hat. Darüber hinaus können Sie die Wahrscheinlichkeit einer Multinomialverteilung mit einem Online-Rechner berechnen.

Was ist eine Multinomialverteilung?

Die Multinomialverteilung (oder Multinomialverteilung ) ist eine Wahrscheinlichkeitsverteilung, die die Wahrscheinlichkeit beschreibt, dass mehrere sich gegenseitig ausschließende Ereignisse nach mehreren Versuchen mit einer bestimmten Häufigkeit auftreten.

Das heißt, wenn ein Zufallsexperiment zu drei oder mehr exklusiven Ereignissen führen kann und die Wahrscheinlichkeit, dass jedes Ereignis separat auftritt, bekannt ist, wird die Multinomialverteilung verwendet, um die Wahrscheinlichkeit zu berechnen, dass bei der Durchführung mehrerer Experimente eine bestimmte Anzahl von Ereignissen auftritt. Zeit jedes Mal.

Die Multinomialverteilung ist daher eine Verallgemeinerung der Binomialverteilung.

Multinomiale Verteilungsformel

Um eine multinomiale Verteilungswahrscheinlichkeit zu berechnen, müssen Sie zunächst den Quotienten zwischen der Fakultät der Gesamtzahl der Daten und den Fakultäten der Häufigkeit des Auftretens jedes Ereignisses bestimmen und das Ergebnis mit dem Produkt der Wahrscheinlichkeit jedes Ereignisses multiplizieren. auf die Häufigkeit des Auftretens dieses Ereignisses gebracht.

Mit anderen Worten lautet die Formel für die Multinomialverteilung wie folgt:

Gold:

$P$

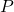
ist die Wahrscheinlichkeit der berechneten Multinomialverteilung.
$n$

ist die Gesamtzahl der durchgeführten Tests.
$x_i$

ist die Häufigkeit, mit der das Ereignis auftritt

$i$

.
$p_i$

ist die Wahrscheinlichkeit, dass das Ereignis eintritt

$i$

.

👉 Mit dem Rechner unten können Sie die Wahrscheinlichkeit einer Variablen berechnen, die der Multinomialverteilung folgt.

Beispiel für eine Multinomialverteilung

Um das Konzept der Multinomialverteilung vollständig zu verstehen, haben Sie unten ein Beispiel für die Berechnung der Wahrscheinlichkeit einer Multinomialverteilung gelöst.

Ein Geschäft verkauft drei verschiedene Produkte. Wenn ein Kunde einen Kauf tätigt, beträgt die Wahrscheinlichkeit, dass es sich um Produkt A, Produkt B oder Produkt C handelt, jeweils 30 %, 15 % und 55 %. Ermitteln Sie die Wahrscheinlichkeit, dass, wenn das Geschäft 8 Einheiten verkauft hat, 2 von Produkt A, 1 von Produkt B und 5 von Produkt C stammen.

Das definierte Problem unterliegt einer Multinomialverteilung, daher ist es notwendig, die Formel für diese Art von Wahrscheinlichkeitsverteilung anzuwenden:

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

Also setzen wir die Daten aus dem Problem in die Formel ein und führen die Wahrscheinlichkeitsberechnung durch:

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

Die Wahrscheinlichkeit, dass das, was in der Problemstellung steht, eintrifft, beträgt also 11,4 %.

Multinomialverteilungsrechner

Schreiben Sie die Häufigkeit des Auftretens jedes Ereignisses in das erste Feld und in der gleichen Reihenfolge die Eintrittswahrscheinlichkeit jedes Ereignisses in das zweite Feld. Geben Sie dann in das letzte leere Feld die Gesamtzahl der durchgeführten Versuche ein.

Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Eigenschaften der Multinomialverteilung

Die Multinomialverteilung weist folgende Merkmale auf:

In einer multinomialen Verteilung ist der erwartete Wert der Häufigkeit des Auftretens von Ereignis i bei der Durchführung von n Versuchen gleich der Gesamtzahl der durchgeführten Versuche multipliziert mit der Wahrscheinlichkeit des Eintretens des Ereignisses.

$E[x_i]=n\cdot p_i$

In einer multinomialen Verteilung wird die Varianz für Ereignis i mithilfe des folgenden Ausdrucks berechnet:

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

In ähnlicher Weise entspricht die Kovarianz zwischen zwei Ereignissen dem Produkt aus der Gesamtzahl der Versuche multipliziert mit der Wahrscheinlichkeit jedes Ereignisses multipliziert mit -1:

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

Die momenterzeugende Funktion für eine Multinomialverteilung ist:

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen