Multiple lineare regression von hand (schritt für schritt)
Die multiple lineare Regression ist eine Methode, mit der wir die Beziehung zwischen zwei oder mehr Prädiktorvariablen und einer Antwortvariablen quantifizieren können.
In diesem Tutorial wird erläutert, wie Sie manuell eine multiple lineare Regression durchführen.
Beispiel: Multiple lineare Regression von Hand
Angenommen, wir haben den folgenden Datensatz mit einer Antwortvariablen y und zwei Prädiktorvariablen x 1 und x 2 :
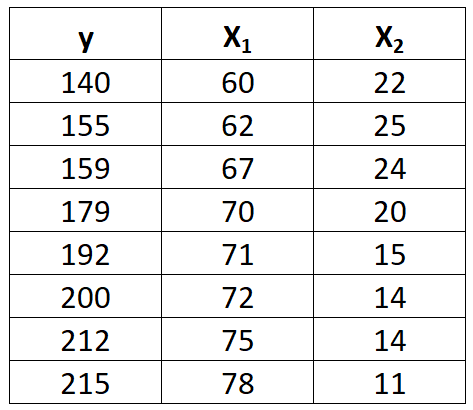
Führen Sie die folgenden Schritte aus, um ein multiples lineares Regressionsmodell an diesen Datensatz anzupassen.
Schritt 1: Berechnen Sie x 1 2 , x 2 2 , x 1 y, x 2 y und x 1 x 2 .
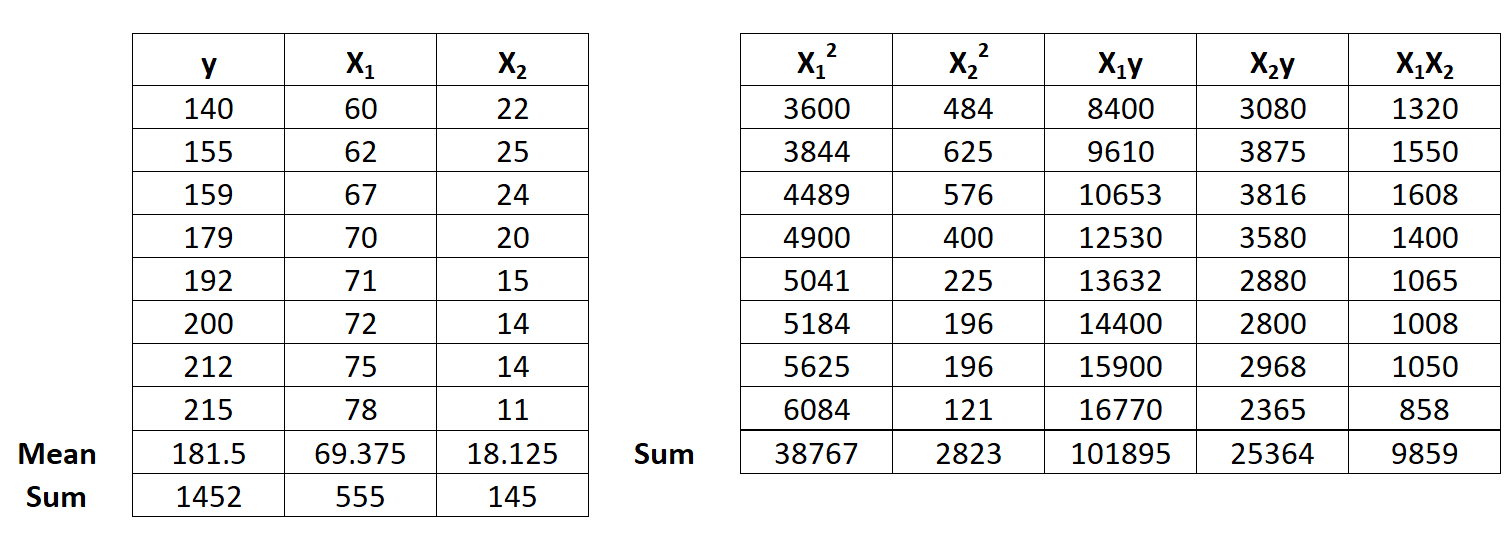
Schritt 2: Berechnen Sie die Regressionssummen.
Führen Sie als Nächstes die folgenden Regressionssummenberechnungen durch:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38,767 – (555) 2 / 8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194,875
- Σ x 1 y = Σ
- Σ x 2 y = Σ
- Σ x 1 x 2 = Σ
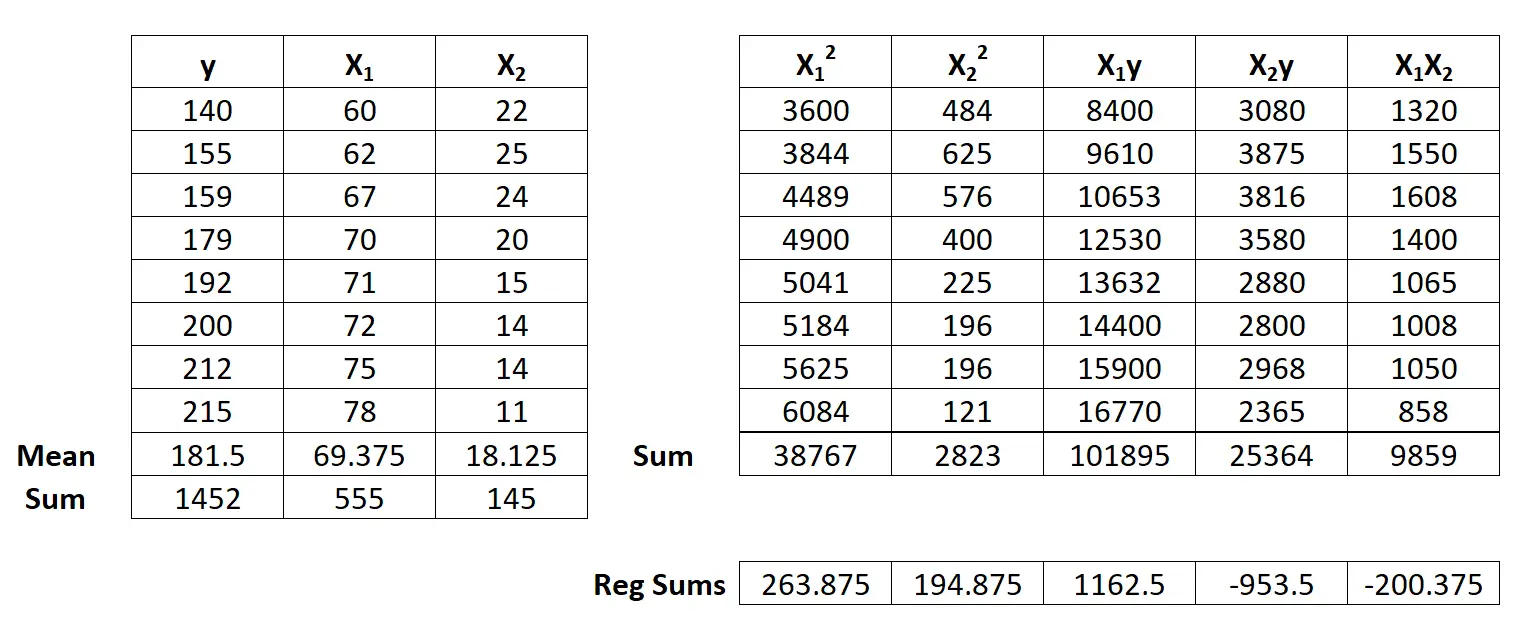
Schritt 3: Berechnen Sie b 0 , b 1 und b 2 .
Die Formel zur Berechnung von b 1 lautet: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Also ist b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
Die Formel zur Berechnung von b 2 lautet: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Also, b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
Die Formel zur Berechnung von b 0 lautet: y – b 1 X 1 – b 2 X 2
Somit ist b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Schritt 5: Platzieren Sie b 0 , b 1 und b 2 in der geschätzten linearen Regressionsgleichung.
Die geschätzte lineare Regressionsgleichung lautet: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
In unserem Beispiel ist es ŷ = -6,867 + 3,148x 1 – 1,656x 2
So interpretieren Sie eine multiple lineare Regressionsgleichung
So interpretieren Sie diese geschätzte lineare Regressionsgleichung: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6,867 . Wenn beide Prädiktorvariablen gleich Null sind, beträgt der Durchschnittswert von y -6,867.
b1 = 3,148 . Ein Anstieg von x 1 um eine Einheit ist im Durchschnitt mit einem Anstieg von y um 3,148 Einheiten verbunden, vorausgesetzt, x 2 bleibt konstant.
b2 = -1,656 . Ein Anstieg von x 2 um eine Einheit ist im Durchschnitt mit einem Rückgang von y um 1.656 Einheiten verbunden, vorausgesetzt, x 1 bleibt konstant.
Zusätzliche Ressourcen
Eine Einführung in die multiple lineare Regression
So führen Sie eine einfache lineare Regression manuell durch
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen