Negative korrelation

Dieser Artikel erklärt, was die negative Korrelation zwischen zwei statistischen Variablen ist, und zeigt ein Beispiel für diese Art von Korrelation. Darüber hinaus können Sie sehen, wie die negative Korrelation interpretiert wird.

Was ist eine negative Korrelation?

In der Statistik ist eine negative Korrelation eine Art Korrelation zwischen zwei verschiedenen Variablen, die darauf hinweist, dass sie in umgekehrter Beziehung zueinander stehen. Das heißt, wenn zwei Variablen eine negative Korrelation aufweisen, bedeutet dies, dass der Wert einer Variablen zunimmt und der Wert der anderen Variable abnimmt.

Wenn zwei Variablen eine negative Korrelation aufweisen, liegt der Wert des Korrelationskoeffizienten zwischen -1 (einschließlich) und 0 (nicht einschließlich).

Negative Korrelation wird in der Statistik auch als inverse Korrelation bezeichnet.

Beispiel für negative Korrelation

Nachdem wir nun die Definition der negativen Korrelation kennen, sehen wir uns zum besseren Verständnis des Konzepts ein Beispiel für zwei Variablen mit dieser Art von Korrelation an.

• Ein internationales Unternehmen zeichnete in einer Datentabelle die Durchschnittstemperatur für den Monat und die Verkäufe von Pullovern auf, die in diesem Monat in mehreren seiner Filialen hergestellt wurden. Analysieren Sie die Korrelation zwischen diesen beiden statistischen Variablen.

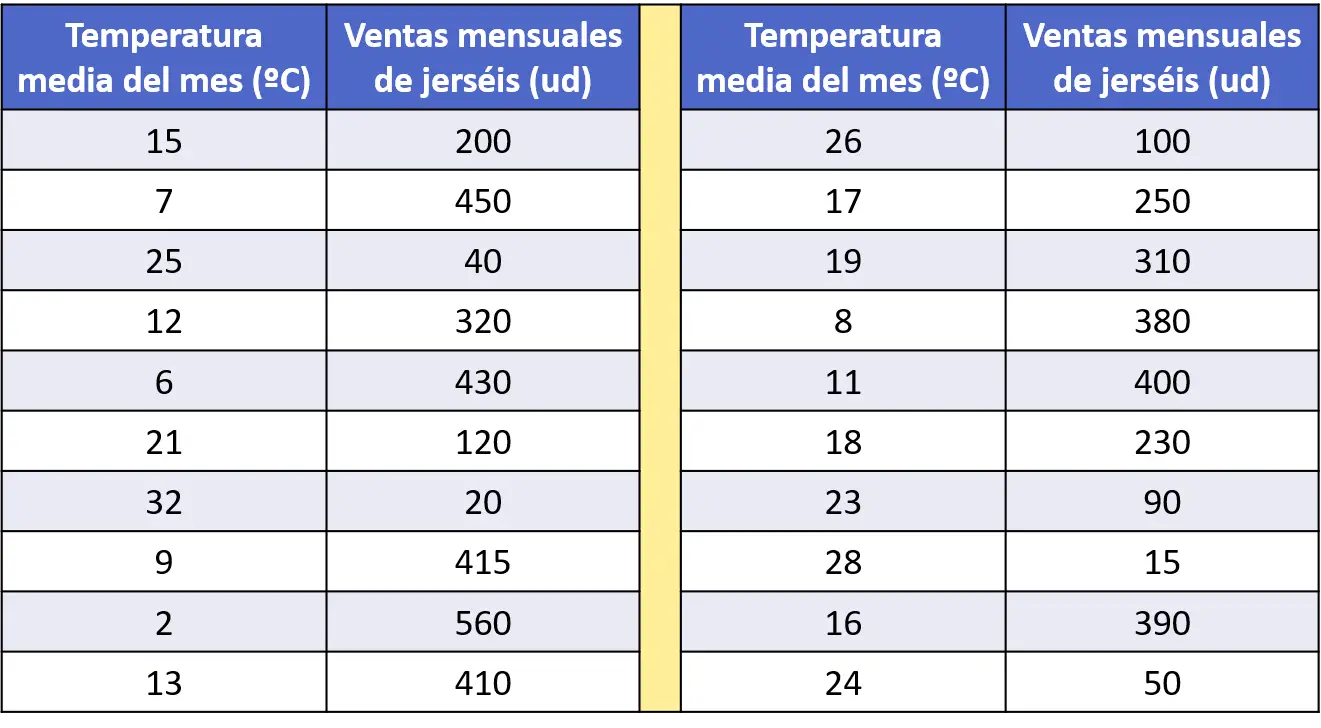
Um die Korrelation zwischen diesen beiden Variablen zu untersuchen, müssen wir zunächst den Datensatz in einem Diagramm darstellen. Daher erstellen wir das Streudiagramm der Datenpaare:

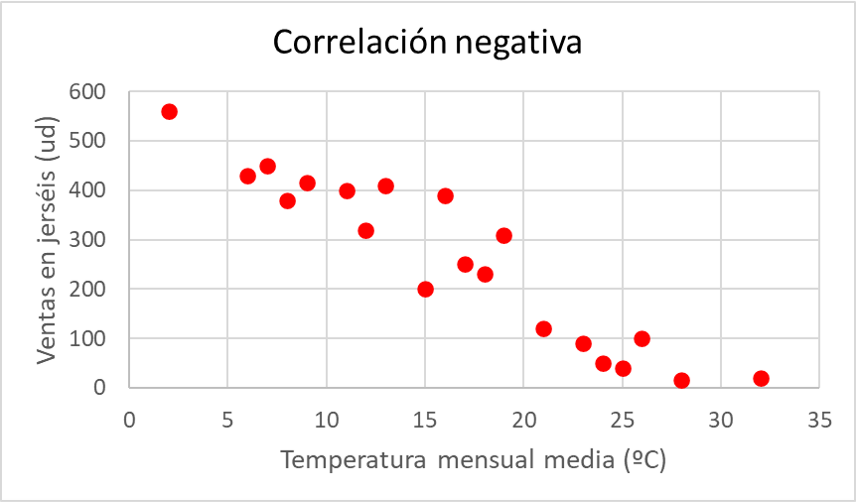
Wie Sie dem Streudiagramm entnehmen können, scheint die Korrelation zwischen den beiden Variablen zunächst negativ zu sein, denn wenn die eine zunimmt, nimmt die andere ab und umgekehrt. Es ist jedoch notwendig, die Korrelation zwischen den Variablen durch Berechnung des Korrelationskoeffizienten zu überprüfen:

Der Wert des Korrelationskoeffizienten ist negativ, daher wird bestätigt, dass die Korrelation zwischen den beiden untersuchten Variablen negativ ist.

Interpretation der negativen Korrelation

In diesem Abschnitt erfahren Sie, wie Sie den Wert einer negativen Korrelation zwischen zwei Variablen interpretieren, damit Sie die Bedeutung einer negativen Korrelation besser verstehen.

Je kleiner der negative Korrelationskoeffizient ist, desto negativer korrelieren die beiden Variablen. Wenn also der Korrelationskoeffizient zwischen zwei Variablen sehr nahe bei -1 liegt, ist die negative Korrelation umso signifikanter. Liegt der Wert des Korrelationskoeffizienten hingegen nahe bei 0, bedeutet dies, dass die Korrelation zwischen den beiden Variablen schwach ist.

Wenn der Korrelationskoeffizient außerdem 0 wird, ist die Korrelation zwischen den Variablen Null. Und selbst wenn der Koeffizientenwert positiv ist, bedeutet dies, dass die Korrelation positiv ist. Im Folgenden werden wir die verschiedenen Arten der Korrelation diskutieren.

Schließlich sollten Sie bedenken, dass eine negative Korrelation keine Kausalität zwischen den Variablen bedeutet. Das heißt, wenn zwei Variablen eine negative Korrelation aufweisen, bedeutet dies, dass sie linear und negativ miteinander verbunden sind, die Ursache für den Anstieg einer Variablen jedoch nicht unbedingt der Rückgang der anderen Variablen ist.

Weitere Informationen finden Sie im folgenden Artikel:

Negative, positive und Nullkorrelation

In diesem Artikel haben wir uns darauf konzentriert, was eine negative Korrelation ist. In der Statistik können jedoch zwei Variablen auch eine positive Korrelation oder eine Nullkorrelation aufweisen.

• Positive Korrelation – Eine Variable nimmt zu, wenn auch die andere zunimmt. Der Wert des Korrelationskoeffizienten liegt zwischen 0 (nicht enthalten) und 1 (einschließlich).
• Negative Korrelation : Wenn eine Variable zunimmt, nimmt die andere ab, und umgekehrt, wenn eine Variable abnimmt, nimmt die andere zu. Der Wert des Korrelationskoeffizienten liegt zwischen -1 (einschließlich) und 0 (nicht einschließlich).
• Nullkorrelation : Es besteht keine Beziehung zwischen den beiden Variablen. Der Korrelationskoeffizient ist gleich 0.

In den folgenden Diagrammen können Sie die verschiedenen dargestellten Korrelationstypen sehen: