Negatives binomial vs. poisson: so wählen sie ein regressionsmodell aus

Negative binomiale Regression und Poisson-Regression sind zwei Arten von Regressionsmodellen, die verwendet werden sollten, wenn die Antwortvariable durch diskrete Zählergebnisse dargestellt wird.

Hier sind einige Beispiele für Antwortvariablen, die diskrete Zählergebnisse darstellen:

• Die Anzahl der Studierenden, die einen bestimmten Studiengang abschließen
• Die Anzahl der Verkehrsunfälle an einer bestimmten Kreuzung
• Die Anzahl der Teilnehmer, die einen Marathon absolvieren
• Die Anzahl der Retouren in einem bestimmten Monat in einem Einzelhandelsgeschäft

Wenn die Varianz ungefähr dem Mittelwert entspricht, passt ein Poisson-Regressionsmodell im Allgemeinen gut zu einem Datensatz.

Wenn die Varianz jedoch deutlich größer als der Mittelwert ist, ist ein negatives binomiales Regressionsmodell im Allgemeinen in der Lage, die Daten besser anzupassen.

Es gibt zwei Techniken, mit denen wir bestimmen können, ob die Poisson-Regression oder die negative binomiale Regression für einen bestimmten Datensatz besser geeignet ist:

1. Restparzellen

Wir können ein Diagramm der standardisierten Residuen gegenüber den vorhergesagten Werten aus einem Regressionsmodell erstellen.

Wenn die Mehrheit der standardisierten Residuen zwischen -2 und 2 liegt, ist wahrscheinlich ein Poisson-Regressionsmodell geeignet.

Wenn jedoch viele Residuen außerhalb dieses Bereichs liegen, liefert ein negatives binomiales Regressionsmodell wahrscheinlich eine bessere Anpassung.

2. Likelihood-Ratio-Test

Wir können ein Poisson-Regressionsmodell und ein negatives Binomial-Regressionsmodell an denselben Datensatz anpassen und dann einen Likelihood-Ratio-Test durchführen.

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (z. B. 0,05), können wir daraus schließen, dass das negative binomiale Regressionsmodell eine deutlich bessere Anpassung liefert.

Das folgende Beispiel zeigt, wie diese beiden Techniken in R verwendet werden, um zu bestimmen, ob es besser ist, für einen bestimmten Datensatz eine Poisson-Regression oder ein negatives Binomial-Regressionsmodell zu verwenden.

Beispiel: negative binomiale Regression vs. Poisson-Regression

Angenommen, wir möchten wissen, wie viele Stipendien ein High-School-Baseballspieler in einem bestimmten Landkreis basierend auf seiner Schulklasse („A“, „B“ oder „C“) und seiner Schulnote erhält. Hochschulaufnahmeprüfung (gemessen von 0 bis 100). ).

Verwenden Sie die folgenden Schritte, um zu bestimmen, ob ein negatives binomiales Regressionsmodell oder ein Poisson-Regressionsmodell eine bessere Anpassung an die Daten bietet.

Schritt 1: Erstellen Sie die Daten

Der folgende Code erstellt den Datensatz, mit dem wir arbeiten werden, der Daten zu 1.000 Baseballspielern enthält:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

Schritt 2: Passen Sie ein Poisson-Regressionsmodell und ein negatives Binomial-Regressionsmodell an

Der folgende Code zeigt, wie sowohl ein Poisson-Regressionsmodell als auch ein negatives Binomial-Regressionsmodell an die Daten angepasst werden:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

Schritt 3: Erstellen Sie Restdiagramme

Der folgende Code zeigt, wie Residuendiagramme für beide Modelle erstellt werden.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

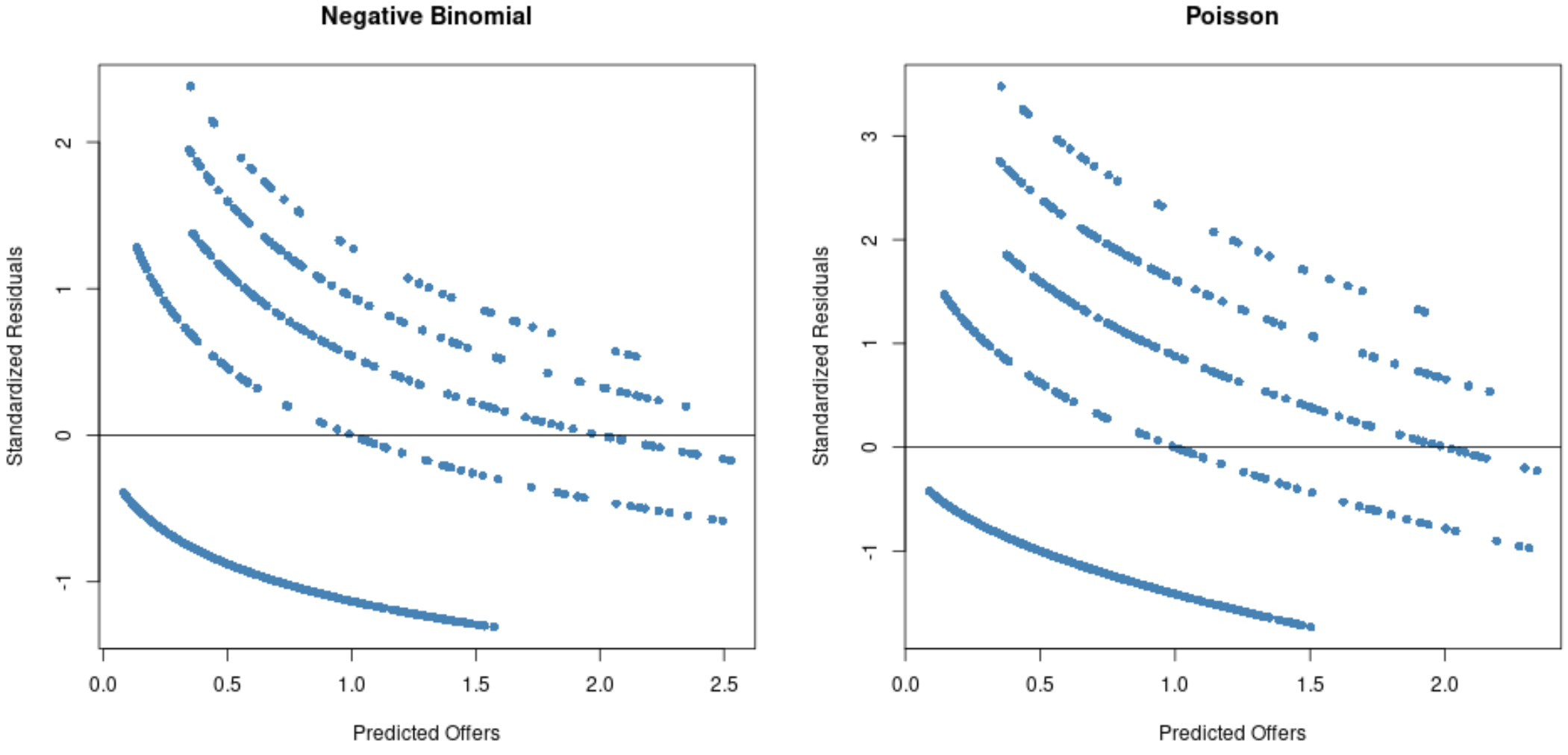
Aus den Diagrammen können wir ersehen, dass die Residuen beim Poisson-Regressionsmodell stärker verteilt sind (beachten Sie, dass einige Residuen über 3 hinausgehen) im Vergleich zum negativen binomialen Regressionsmodell.

Dies ist ein Zeichen dafür, dass ein negatives binomiales Regressionsmodell wahrscheinlich besser geeignet ist, da die Residuen dieses Modells kleiner sind.

Schritt 4: Führen Sie einen Likelihood-Ratio-Test durch

Schließlich können wir einen Likelihood-Ratio-Test durchführen, um festzustellen, ob es einen statistisch signifikanten Unterschied in der Anpassung der beiden Regressionsmodelle gibt:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

Der p-Wert des Tests beträgt 3,508072e-29 , was deutlich weniger als 0,05 ist.

Wir kommen daher zu dem Schluss, dass das negative binomiale Regressionsmodell im Vergleich zum Poisson-Regressionsmodell eine deutlich bessere Anpassung an die Daten liefert.

Zusätzliche Ressourcen

Eine Einführung in die negative Binomialverteilung
Eine Einführung in die Poisson-Verteilung