So berechnen sie normalcdf-wahrscheinlichkeiten in excel

Die NormalCDF- Funktion auf einem TI-83- oder TI-84-Rechner kann verwendet werden, um die Wahrscheinlichkeit zu ermitteln, dass eine normalverteilte Zufallsvariable einen Wert innerhalb eines bestimmten Bereichs annimmt.

Auf einem TI-83- oder TI-84-Rechner verwendet diese Funktion die folgende Syntax

normalcdf (unten, oben, μ, σ)

Gold:

• niedriger = unterer Wert des Bereichs
• Upper = oberer Wert des Bereichs
• μ = Bevölkerungsmittelwert
• σ = Populationsstandardabweichung

Angenommen, eine Zufallsvariable ist normalverteilt mit einem Mittelwert von 50 und einer Standardabweichung von 4. Die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert zwischen 48 und 52 annimmt, kann wie folgt berechnet werden:

normalcdf(48, 52, 50, 4) = 0,3829

Wir können diese Antwort in Excel mit der Funktion NORM.DIST() reproduzieren, die die folgende Syntax verwendet:

NORM.DIST(x, σ, μ, kumulativ)

Gold:

• x = individueller Datenwert
• μ = Bevölkerungsmittelwert
• σ = Populationsstandardabweichung
• kumulativ = FALSE PDF berechnen; TRUE berechnet den CDF

Die folgenden Beispiele zeigen, wie Sie diese Funktion in der Praxis nutzen können.

Beispiel 1: Wahrscheinlichkeit zwischen zwei Werten

Angenommen, eine Zufallsvariable ist normalverteilt mit einem Mittelwert von 50 und einer Standardabweichung von 4. Die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert zwischen 48 und 52 annimmt, kann wie folgt berechnet werden:

 =NORM. DIST (52, 50, 4, TRUE ) - NORM. DIST (48, 50, 4, TRUE )

Das folgende Bild zeigt, wie diese Berechnung in Excel durchgeführt wird:

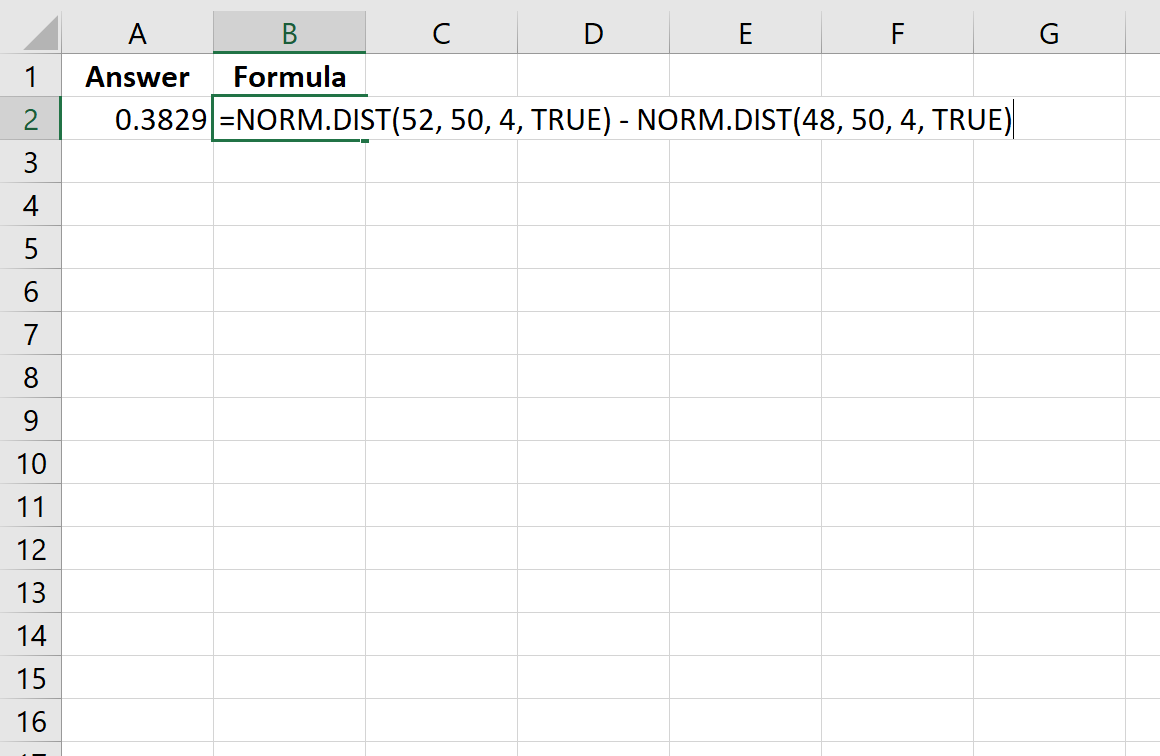
Die Wahrscheinlichkeit beträgt 0,3829.

Beispiel 2: Wahrscheinlichkeit kleiner als ein Wert

Angenommen, eine Zufallsvariable ist normalverteilt mit einem Mittelwert von 50 und einer Standardabweichung von 4. Die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert kleiner als 48 annimmt, kann wie folgt berechnet werden:

 =NORM. DIST (48, 50, 4, TRUE )

Das folgende Bild zeigt, wie diese Berechnung in Excel durchgeführt wird:

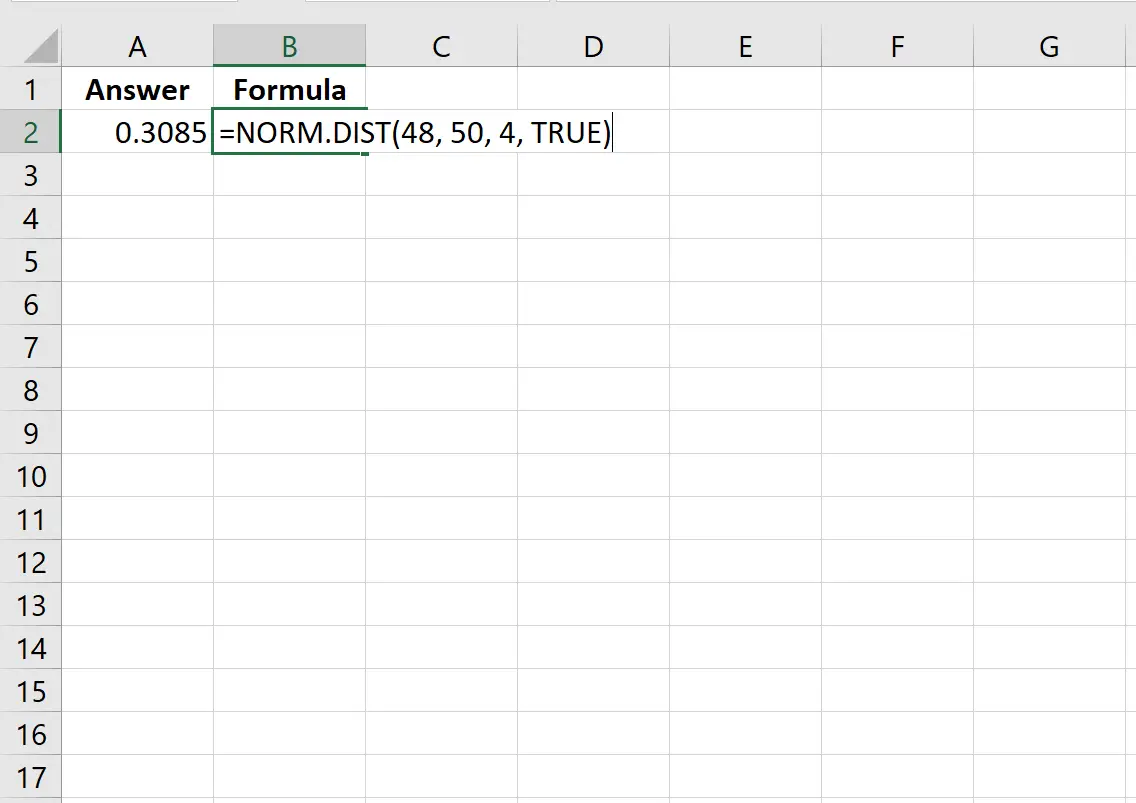
Die Wahrscheinlichkeit beträgt 0,3085.

Beispiel 3: Wahrscheinlichkeit größer als ein Wert

Angenommen, eine Zufallsvariable ist normalverteilt mit einem Mittelwert von 50 und einer Standardabweichung von 4. Die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert größer als 55 annimmt, kann wie folgt berechnet werden:

 =1 - NORM. DIST (55, 50, 4, TRUE )

Das folgende Bild zeigt, wie diese Berechnung in Excel durchgeführt wird:

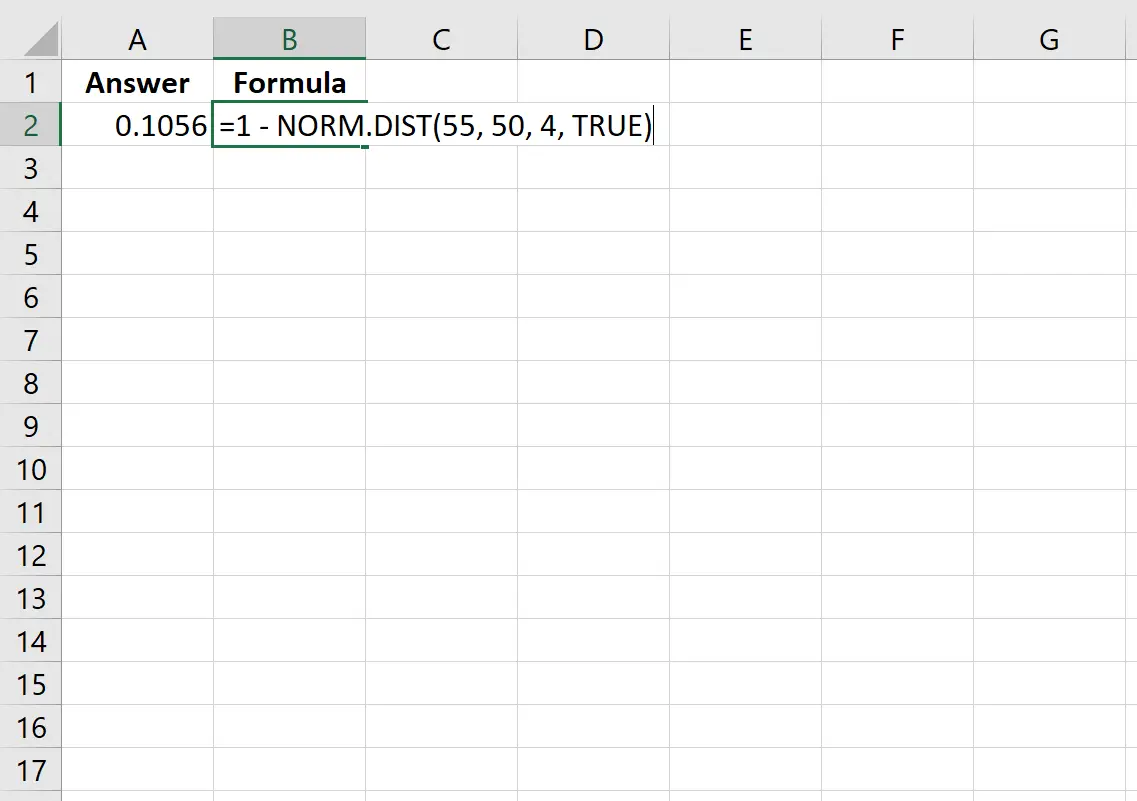
Die Wahrscheinlichkeit beträgt 0,1056.

Zusätzliche Ressourcen

Sie können diesen normalen CDF-Rechner auch verwenden, um automatisch die mit einer Normalverteilung verbundenen Wahrscheinlichkeiten zu ermitteln.