Standardnormalverteilung
In diesem Artikel wird erklärt, was die Standardnormalverteilung ist und wofür sie verwendet wird. Außerdem finden Sie hier die Eigenschaften der Standardnormalverteilung, die Tabelle mit ihren Kennwerten und zusätzlich eine gelöste Aufgabe.
Was ist die Standardnormalverteilung?
Die Standardnormalverteilung , auch Einheitsnormalverteilung genannt, ist der einfachste Fall einer Normalverteilung. Genauer gesagt ist die Standardnormalverteilung eine Normalverteilung mit Mittelwert und Standardabweichungswert gleich 0 bzw. 1.
Daher ist die Standardnormalverteilung als N(0,1) definiert, wobei der erste Parameter der Mittelwert der Verteilung und der zweite Parameter ihre Standardabweichung (oder SD) ist.
![Rendered by QuickLaTeX.com \displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ca26cb58ac445099df12aeebda27e38_l3.png)
Der Graph der Standardnormalverteilung sieht daher wie folgt aus:
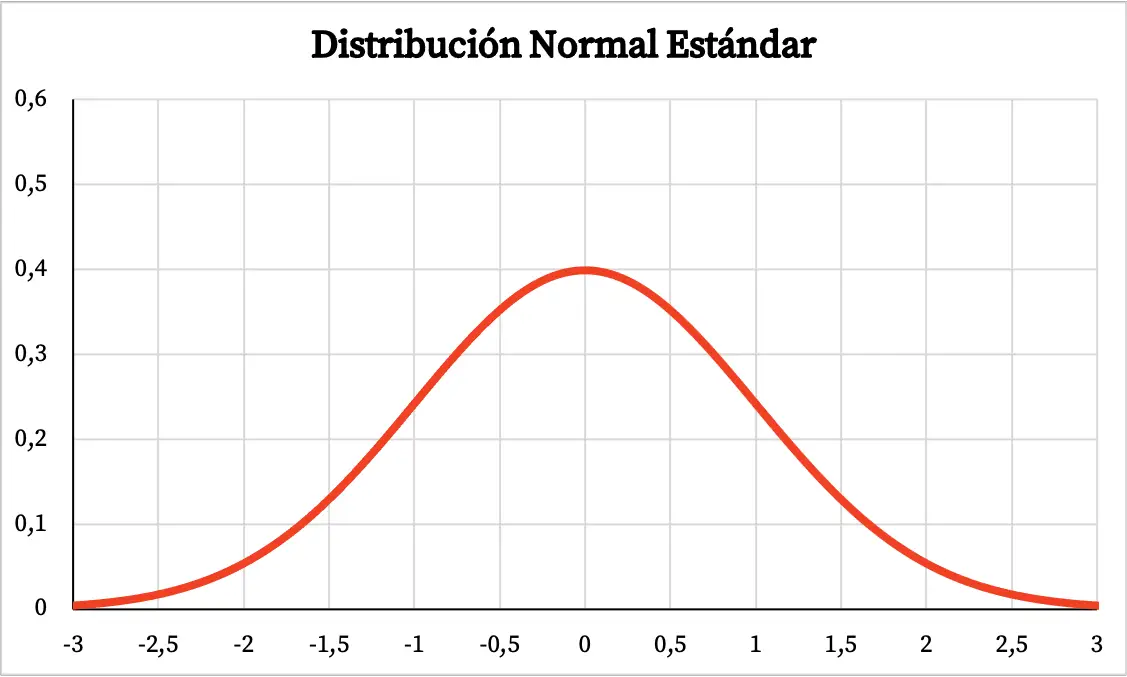
Formel für die Standardnormalverteilung
Um eine beliebige Normalverteilung in eine Standardnormalverteilung umzuwandeln, müssen Sie den Mittelwert der Normalverteilung von allen ihren Werten subtrahieren und dann durch die Standardabweichung der Normalverteilung dividieren.
Die Formel für die Standardnormalverteilung lautet daher wie folgt:
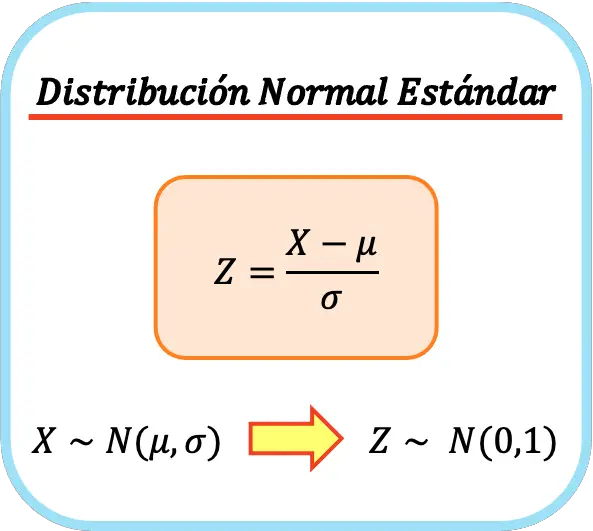
Auf diese Weise betragen das arithmetische Mittel und die Standardabweichung der neuen Variablen 0 bzw. 1, sodass wir eine Standardnormalverteilung erhalten. Dieser Vorgang wird auch als univariate Normalisierung oder univariate Normalisierung bezeichnet.
Standard-Normalverteilungstabelle
Die Tabelle einer Standardnormalverteilung ist eine Tabelle, die die Wahrscheinlichkeiten enthält, dass ein beobachteter Wert kleiner als ein gegebener Wert der Standardnormalverteilung ist.
Da die Funktion einer Normalverteilung außerdem von ihrem Mittelwert und ihrer Standardabweichung abhängt, wird die Standardnormalverteilungstabelle im weiteren Sinne auch zur Bestimmung der Wahrscheinlichkeiten jeder Normalverteilung verwendet. Dazu wird die Normalverteilung in eine Standardnormalverteilung eingetippt und wir schauen dann in der Tabelle nach, welche Wahrscheinlichkeit ihr entspricht.
Die Werte in der Standardnormalverteilungstabelle lauten also wie folgt:

Beispiel einer Standardnormalverteilung
Nachdem wir nun die Definition der Standardnormalverteilung und ihre Formel kennen, finden Sie unten ein konkretes Beispiel, um das Konzept gut zu verstehen.
- Eine kontinuierliche Zufallsvariable folgt einer Normalverteilung mit einem Mittelwert von 45 und einer Standardabweichung von 15. Wie groß ist die Wahrscheinlichkeit, einen Wert kleiner oder gleich 58 zu erhalten?
![]()
Um die Wahrscheinlichkeit einer Normalverteilung zu ermitteln, müssen wir ihre Merkmalstabelle verwenden. Dazu müssen wir jedoch zunächst den Eingabevorgang durchführen, um die Standardnormalverteilung zu erhalten. Wir verwenden daher die Standardnormalverteilungsformel:
![]()
Wir subtrahieren also den Mittelwert vom Wahrscheinlichkeitswert und dividieren ihn dann durch die Standardabweichung
![]()
Sobald wir die Variable standardisiert haben, gehen wir zur Standardnormalverteilungswahrscheinlichkeitstabelle (siehe oben), um zu sehen, welcher Wahrscheinlichkeit der Wert von 0,87 entspricht:
![]()
Die Wahrscheinlichkeit, einen Wert kleiner oder gleich 58 zu erhalten, liegt somit bei 80,78 %.
Merkmale der Standardnormalverteilung
Die Standardnormalverteilung weist die folgenden Merkmale auf:
- Die Standardnormalverteilung ist eine symmetrische Verteilung mit dem Mittelpunkt 0.
- Wie eine Normalverteilung ist das Standardnormalverteilungsdiagramm glockenförmig, wobei der größte Teil der Diagrammfläche um den Mittelwert herum liegt.
- Daher haben Mittelwert, Modus und Median einer Normalverteilung den gleichen Wert, der 0 ist.
- Die Standardnormalverteilung hat ein Maximum bei z=0.
- Ebenso hat die Standardnormalverteilung zwei Wendepunkte, bei z=-1 und z=+1.
- Nach der Faustregel wissen wir, dass 68 % der Werte in einer Standardnormalverteilung zwischen +1 und -1 liegen, 95 % der Werte zwischen +2 und -2 und 99,7 % der Werte zwischen + 3 und – 3.