So berechnen und zeichnen sie normale cdf in python

Eine kumulative Verteilungsfunktion ( CDF ) gibt uns die Wahrscheinlichkeit an, mit der eine Zufallsvariable einen Wert annimmt, der kleiner oder gleich einem bestimmten Wert ist.

In diesem Tutorial wird erklärt, wie man normale CDF-Werte in Python berechnet und darstellt.

Beispiel 1: Berechnen Sie normale CDF-Wahrscheinlichkeiten in Python

Der einfachste Weg, normale CDF-Wahrscheinlichkeiten in Python zu berechnen, ist die Verwendung der Funktion norm.cdf() aus der SciPy- Bibliothek.

Der folgende Code zeigt, wie die Wahrscheinlichkeit berechnet wird, dass eine Zufallsvariable in einer Standardnormalverteilung einen Wert kleiner als 1,96 annimmt:

 from scipy. stats import norm

#calculate probability that random value is less than 1.96 in normal CDF
norm. cdf ( 1.96 )

0.9750021048517795

Die Wahrscheinlichkeit, dass eine Zufallsvariable in einer Standardnormalverteilung einen Wert kleiner als 1,96 annimmt, beträgt ungefähr 0,975 .

Wir können die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert größer als 1,96 annimmt, auch ermitteln, indem wir diesen Wert einfach von 1 subtrahieren:

 from scipy. stats import norm

#calculate probability that random value is greater than 1.96 in normal CDF
1 - norm. cdf ( 1.96 )

0.024997895148220484

Die Wahrscheinlichkeit, dass eine Zufallsvariable in einer Standardnormalverteilung einen Wert größer als 1,96 annimmt, beträgt etwa 0,025 .

Beispiel 2: Zeichnen des normalen CDF

Der folgende Code zeigt, wie man ein normales CDF in Python plottet:

 import matplotlib. pyplot as plt
import numpy as np
import scipy. stats as ss

#define x and y values to use for CDF
x = np. linspace (-4, 4, 1000)
y = ss. norm . cdf (x)

#normal plot CDF
plt. plot (x, y) 

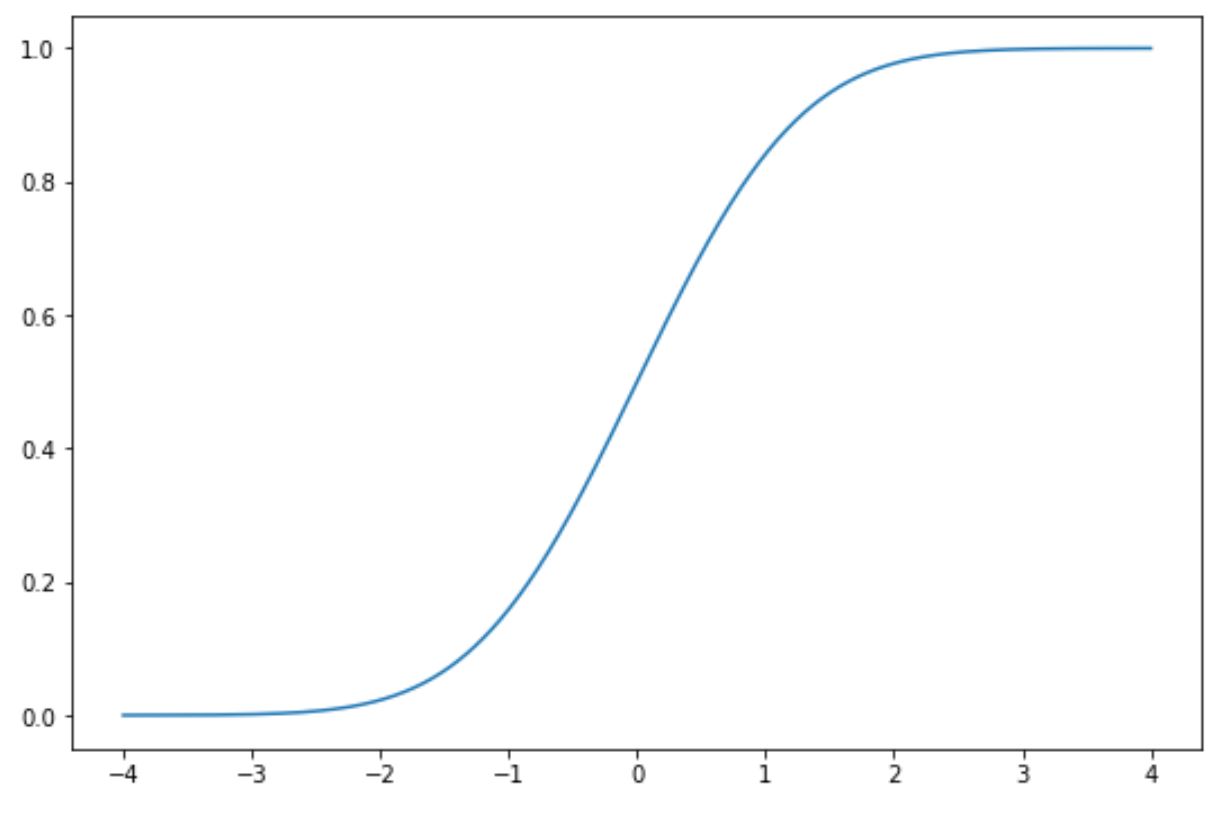
Die x-Achse zeigt die Werte einer Zufallsvariablen, die einer Standardnormalverteilung folgt, und die y-Achse zeigt die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert annimmt, der kleiner ist als der auf der x-Achse angezeigte Wert.

Wenn wir beispielsweise x = 1,96 betrachten, werden wir sehen, dass die kumulative Wahrscheinlichkeit, dass x kleiner als 1,96 ist, ungefähr 0,975 beträgt.

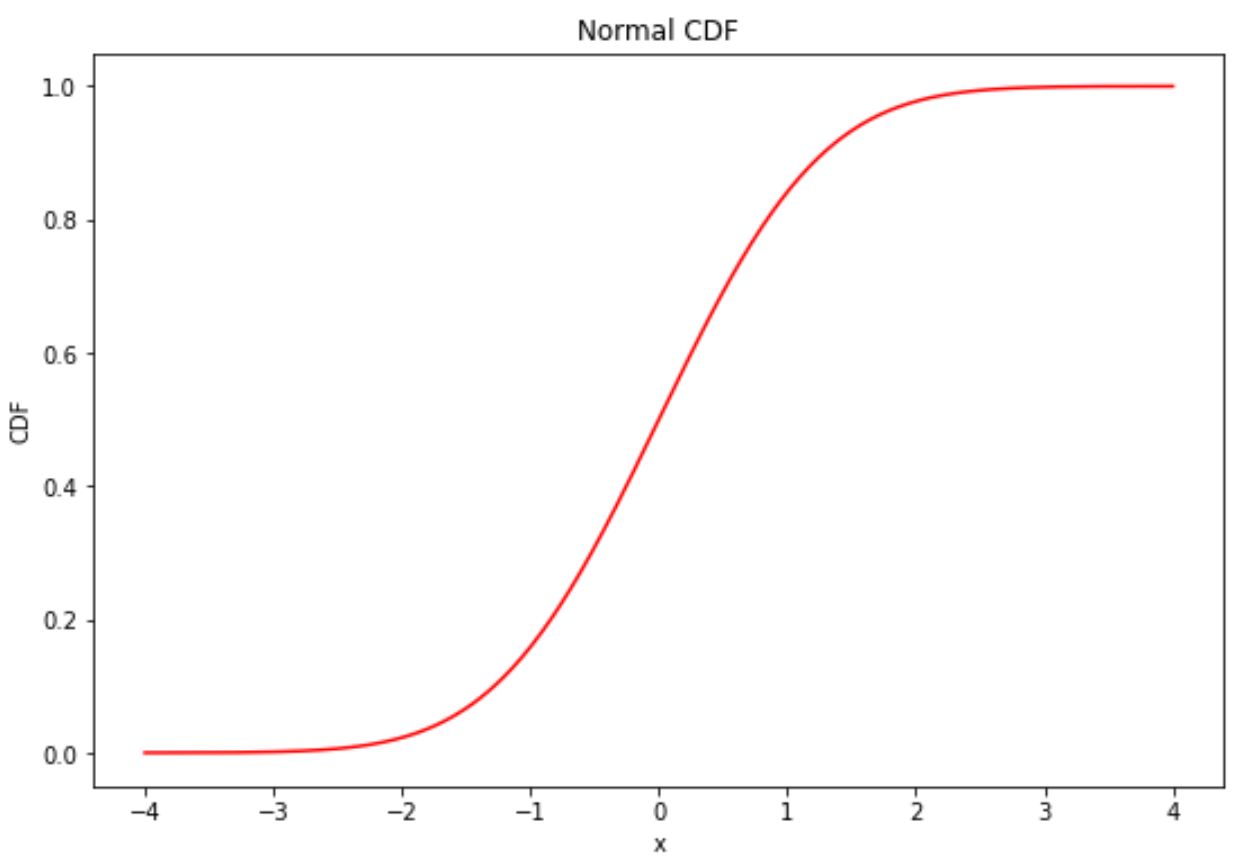
Fühlen Sie sich frei, auch die Farben und Beschriftungen der Achsen des normalen CDF-Diagramms zu ändern:

 import matplotlib. pyplot as plt
import numpy as np
import scipy. stats as ss

#define x and y values to use for CDF
x = np. linspace (-4, 4, 1000)
y = ss. norm . cdf (x)

#normal plot CDF
plt. plot (x,y,color=' red ')
plt. title (' Normal CDF ')
plt. xlabel (' x ')
plt. ylabel (' CDF ')

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige Vorgänge in Python ausführen:

So generieren Sie eine Normalverteilung in Python
So zeichnen Sie eine Normalverteilung in Python