So testen sie die normalität in r (4 methoden)

Viele statistische Tests gehen davon aus , dass Datensätze normalverteilt sind.

Es gibt vier gängige Methoden, diese Annahme in R zu überprüfen:

1. (Visuelle Methode) Erstellen Sie ein Histogramm.

• Wenn das Histogramm annähernd „glockenförmig“ ist, wird davon ausgegangen, dass die Daten normalverteilt sind.

2. (Visuelle Methode) Erstellen Sie ein QQ-Diagramm.

• Wenn die Punkte im Diagramm ungefähr auf einer geraden diagonalen Linie liegen, wird davon ausgegangen, dass die Daten normalverteilt sind.

3. (Formeller statistischer Test) Führen Sie einen Shapiro-Wilk-Test durch.

• Wenn der p-Wert des Tests größer als α = 0,05 ist, wird davon ausgegangen, dass die Daten normalverteilt sind.

4. (Formeller statistischer Test) Führen Sie einen Kolmogorov-Smirnov-Test durch.

• Wenn der p-Wert des Tests größer als α = 0,05 ist, wird davon ausgegangen, dass die Daten normalverteilt sind.

Die folgenden Beispiele zeigen, wie jede dieser Methoden in der Praxis angewendet werden kann.

Methode 1: Erstellen Sie ein Histogramm

Der folgende Code zeigt, wie man in R ein Histogramm für einen normalverteilten und nicht normalverteilten Datensatz erstellt:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

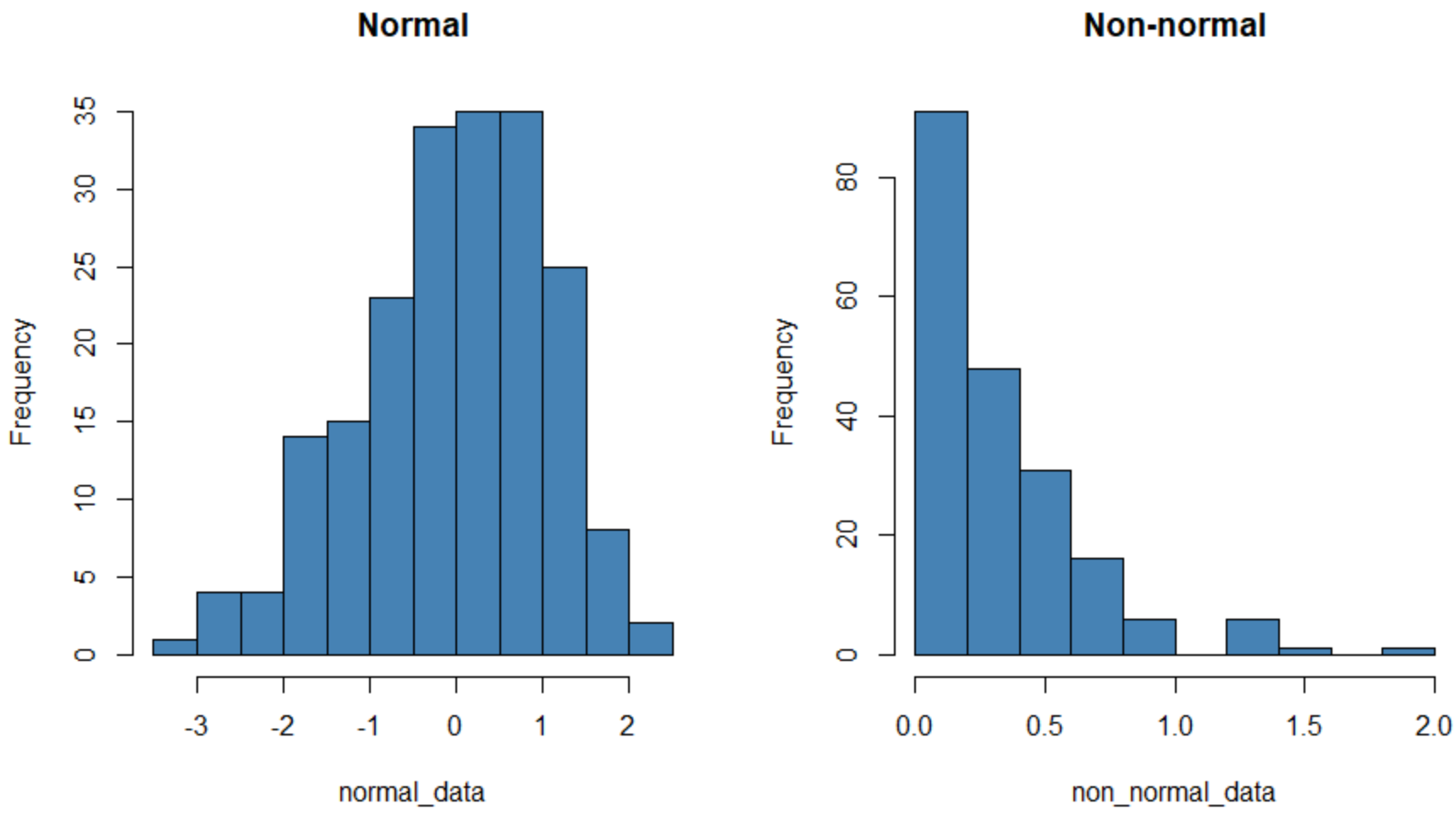
Das Histogramm auf der linken Seite zeigt einen Datensatz, der normalverteilt (ungefähr „glockenförmig“) ist, und das Histogramm auf der rechten Seite zeigt einen Datensatz, der nicht normalverteilt ist.

Methode 2: Erstellen Sie ein QQ-Diagramm

Der folgende Code zeigt, wie man ein QQ-Diagramm für einen normalverteilten und nicht normalverteilten Datensatz in R erstellt:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

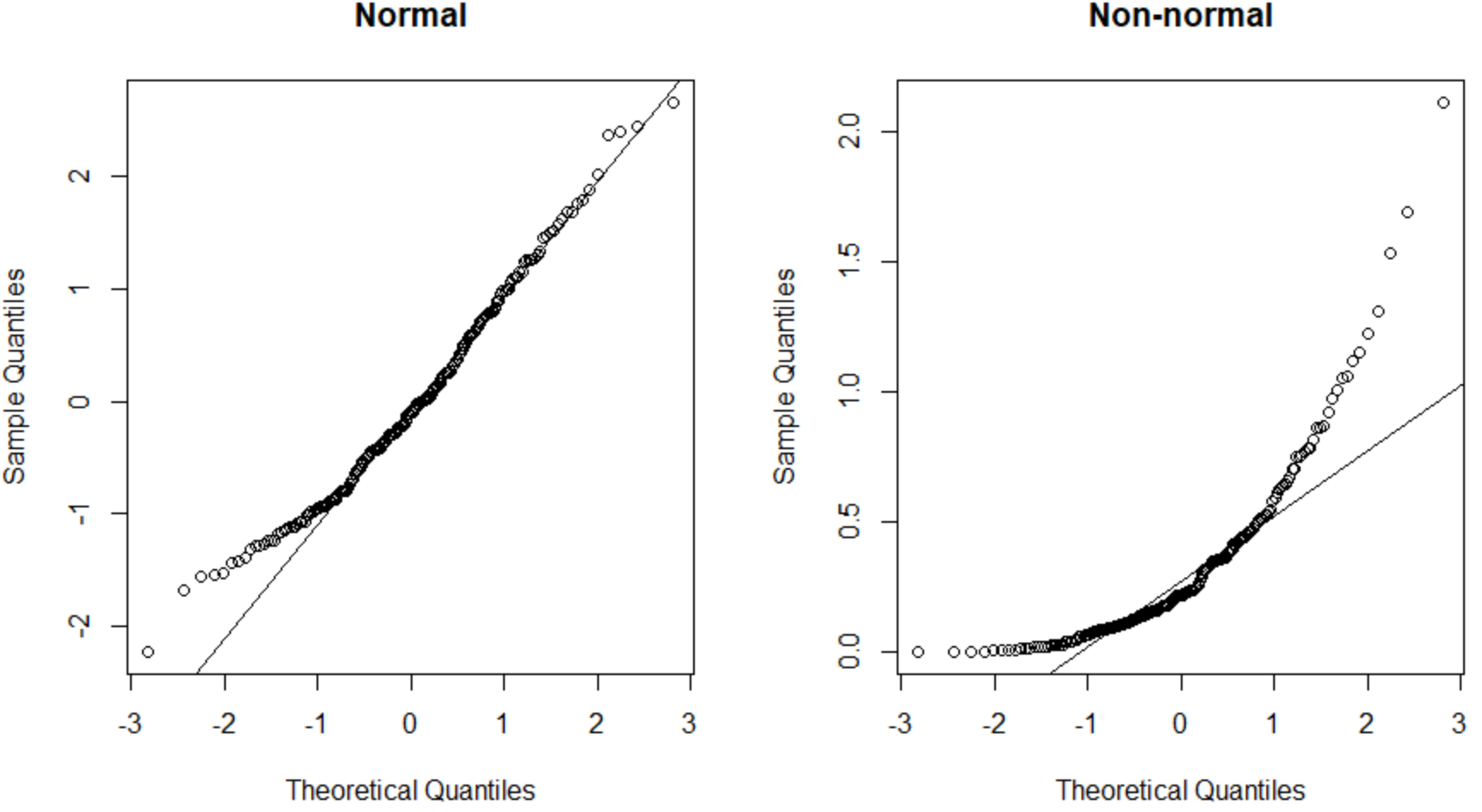
Das QQ-Diagramm auf der linken Seite stellt einen Datensatz dar, der normalverteilt ist (die Punkte fallen entlang einer geraden diagonalen Linie), und das QQ-Diagramm auf der rechten Seite zeigt einen Datensatz, der nicht normalverteilt ist.

Methode 3: Führen Sie einen Shapiro-Wilk-Test durch

Der folgende Code zeigt, wie man einen Shapiro-Wilk-Test für einen normalverteilten und nicht normalverteilten Datensatz in R durchführt:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

Der p-Wert des ersten Tests beträgt nicht weniger als 0,05, was darauf hinweist, dass die Daten normalverteilt sind.

Der p-Wert des zweiten Tests liegt unter 0,05, was darauf hinweist, dass die Daten nicht normalverteilt sind.

Methode 4: Führen Sie einen Kolmogorov-Smirnov-Test durch

Der folgende Code zeigt, wie ein Kolmogorov-Smirnov-Test für einen normalverteilten und nicht normalverteilten Datensatz in R durchgeführt wird:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

Der p-Wert des ersten Tests beträgt nicht weniger als 0,05, was darauf hinweist, dass die Daten normalverteilt sind.

Der p-Wert des zweiten Tests liegt unter 0,05, was darauf hinweist, dass die Daten nicht normalverteilt sind.

Umgang mit nicht normalen Daten

Wenn ein bestimmter Datensatz nicht normalverteilt ist , können wir häufig eine der folgenden Transformationen durchführen, um ihn normaler zu verteilen:

1. Log-Transformation: x-Werte in log(x) umwandeln.

2. Quadratwurzeltransformation: Transformieren Sie die Werte von x in √x .

3. Kubikwurzeltransformation: Transformieren Sie die Werte von x in x ^1/3 .

Durch die Durchführung dieser Transformationen wird der Datensatz im Allgemeinen normaler verteilt.

Lesen Siedieses Tutorial , um zu erfahren, wie Sie diese Transformationen in R durchführen.

Zusätzliche Ressourcen

So erstellen Sie Histogramme in R
So erstellen und interpretieren Sie ein QQ-Diagramm in R
So führen Sie einen Shapiro-Wilk-Test in R durch
So führen Sie einen Kolmogorov-Smirnov-Test in R durch