So testen sie die normalität in stata

Viele statistische Tests erfordern, dass eine oder mehrere Variablen normalverteilt sind, damit die Testergebnisse zuverlässig sind.

In diesem Tutorial werden verschiedene Methoden erläutert, mit denen Sie die Normalität zwischen Variablen in Stata testen können.

Für jede dieser Methoden verwenden wir den integrierten Stata-Datensatz namens auto . Sie können diesen Datensatz mit dem folgenden Befehl laden:

automatische Nutzung des Systems

Methode 1: Histogramme

Eine informelle Möglichkeit, festzustellen, ob eine Variable normalverteilt ist, besteht darin, ein Histogramm zu erstellen, um die Verteilung der Variablen anzuzeigen.

Wenn die Variable normalverteilt ist , sollte das Histogramm die Form einer „Glocke“ annehmen, wobei sich mehr Werte in der Nähe der Mitte und weniger Werte an den Enden befinden.

Mit dem Befehl hist können wir ein Histogramm für die variable Verschiebung erstellen:

bewegende Geschichte

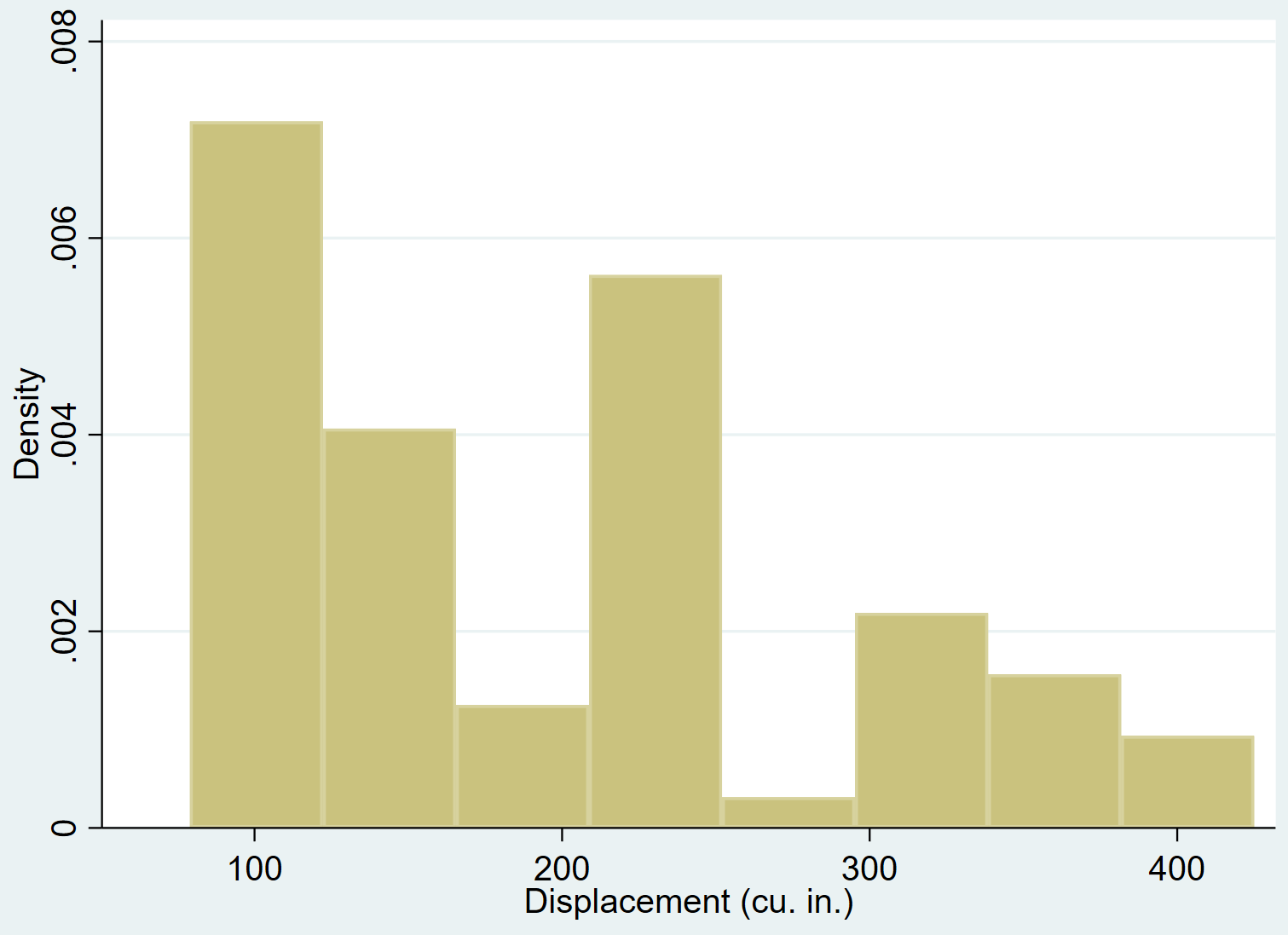
Mit dem normalen Befehl können wir einem Histogramm eine normale Dichtekurve hinzufügen:

bewegende Geschichte, normal

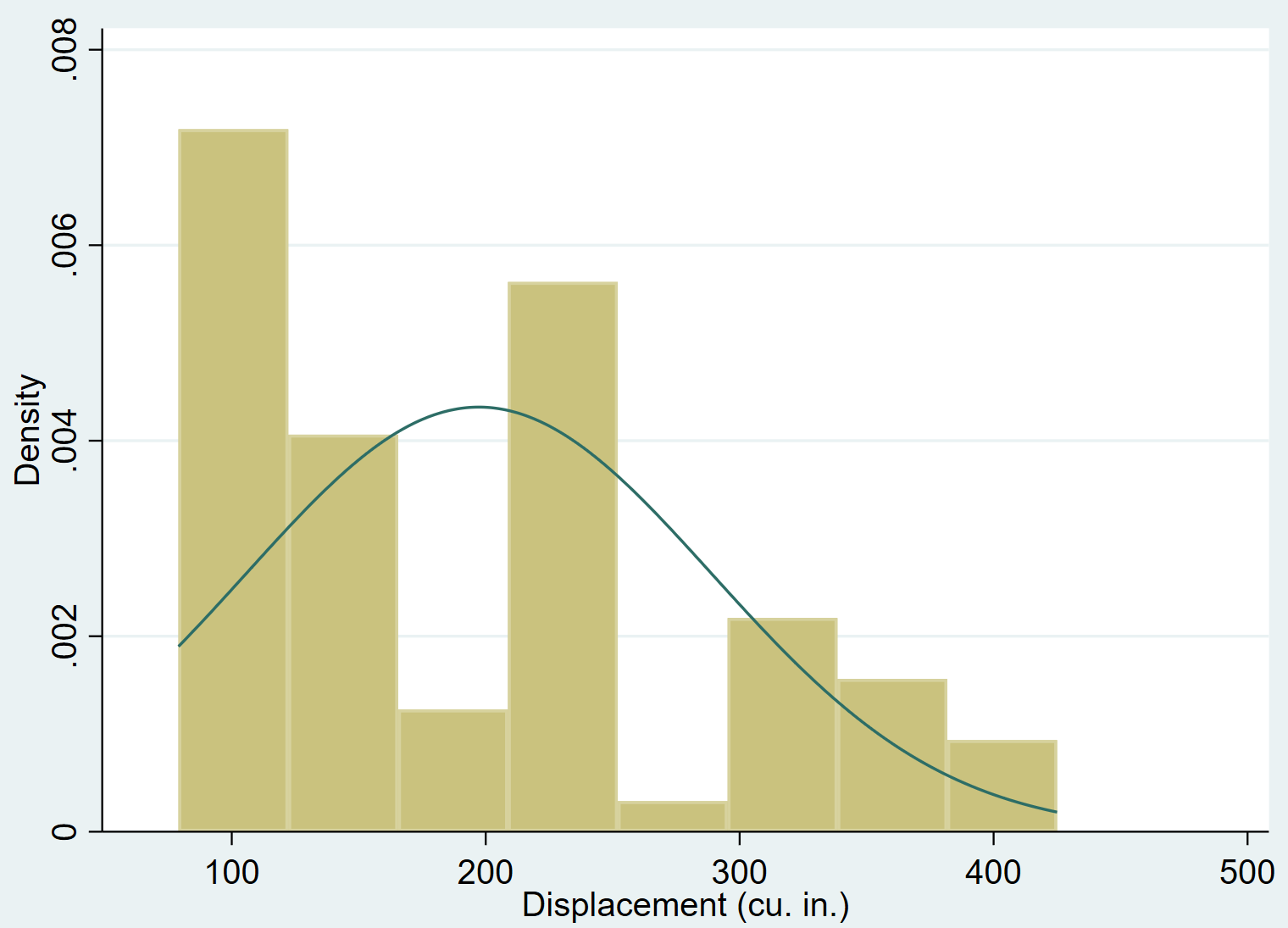
Es ist ziemlich offensichtlich, dass die Variablenverschiebung nach rechts verzerrt ist (z. B. sind die meisten Werte auf der linken Seite konzentriert und ein langer „Schwanz“ von Werten erstreckt sich nach rechts) und keiner Normalverteilung folgt.

Verwandte Themen: Links- und rechtsschiefe Verteilungen

Methode 2: Shapiro-Wilk-Test

Eine formale Möglichkeit, die Normalität zu testen, ist die Verwendung des Shapiro-Wilk-Tests .

Die Nullhypothese für diesen Test lautet, dass die Variable normalverteilt ist. Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (gängige Optionen sind 0,01, 0,05 und 0,10), können wir die Nullhypothese ablehnen und daraus schließen, dass genügend Beweise für die Behauptung vorliegen, dass die Variable nicht normalverteilt ist .

*Dieser Test kann verwendet werden, wenn die Gesamtzahl der Beobachtungen zwischen 4 und 2.000 liegt.

Mit dem Befehl swilk können wir einen Shapiro-Wilk-Test für die variable Verschiebung durchführen:

sanfte Bewegung

So interpretieren Sie das Testergebnis:

Obs: 74. Dies ist die Anzahl der im Test verwendeten Beobachtungen.

W: 0,92542. Dies ist die Teststatistik für den Test.

Prob>z: 0,00031. Dies ist der p-Wert, der der Teststatistik zugeordnet ist.

Da der p-Wert kleiner als 0,05 ist, können wir die Nullhypothese des Tests ablehnen. Wir haben genügend Beweise dafür, dass die variable Verschiebung nicht normalverteilt ist.

Wir können den Shapiro-Wilk-Test auch für mehrere Variablen gleichzeitig durchführen, indem wir mehrere Variablen nach dem Befehl swilk auflisten:

Swilk-Verdrängung, MPG-Länge

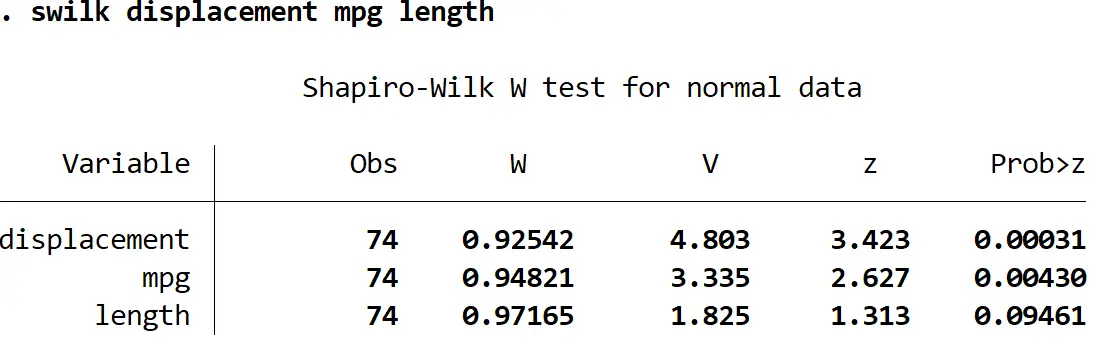
Bei einem Signifikanzniveau von 0,05 würden wir zu dem Schluss kommen, dass Verschiebung und mpg nicht normalverteilt sind, aber wir haben nicht genügend Beweise, um zu sagen, dass Länge nicht normalverteilt ist.

Methode 3: Shapiro-Francia-Test

Eine weitere formale Möglichkeit, die Normalität zu testen, ist die Verwendung des Shapiro-Francia-Tests .

Die Nullhypothese für diesen Test lautet, dass die Variable normalverteilt ist. Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt, können wir die Nullhypothese ablehnen und daraus schließen, dass genügend Beweise dafür vorliegen, dass die Variable nicht normalverteilt ist.

*Dieser Test kann verwendet werden, wenn die Gesamtzahl der Beobachtungen zwischen 10 und 5.000 liegt.

Mit dem Befehl sfrancia können wir einen Shapiro-Wilk-Test für die variable Verschiebung durchführen:

Sfrancia bewegen

So interpretieren Sie das Testergebnis:

Obs: 74. Dies ist die Anzahl der im Test verwendeten Beobachtungen.

W‘: 0,93011. Dies ist die Teststatistik für den Test.

Prob>z: 0,00094. Dies ist der p-Wert, der der Teststatistik zugeordnet ist.

Da der p-Wert kleiner als 0,05 ist, können wir die Nullhypothese des Tests ablehnen. Wir haben genügend Beweise dafür, dass die variable Verschiebung nicht normalverteilt ist.

Ähnlich wie beim Shapiro-Wilk-Test können Sie den Shapiro-Francia-Test für mehrere Variablen gleichzeitig durchführen, indem Sie mehrere Variablen nach dem Befehl sfrancia auflisten.

Methode 4: Schiefe- und Kurtosis-Test

Eine andere Möglichkeit, die Normalität zu testen, ist die Verwendung des Schiefe- und Kurtosis-Tests , der bestimmt, ob die Schiefe und Kurtosis einer Variablen mit der Normalverteilung übereinstimmen oder nicht.

Die Nullhypothese für diesen Test lautet, dass die Variable normalverteilt ist. Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt, können wir die Nullhypothese ablehnen und daraus schließen, dass genügend Beweise dafür vorliegen, dass die Variable nicht normalverteilt ist.

*Für diesen Test sind mindestens 8 Beobachtungen erforderlich.

Mit dem Befehl sktest können wir einen Schiefe- und Kurtosis-Test für die variable Verschiebung durchführen:

den Test verschieben

So interpretieren Sie das Testergebnis:

Obs: 74. Dies ist die Anzahl der im Test verwendeten Beobachtungen.

adj chi(2): 5,81. Dies ist die Chi-Quadrat-Teststatistik für den Test.

Prob>chi2: 0,0547. Dies ist der p-Wert, der der Teststatistik zugeordnet ist.

Da der p-Wert nicht kleiner als 0,05 ist, können wir die Nullhypothese des Tests nicht ablehnen. Wir haben nicht genügend Beweise, um zu sagen, dass Bewegungen nicht normalverteilt sind.

Ähnlich wie bei anderen Normalitätstests können Sie den Schiefe- und Kurtosis-Test für mehrere Variablen gleichzeitig durchführen, indem Sie mehrere Variablen nach dem Befehl sktest auflisten.