Normalverteilung

In diesem Artikel wird erklärt, was die Normalverteilung in der Statistik ist. Hier finden Sie die Definition der Normalverteilung, Beispiele für Normalverteilungen und die Eigenschaften der Normalverteilung.

Was ist die Normalverteilung?

Die Normalverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, deren Diagramm glockenförmig und symmetrisch um seinen Mittelwert ist. In der Statistik wird die Normalverteilung zur Modellierung von Phänomenen mit sehr unterschiedlichen Eigenschaften verwendet, weshalb diese Verteilung so wichtig ist.

Tatsächlich gilt die Normalverteilung in der Statistik als die mit Abstand wichtigste Verteilung aller Wahrscheinlichkeitsverteilungen, da sie nicht nur eine große Anzahl realer Phänomene modellieren kann, sondern die Normalverteilung auch zur Approximation anderer Arten von Phänomenen verwendet werden kann Verteilungen. unter bestimmten Bedingungen.

Das Symbol für die Normalverteilung ist der Großbuchstabe N. Um anzuzeigen, dass eine Variable einer Normalverteilung folgt, wird sie mit dem Buchstaben N gekennzeichnet und die Werte ihres arithmetischen Mittels und ihrer Standardabweichung werden in Klammern hinzugefügt.

Die Normalverteilung hat viele verschiedene Namen, einschließlich Gauß-Verteilung , Gauß-Verteilung und Laplace-Gauß-Verteilung .

Beispiele für Normalverteilungen

Normalerweise enthalten Datensätze, die einer Normalverteilung folgen, eine große Anzahl von Beobachtungen und decken sehr allgemeine Themen ab. Nachfolgend finden Sie einige Beispiele für statistische Stichproben, die im Allgemeinen mit einer Normalverteilung modelliert werden können.

Beispiele für Normalverteilung:

1. Die Größe der Studierenden in einem Kurs.
2. Der IQ der Mitarbeiter eines Unternehmens.
3. Die Anzahl der fehlerhaften Teile, die in einer Fabrik an einem Tag produziert werden.
4. Die Noten, die Studierende in einem Kurs bei einer Prüfung erhalten.
5. Die Rentabilität von Aktien börsennotierter Unternehmen.

Normalverteilungsdiagramm

Nachdem wir gesehen haben, was die Normalverteilung ist und einige Beispiele für diese Art von Wahrscheinlichkeitsverteilung, schauen wir uns an, wie ihr Diagramm aussieht, um das Konzept besser zu verstehen.

In der folgenden Grafik können Sie sehen, wie sich die Dichtefunktion der Normalverteilung in Abhängigkeit von den Werten ihres arithmetischen Mittels und ihrer Standardabweichung ändert.

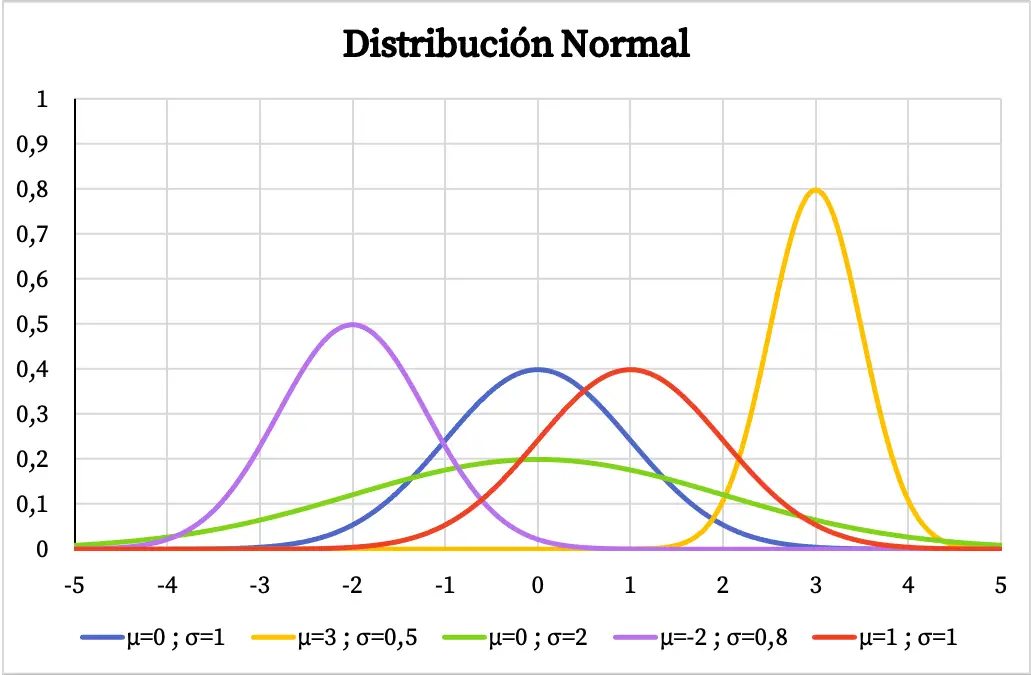
Wenn eine Variable normalverteilt ist und eine Glockenform aufweist, die auf dem arithmetischen Mittel zentriert ist, bedeutet dies, dass der am häufigsten wiederholte Wert der Mittelwert ist und dass sich Werte um den Mittelwert häufiger wiederholen als Extremwerte. Ebenso gilt: Je größer die Standardabweichung der Normalverteilung, desto flacher ist die Form ihrer grafischen Darstellung.

Andererseits hängt der Graph der kumulativen Wahrscheinlichkeitsfunktion der Normalverteilung auch von den Werten ihres arithmetischen Mittels und ihrer Standardabweichung ab, wie Sie im folgenden Bild sehen können:

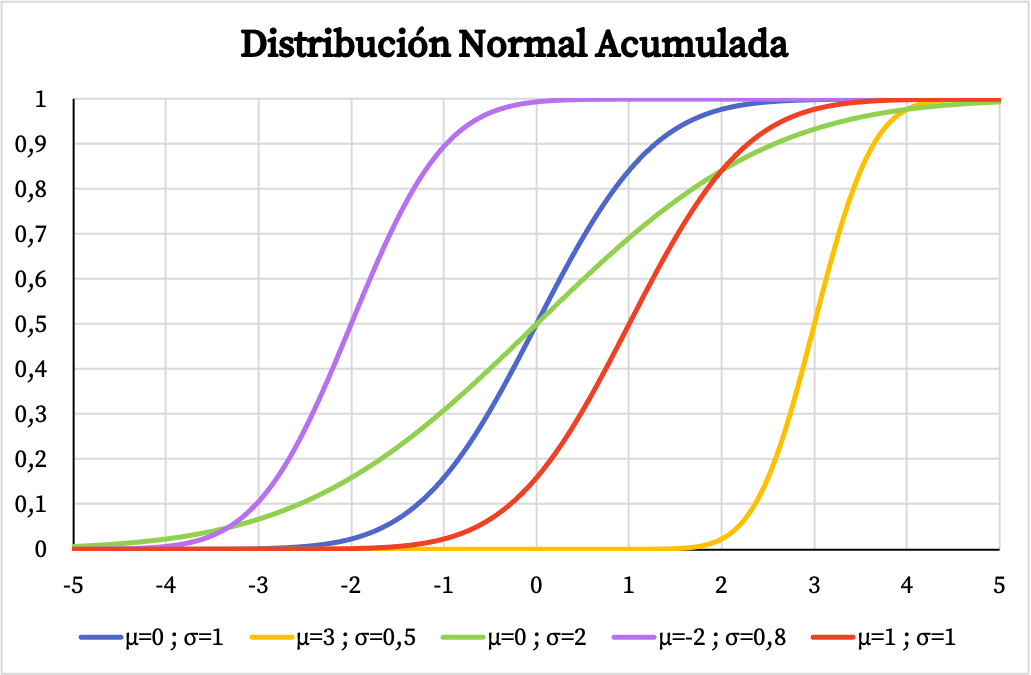
Die Dichtefunktion und die Verteilungsfunktion der Normalverteilung ermöglichen die Berechnung von Wahrscheinlichkeiten, die mit dieser Verteilung verknüpft sind. Anstatt jedoch deren Formeln zu verwenden, können Sie direkt die Normalverteilungstabellen verwenden, da diese schneller sind. Sie können diese Tabellen unter folgendem Link einsehen:

Merkmale der Normalverteilung

Die Normalverteilung weist folgende Merkmale auf:

• Die Normalverteilung hängt von zwei charakteristischen Parametern ab, nämlich ihrem arithmetischen Mittel (μ) und ihrer Standardabweichung (σ).

• Die Normalverteilung kann positive und negative Werte annehmen, sodass der Bereich der Normalverteilung aus reellen Zahlen besteht.

• Der Median und der Modus der Normalverteilung entsprechen dem arithmetischen Mittel der Verteilung.

• Der Schiefekoeffizient und der Kurtosiskoeffizient der Normalverteilung sind Null.

• Die Formel für die Dichtefunktion der Normalverteilung lautet:

• Ebenso lautet die Formel für die kumulative Wahrscheinlichkeitsfunktion der Normalverteilung:

• Eine Anwendung des zentralen Grenzwertsatzes besteht darin, dass eine Poisson-Verteilung eine Normalverteilung annähern kann, wenn der Wert von λ ausreichend groß ist.

• Eine weitere Anwendung des zentralen Grenzwertsatzes besteht darin, dass eine Binomialverteilung für Datensätze mit einer großen Anzahl von Beobachtungen durch eine Normalverteilung angenähert werden kann.

Standardnormalverteilung

Die Standardnormalverteilung , auch Einheitsnormalverteilung genannt, ist der einfachste Fall einer Normalverteilung. Genauer gesagt ist die Standardnormalverteilung eine Normalverteilung mit Mittelwert und Standardabweichungswert gleich 0 bzw. 1.

Beachten Sie, dass jede Normalverteilung in eine Standardnormalverteilung umgewandelt werden kann, indem man einen Prozess namens Typisierung anwendet, bei dem von jedem Wert sein arithmetisches Mittel subtrahiert und dann durch seine Standardabweichung dividiert wird.

Darüber hinaus wird die Standardnormalverteilung verwendet, um anhand ihrer Wahrscheinlichkeitstabelle die Wahrscheinlichkeit einer Normalverteilung zu bestimmen. Um also die Wahrscheinlichkeit einer Normalverteilung zu ermitteln, wird zunächst die Variable eingegeben, um sie in eine Standardnormalverteilung umzuwandeln. Anschließend schauen wir in der Tabelle nach, wie hoch der entsprechende Wahrscheinlichkeitswert ist. Um mehr zu erfahren, klicken Sie auf den folgenden Link:

Die Normalverteilung und die empirische Regel

In der Statistik ist die Faustregel , auch 68-95-99,7-Regel genannt, eine Regel, die den Prozentsatz der Werte in einer Normalverteilung definiert, die innerhalb von drei Standardabweichungen vom Mittelwert liegen.

Im Einzelnen besagt die Faustregel Folgendes:

• 68 % der Werte einer Normalverteilung liegen innerhalb einer Standardabweichung vom Mittelwert.
• 95 % der Werte einer Normalverteilung liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
• 99,7 % der Werte in einer Normalverteilung liegen innerhalb von drei Standardabweichungen vom Mittelwert.