Normalverteilung und t-verteilung: was ist der unterschied?

DieNormalverteilung ist die in allen Statistiken am häufigsten verwendete Verteilung und bekanntermaßen symmetrisch und glockenförmig.

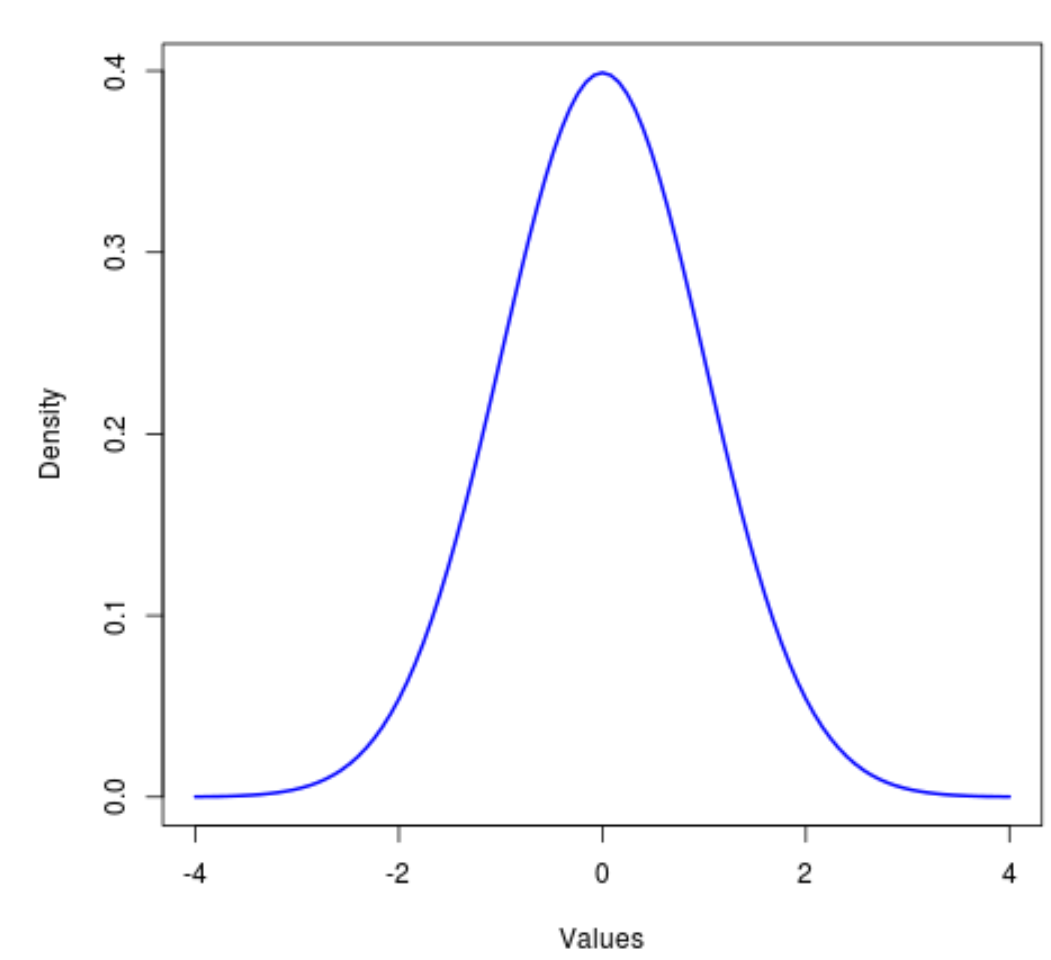
Eine eng verwandte Verteilung ist die t-Verteilung , die ebenfalls symmetrisch und glockenförmig ist, aber schwerere „Schwänze“ als die Normalverteilung aufweist.

Mit anderen Worten: Im Vergleich zur Normalverteilung befinden sich in der Verteilung mehr Werte an den Enden als in der Mitte:

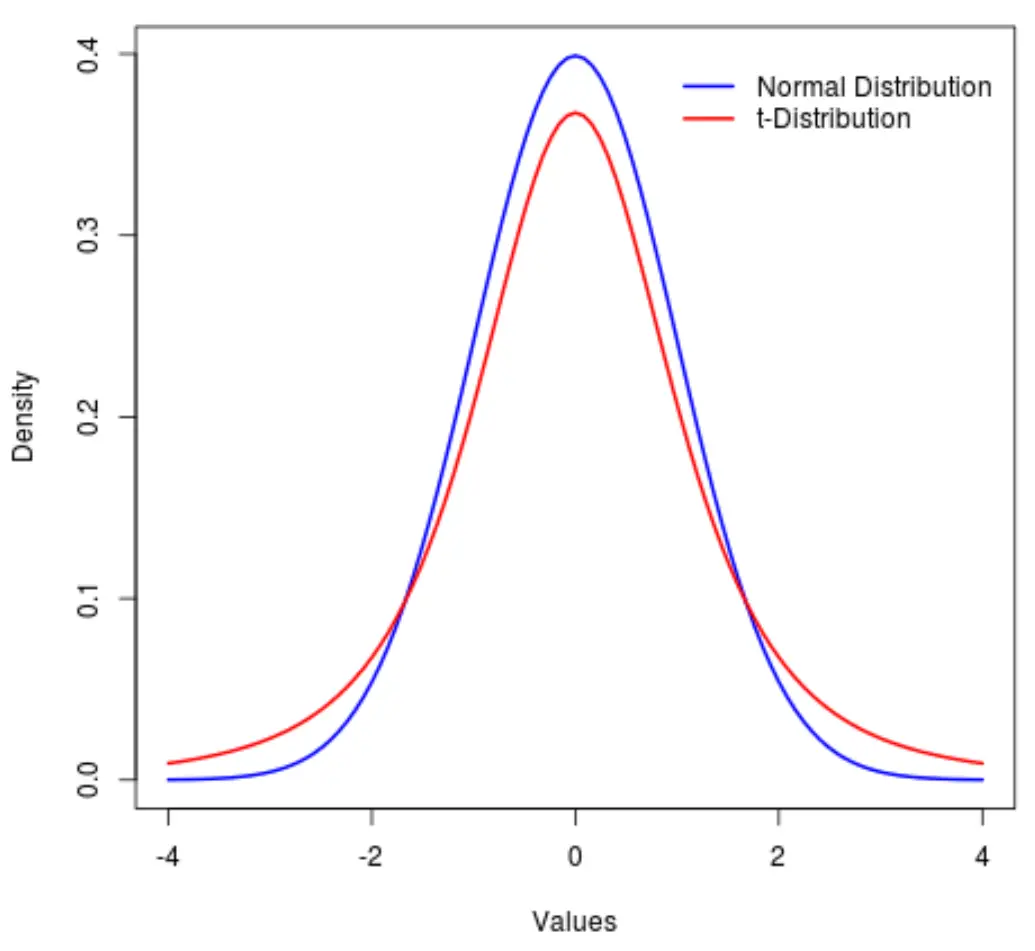
Im statistischen Fachjargon verwenden wir eine Metrik namens Kurtosis , um zu messen, wie „schwer“ eine Verteilung ist. Wir würden also sagen, dass die Kurtosis einer t-Verteilung größer ist als die einer Normalverteilung.

In der Praxis verwenden wir am häufigsten die t-Verteilung, wenn wir Hypothesentests durchführen oderKonfidenzintervalle erstellen .

Die Formel zur Berechnung eines Konfidenzintervalls für einen Grundgesamtheitsmittelwert lautet beispielsweise:

Konfidenzintervall = x +/- t _{1-α/2, n-1} *(s/√ n )

Gold:

• x : Stichprobenmittelwert
• t: der kritische t-Wert, basierend auf dem Signifikanzniveau α und der Stichprobengröße n
• s: Stichprobenstandardabweichung
• n: Stichprobengröße

In dieser Formel verwenden wir den kritischen Wert von Tabelle t anstelle des kritischen Werts von Tabelle z, wenn eine der folgenden Bedingungen zutrifft:

• Wir kennen die Populationsstandardabweichung nicht.
• Die Stichprobengröße ist kleiner oder gleich 30.

Das folgende Flussdiagramm bietet eine nützliche Möglichkeit herauszufinden, ob Sie den kritischen Wert aus Tabelle t oder Tabelle z verwenden sollten:

Der Hauptunterschied zwischen der Verwendung der t-Verteilung und der Verwendung der Normalverteilung bei der Konstruktion von Konfidenzintervallen besteht darin, dass die kritischen Werte der t-Verteilung größer sind, was zu breiteren Konfidenzintervallen führt.

Angenommen, wir möchten ein 95-%-Konfidenzintervall für das Durchschnittsgewicht einer Schildkrötenpopulation erstellen, um eine Zufallsstichprobe von Schildkröten mit den folgenden Informationen zu sammeln:

• Stichprobengröße n = 25
• Durchschnittliches Probengewicht x = 300
• Stichprobenstandardabweichung s = 18,5

Der kritische z-Wert für ein 95 %-Konfidenzintervall beträgt 1,96 , während ein kritischer t-Wert für ein 95 %-Konfidenzintervall mit df = 25-1 = 24 Freiheitsgraden 2,0639 beträgt.

Somit ist ein 95 %-Konfidenzintervall für den Grundgesamtheitsmittelwert unter Verwendung eines z-kritischen Werts:

95 % KI = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]

Während ein 95 %-Konfidenzintervall für den Grundgesamtheitsmittelwert unter Verwendung eines t-kritischen Werts lautet:

95 % KI = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]

Beachten Sie, dass das Konfidenzintervall mit dem t-kritischen Wert breiter ist.

Der Grundgedanke dabei ist, dass wir bei kleinen Stichprobengrößen weniger sicher sind, was der wahre Mittelwert der Grundgesamtheit ist. Daher ist es sinnvoll, die t-Verteilung zu verwenden, um breitere Konfidenzintervalle zu erzeugen, die mit größerer Wahrscheinlichkeit den wahren Mittelwert der Grundgesamtheit enthalten.

Visualisierung der Freiheitsgrade für die t-Verteilung

Es ist zu beachten, dass sich die t-Verteilung mit zunehmenden Freiheitsgraden der Normalverteilung annähert.

Betrachten Sie zur Veranschaulichung die folgende Grafik, die die Form der t-Verteilung mit den folgenden Freiheitsgraden zeigt:

• df = 3
• df = 10
• df = 30

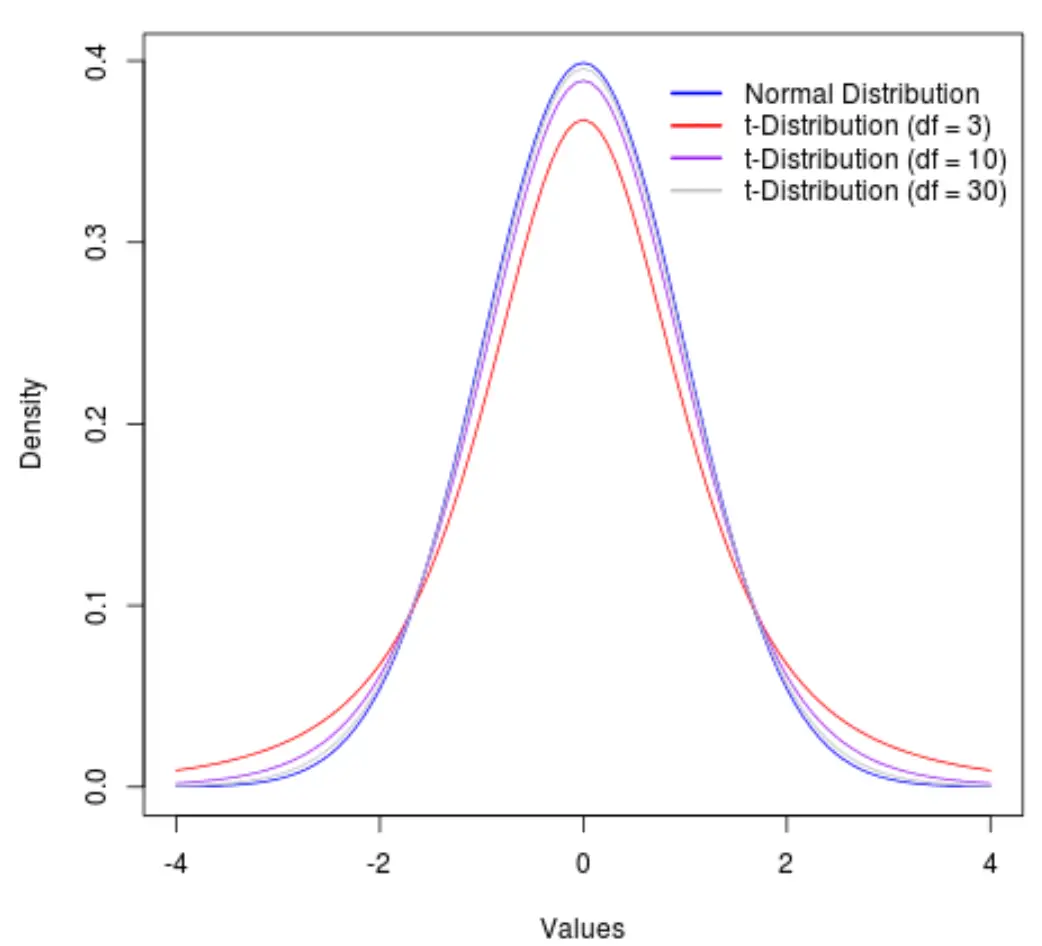
Über 30 Freiheitsgrade hinaus werden die t-Verteilung und die Normalverteilung so ähnlich, dass die Unterschiede zwischen der Verwendung eines t-kritischen Werts und eines z-kritischen Werts in den Formeln vernachlässigbar werden.