Normalverteilung und standardnormalverteilung: der unterschied

Die Normalverteilung ist die in der Statistik am häufigsten verwendete Wahrscheinlichkeitsverteilung.

Es hat die folgenden Eigenschaften:

• Symmetrisch
• Glockenförmig
• Der Mittelwert und der Median sind gleich; beide liegen im Zentrum der Verteilung

Der Mittelwert der Normalverteilung bestimmt ihren Standort und die Standardabweichung bestimmt ihre Streuung.

Die folgende Grafik zeigt beispielsweise drei Normalverteilungen mit unterschiedlichen Mittelwerten und Standardabweichungen:

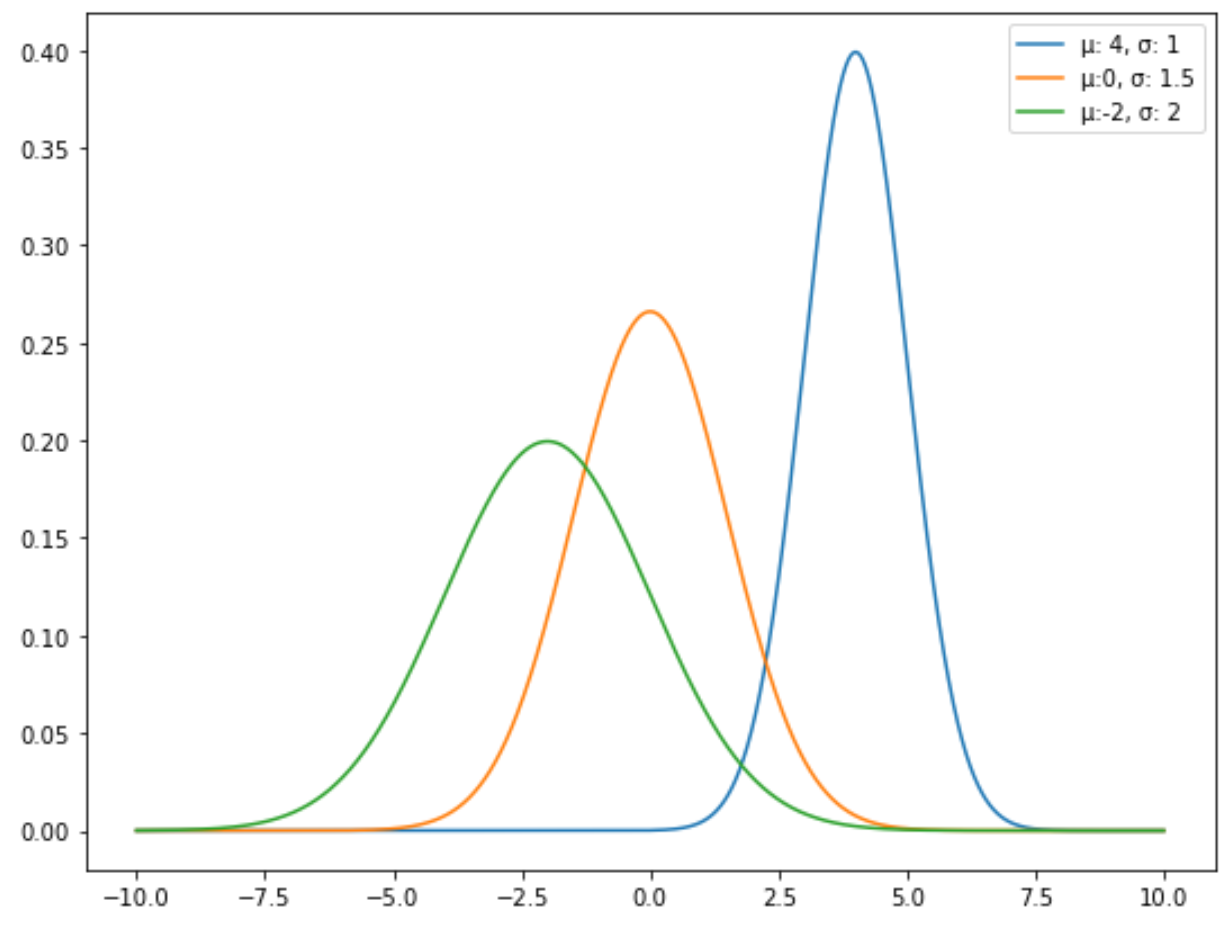
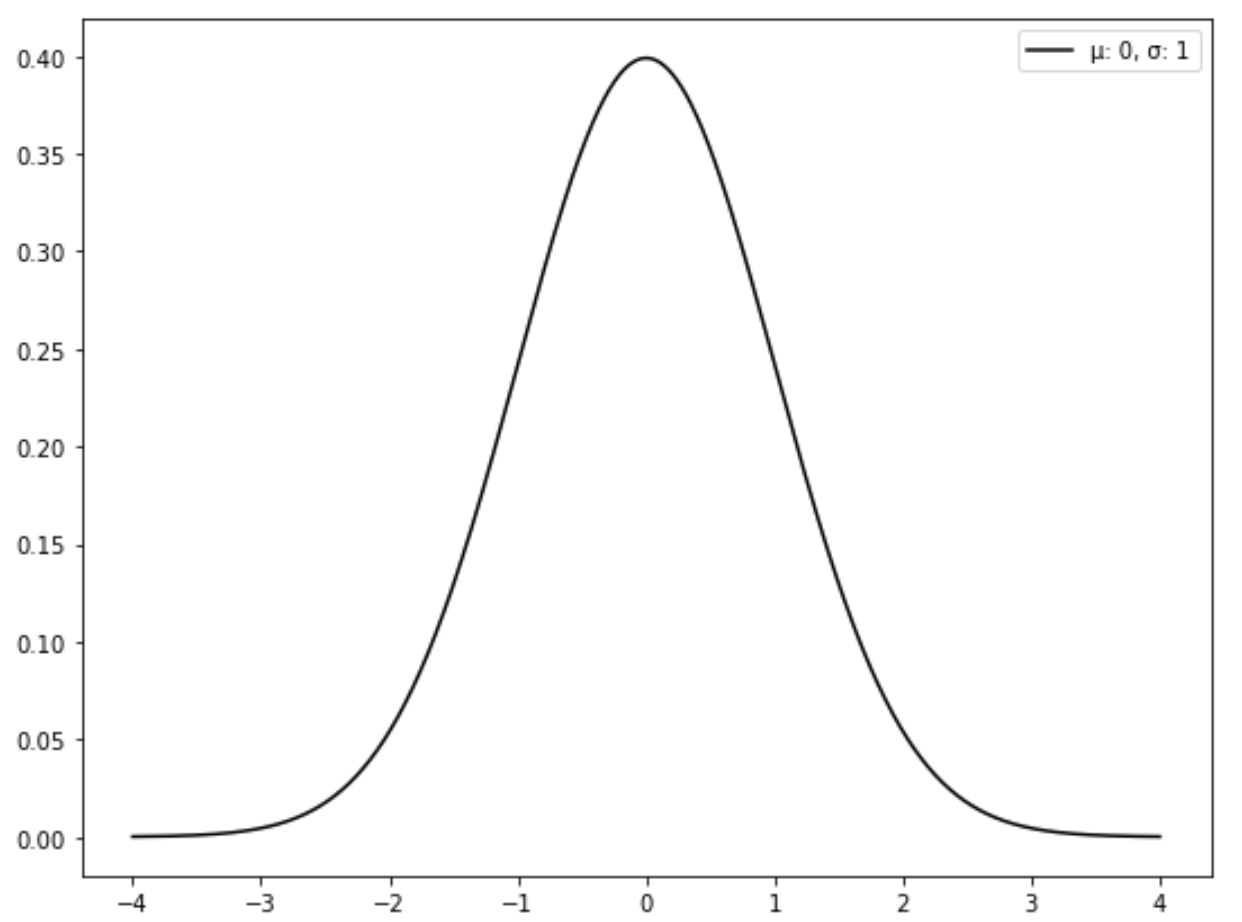
Die Standardnormalverteilung ist eine spezielle Art der Normalverteilung, bei der der Mittelwert 0 und die Standardabweichung 1 beträgt.

Die folgende Grafik zeigt eine Standardnormalverteilung:

So konvertieren Sie eine Normalverteilung in eine Standardnormalverteilung

Jede Normalverteilung kann in eine Standardnormalverteilung umgewandelt werden, indem die Datenwerte mithilfe der folgenden Formel in Z-Scores umgewandelt werden:

z = (x – μ) / σ

Gold:

• x: Wert der einzelnen Daten
• μ: Mittelwert der Verteilung
• σ: Standardabweichung der Verteilung

Angenommen, wir haben den folgenden Datensatz mit einem Mittelwert von 6 und einer Standardabweichung von 2,152:

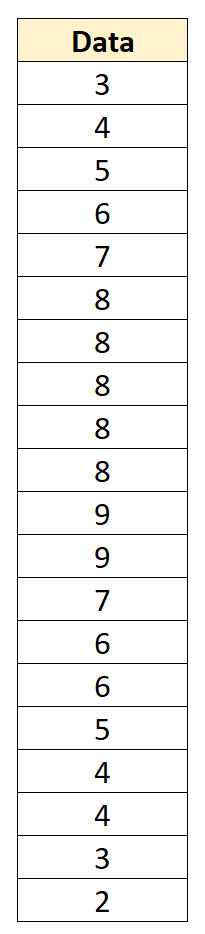
Wir können jeden einzelnen Datenwert in einen Z-Score umwandeln, indem wir von jedem Wert 6 subtrahieren und durch 2,152 dividieren:

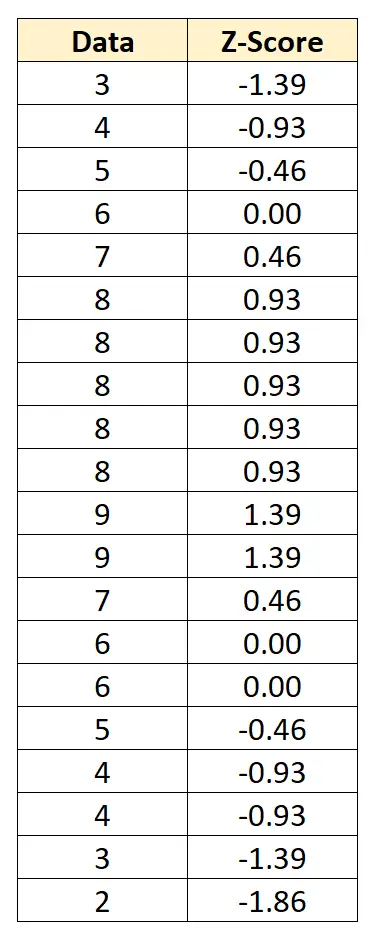
Der Z-Score sagt uns, wie viele Standardabweichungen jeder Datenpunkt vom Mittelwert hat. Beispielsweise liegt der erste Datenwert „3“ 1,39 Standardabweichungen unter dem Mittelwert.

Der Mittelwert dieser Bewertungsverteilung hat einen Mittelwert von Null und eine Standardabweichung von Eins.

So verwenden Sie die Standardnormalverteilung

Eine Standardnormalverteilung hat die folgenden Eigenschaften:

• Etwa 68 % der Daten liegen innerhalb einer Standardabweichung vom Mittelwert
• Etwa 95 % der Daten liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
• Etwa 99,7 % der Daten liegen innerhalb von drei Standardabweichungen vom Mittelwert.

Dies wird als Faustregel bezeichnet und dient dazu, die Verteilung von Werten in einem Datensatz zu verstehen.

Nehmen wir beispielsweise an, dass die Höhe der Pflanzen in einem bestimmten Garten normalverteilt ist und einen Mittelwert von 47,4 Zoll und eine Standardabweichung von 2,4 Zoll aufweist.

Wie viel Prozent der Pflanzen sind nach der Faustregel weniger als 54,6 Zoll hoch?

Die Faustregel besagt, dass bei einem gegebenen Datensatz mit Normalverteilung 99,7 % der Datenwerte innerhalb von drei Standardabweichungen vom Mittelwert liegen. Das bedeutet, dass 49,85 % der Werte zwischen dem Mittelwert und drei Standardabweichungen über dem Mittelwert liegen.

In diesem Beispiel liegt 54,6 drei Standardabweichungen über dem Mittelwert. Da wir wissen, dass 50 % der Datenwerte kleiner als der Mittelwert einer Normalverteilung sind, sind insgesamt 50 % + 49,85 % = 99,85 % der Werte kleiner als 54,6.

99,85 % der Pflanzen sind also weniger als 54,6 Zoll groß.

Zusätzliche Ressourcen

Probleme bei der Anwendung von Faustregeln
Faustregelrechner
So wenden Sie die Faustregel in Excel an